Finance

发布日期: 2023-07-14

作者: Frank Yu

文章字数: 23.4k

阅读时长: 90 分

阅读次数:

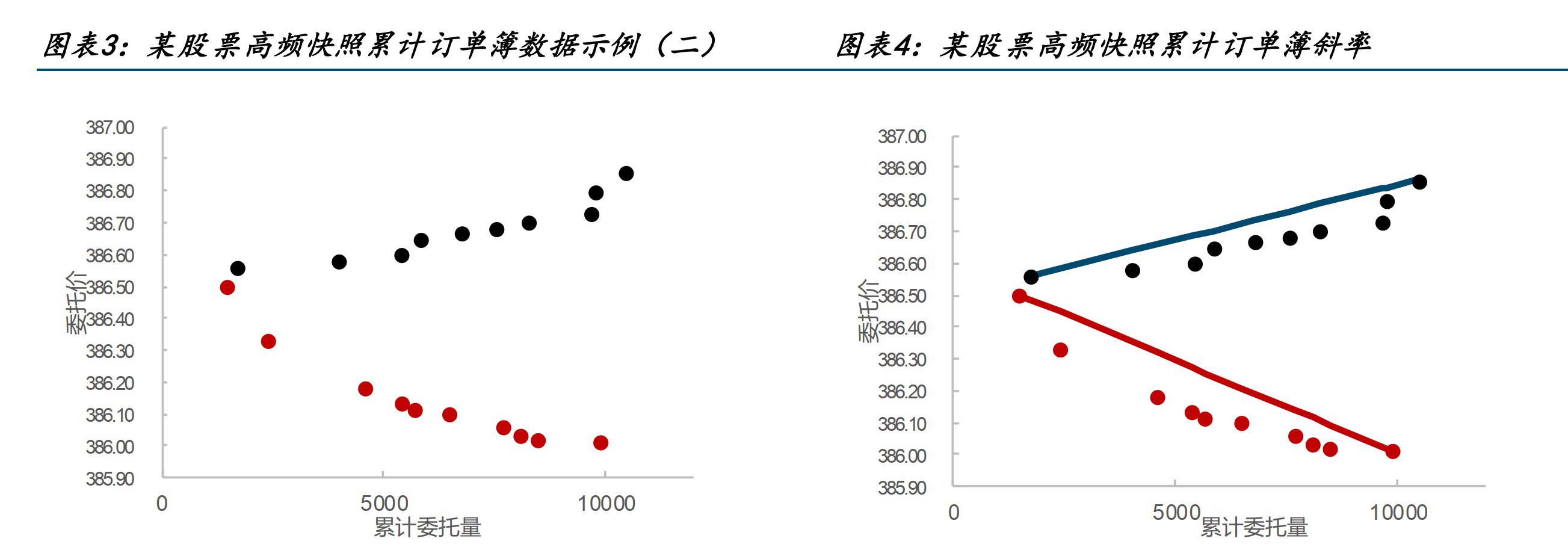
一. 统计量类

1. 已实现方差 real_var（Concerned）

因子构造

$$\text { real_var }{D, i}=\frac{1}{T-2} \sum{t=2}^T(r_{t, D, i}-\bar{r}_{D, i})^2$$
个股 i 在D日的日内分钟频率下的股票收益率序列为 $r_{t,D,i}$, 股票价格序列为 $P_{t,D,i}$
$$r_{t,D,i}=\frac{P_{t,D,i}}{P_{t-1,D,i}}-1$$

因子说明

分钟行情收益率的方差
数据：分钟K线

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

T的不同取值

注释

直接使用pandas var（）函数，return乘了100

2. 已实现偏度 real_skew（Concerned）

因子构造

$$real_skew_{D,i}=\frac{1}{T-1} \sum_{t=2}^T\frac{(r_{t, D, i}-\bar{r}{D, i})^3}{\text{real_var}{D, i}^{3/2}}$$

个股 i 在D日的日内分钟频率下的股票收益率序列为 $r_{t,D,i}$, 股票价格序列为 $P_{t,D,i}$
- $$r_{t,D,i}=\frac{P_{t,D,i}}{P_{t-1,D,i}}-1$$
$\bar{r}_{D,i}$ 表示股票日内收益率的均值
$$\text { real_var }{D, i}=\frac{1}{T-2} \sum{t=2}^T(r_{t, D, i}-\bar{r}_{D, i})^2$$

因子说明

收益率偏度可以用来度量收益率分布的不对称性，取值范围为(−∞, +∞)，当偏度<0时，表示收益率分布左偏，当偏度>0时，表示收益率分布右偏。
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

T的不同取值

注释

直接使用pandas skew（）函数，return乘了100.

3. 已实现峰度 real_kurtosis（Concerned）

因子构造

$$\text { real_kurtosis }{D, i}=\frac{1}{T-1} \sum{t=2}^T \frac{\left(r_{t, D, i}-\bar{r}{D, i}\right)^4}{\text { real_var }{D, i}{ }^2}$$

个股 i 在D日的日内分钟频率下的股票收益率序列为 $r_{t,D,i}$, 股票价格序列为 $P_{t,D,i}$
- $$r_{t,D,i}=\frac{P_{t,D,i}}{P_{t-1,D,i}}-1$$
$\bar{r}_{D,i}$ 表示股票日内收益率的均值
$$\text { real_var }{D, i}=\frac{1}{T-2} \sum{t=2}^T(r_{t, D, i}-\bar{r}_{D, i})^2$$

因子说明

峰度可以用来度量随机变量概率分布的陡峭程度。收益率峰度取值范围为[1, +∞)，当峰度超过3时，认为该分布厚尾。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

T的不同取值

注释

直接使用pandas kurtosis函数，return乘了100

4. 上行收益率方差 real_upvar（Concerned）

因子构造

仅考虑收益率大于 0 时的分钟行情收益率方差
$$\text { real_var }{D, i}=\frac{1}{T-2} \sum{t=2}^T(r_{t, D, i}-\bar{r}_{D, i})^2$$
个股 i 在D日的日内分钟频率下的股票收益率序列为 $r_{t,D,i}$, 股票价格序列为 $P_{t,D,i}$
- $$r_{t,D,i}=\frac{P_{t,D,i}}{P_{t-1,D,i}}-1$$

因子说明

real_var的一部分

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

T的不同取值

注释

return乘了100

5. 下行收益率方差 real_downvar（Concerned）

因子构造

仅考虑收益率小于 0 时的分钟行情收益率方差
$$\text { real_var }{D, i}=\frac{1}{T-2} \sum{t=2}^T(r_{t, D, i}-\bar{r}_{D, i})^2$$
个股 i 在D日的日内分钟频率下的股票收益率序列为 $r_{t,D,i}$, 股票价格序列为 $P_{t,D,i}$
- $$r_{t,D,i}=\frac{P_{t,D,i}}{P_{t-1,D,i}}-1$$

因子说明

real_var的一部分

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

T的不同取值

注释

return乘了100

6. 上行收益率方差比值 ratio_realupvar（Concerned）

因子构造

$$\text { ratio_realupvar }{D, i}=\frac{\text { real_upvar }{D, i}}{\text { real_var }_{D, i}}$$

分子和分母见上。

因子说明

上行收益率方差占比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

T的不同取值

7. 下行收益率方差比值 ratio_realdownvar（Concerned）

因子构造

$$\text { ratio_realdownvar }{D, i}=\frac{\text { real_downvar }{D, i}}{\text { real_var }_{D, i}}$$

分子和分母见上。

因子说明

下行收益率方差占比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

8. 开盘后半小时real_skew real_skewH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

使用skew（），return乘了100

9. 开盘后半小时real_kurtosis real_kurtosisH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

return乘了100

10. 开盘后半小时real_var real_varH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

return乘了100

11. 收盘前半小时real_var real_varH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

收盘时段，14：57 后是否保留

注释

return乘了100

12. 收盘前半小时real_skew real_skewH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

收盘时段，14：57 后是否保留

注释

return乘了100

13. 收盘前半小时real_kurtosis real_kurtosisH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

收盘时段，14：57 后是否保留

注释

return乘了100

14. 大成交量已实现偏度 real_skewlarge（Good）

因子构造

$$\text { real_skewlarge }{D, i}=\frac{1}{T-1} \sum{t=2}^T \frac{\left(r_{t, D, i}-\bar{r}{D, i}\right)^3}{\text { real_var }{D, i}{ }^{3 / 2}}$$

将个股在每个交易日的分钟成交量时间序列按照成交量大小排序，将分钟成交量排名前1/3的成交量定义为“大成交量”。对这些按照skew公式计算偏度。

因子说明

在不同的成交中，大单成交与主力资金关联较大，蕴含的信息可能更多。
针对大成交量对应的时刻的股价信息，可以构建大成交量相关因子
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

return乘了100

15. 日度改进波动率 𝑅𝑒𝑡𝑢𝑟𝑛_𝑆𝑡𝑑_𝐼𝑚𝑝_𝐷（Good）

因子构造

$$\text { Return_Std_Imp_D}{i, T}(\text { 日度 })=-\sqrt{\sum{r_{i, t, T} \in r_{i, v o l_{up}, T}} \frac{(r_{i, t, T}-r_{i, m e a n, T})^2}{|r_{i, v o l_{u p}, T}|}} $$

其中 $r_{i, t, T}$ 为第 $\mathrm{i}$ 只股票在 $\mathrm{T}$ 日第 $\mathrm{t}$ 分钟的收益率,
$\left|r_{i, v o l_{u p}, T}\right|$ 定义为集合 $r_{i, v o l_{u p,}, T}$ 的基数,
放量时段 $\operatorname{vol}_{u p, i, T}$ 定义为 $\mathrm{T}$ 日分钟成交量均值加分钟成交量标准差, 当第 $\mathrm{t}$ 分钟成交量大于分钟成交量均值加分钟成交量标准差时, 将第 $\mathrm{t}$ 分钟定义为放量时段，当全天没有属于放量且大于 0 的收益分钟线, 则从当天的样本池中剔除该股票.
具体计算方法如下：
$$r_{i, v o l_{u p}, T}={r_{i, t, T} \mid v o l_{i, t, T} \in v_{u p}^{u p, i, T}}, \quad r_{i, \text { mean }, T}=\frac{\sum r_{i, v o l_{u p}, T}}{|r_{i, v o l_{u p}, T}|}$$

$$v_{u p, i, T}={v o l_{i, t, T} \mid v o l_{i, t, T}>v_u l_{m e a n, i, T}+v o l_{s t d, i, T}}$$

$$\operatorname{vol}{\text{mean,}i}=\frac{1}{240} \sum{j=1}^{j=240}\operatorname{vol}{i, j}$$
$$\operatorname{vol}{\text {std,i }}=\sqrt{\frac{1}{240} \sum_{j=1}^{j=240}(vol_{i, j}-{vol}_{m e a n, i})^2}$$

因子说明

量价数据，波动率

参考文献

2023-02-12_信达证券_信达金工指数增强系列报告之三：基于基金持仓、特色基本面因子以及高频价量因子的1000指数增强

注释

return乘了100

16. 中间价变化率 Midpoint Price Change, MPC（Concerned）

因子构造

$$M P C_{t, k}=\frac{M_t-M_{t-k}}{M_{t-k}}$$

其中，$$M_t=\frac{P_t^B+P_t^A}{2}$$

因子说明

MPC 因子衡量的是市场中间价的短期变动趋势，该趋势刻画了市场交易者的最新交易和挂单撤单行为，反应了市场交易者对股票价格未来走势的最新预期。
$𝑃𝑡^𝐵$ 和$𝑃_𝑡^𝐴$ 分别为 t 时刻的买一价和卖一价，市场中间价$𝑀_𝑡$ 为买一价和卖一价的平均值。$𝑀{𝑡−𝑘}$ 代表 k 分钟前的中间价，k 分别取 k = 1, 5，$𝑀𝑃𝐶_{𝑡,𝑘}$ 代表从时刻 t-k 到时刻 t 中间价$𝑀_𝑡$ 的百分比变化率。
数据：盘口数据

参考文献

中信建投-20210129-因子深度研究系列：高频订单失衡及价差因子

注意事项

盘口数据每3秒一档。因子频率，及其低频化方法

注释

此项为分钟频数据，低频化方法是17与18，因此本次构造没有构造本因子

17. 分钟频MPC的日频最大值, MPCmax（Concerned）

因子构造

$$M P Cmax_{d, k}=\max \left{M P C_{d, t, k}, t=k+1, \ldots, N_d\right}$$

其中，$$M P C_{d, t, k}=\frac{M_{d, t}-M_{d, t-k}}{M_{d, t-k}}$$
- $$M P C_{t, k}=\frac{M_t-M_{t-k}}{M_{t-k}}$$
- $$M_t=\frac{P_t^B+P_t^A}{2}$$
$𝑀𝑃𝐶𝑚𝑎𝑥_{𝑑,𝑘}$ 为日期 d 当天分钟频$𝑀𝑃𝐶_{𝑡,𝑘}$ 因子的最大值， $𝑀𝑃𝐶_{𝑑,𝑡,𝑘}$ 代表日期 d 的 t 时刻的$𝑀𝑃𝐶_{𝑡,𝑘}$ 因子， $𝑁_𝑑$ 代表日期 d 的交易分钟数。

因子说明

直接描述了中间价的最大变动幅度，MPCmax 越大，则股票长期下跌的概率越大

参考文献

中信建投-20210129-因子深度研究系列：高频订单失衡及价差因子

注意事项

盘口数据每3秒一档。因子频率，及其低频化方法

注释

取k=1

18. 分钟频MPC的日频偏度, MPCskew（Concerned）

因子构造

$$\text { MPCskew }{d, k}=\frac{1}{N_d-k-1} \sum{t=k+1}^{N_d}\left(\frac{M P C_{d, t, k}-\overline{M P C_{d, t, k}}}{\sigma_{d, t, k}}\right)^3$$

$𝑀𝑃𝐶𝑠𝑘𝑒𝑤_{𝑑,𝑘}$ 为日期 d 当天分钟频$𝑀𝑃𝐶_{𝑡,𝑘}$ 因子的偏度，$\overline{MPC_{d,t,k}}$ 代表日期 d 当天分钟频$𝑀𝑃𝐶_{𝑡,𝑘}$ 因子的平均值，$𝜎_{𝑑,𝑡,𝑘}$ 代表日期 d 当天分钟频$𝑀𝑃𝐶_{𝑡,𝑘}$ 因子的标准差

因子说明

描述了中间价的极端变动偏离平均值的幅度。MPCskew 越大，则股票长期下跌的概率越大

参考文献

中信建投-20210129-因子深度研究系列：高频订单失衡及价差因子

注意事项

盘口数据每3秒一档。因子频率，及其低频化方法

注释

取k=1

19. 分位数因子 QUA（Good）

因子构造

$$S= (A_{10%}-A_{min})/(A_{max}-A_{min})$$

逐个交易日回顾分钟单笔成交金额序列，记为 A；
将 A 从小到大排序，剔除最大的 10 个样本值（极端值）；
构造S，其中$𝐴_{𝑚𝑎𝑥}$、 $𝐴_{𝑚𝑖𝑛}$ 分别为最大和最小值， $𝐴_{10%}$ 为 10%分位值；
滚动 20 个交易日计算 S 指标的均值，即可得到 QUA 因子。

因子说明

成交金额序列相关
QUA 因子的 Alpha 来源可以理解为：大单相对小单的成交金额偏离越大，说明主力（“相对大单”）对于该股票的关注度越高，未来股价表现会越好。

参考文献

2022-06-12_开源证券_金融工程_市场微观结构研究系列（15）：高频因子：分钟单笔金额序列中的主力行为刻画

注意事项

不进行滚动20日平滑，也可构造1个因子

注释

未进行20日平滑

20. 标准差因子（Concerned）

因子构造

选定股票，逐个交易日回顾分钟单笔成交金额序列；
保留 10%单笔成交金额较小的样本计算标准差，记作 D 指标；
计算 D 指标的 20 日均值，即为 STD 因子

因子说明

从变量的离散程度观察单笔成交金额分布。
数据：逐笔成交

参考文献

2022-06-12_开源证券_金融工程_市场微观结构研究系列（15）：高频因子：分钟单笔金额序列中的主力行为刻画

注意事项

不进行滚动20日平滑，也可构造1个因子

注释

保留成交金额较小者
同时构造了两个因子

21.高频偏度（Concerned）

因子构造

$$\text { 高频偏度 }=\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\sqrt{N} \sum_{j=1}^N r_{i, j, n}^3}{\left(\sum_{j=1}^N r_{i, j, n}^2\right)^{1.5}}$$

其中， i、 j、 n 分别代表第 i 只股票、第 j 分钟和第 n 个交易日。月度选股下 T 取 20，周度选股下 T 取 5

因子说明

高频偏度刻画了股票价格日内快速拉升或下跌的特征。假设有两只股票日内涨幅相同，其中一只股票的涨幅由持续稳定的小幅上涨累计而来，而另一只股票的上涨源自于短期的大幅拉升，那么后者在未来有较大概率出现收益反转。从风险溢价角度来看，日内经常快速下跌，或者下行风险大的股票具有更高的风险溢价。
数据：基于分钟成交数据的高频因子
选股效果较强

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想
Amaya et al. (2011) 《Does Realized Skewness and Kurtosis Predict the Cross-Section of Equity Returns?》

注释

未进行滚动平滑构造因子

22. 信息分布均匀度（Concerned）

因子构造

每月月底，回溯所有股票过去 20 个交易日，每个交易日都利用分钟数据，计算日内分钟涨跌幅的标准差，记为每日的高频波动率 Vol_daily；
每只股票，计算 20 个 Vol_daily 的标准差，记为该股票当月每日波动率的波动 std（ Vol_daily）；
每只股票，计算 20 个 Vol_daily 的平均值，衡量该股票当月每日波动率的平均水平 mean（ Vol_daily）；将 std（ Vol_daily）除以 mean（ Vol_daily），再做市值中性化处理，得到每只股票的信息分布均匀度 UID 因子，即$$\text { 信息分布均匀度 UID }=\frac{\text { 高频波动率的标准差 std(Vol_daily) }}{\text { 高频波动率的平均值 mean(Vol_daily) }}$$

因子说明

数据：分钟K线

参考文献

2020-09-01_东吴证券_“波动率选股因子”系列研究（二）：信息分布均匀度，基于高频波动率的选股因子

注释

计算的日频因子，没有进行平滑

23. 振幅因子（Look on）

因子构造

振幅因子=日度价格最高值/最低值-1

因子说明

振幅因子可对常见价量类因子进行有效补充
数据：每日量价数据

参考文献

2019-09-24_海通证券_选股因子系列研究（五十五）：价量波动幅度

注意事项

效果存疑

二. 相关性

1. 日内价量相关性 corr_VP（Concerned）

因子构造

$$𝑐𝑜𝑟𝑟_𝑉𝑃_{𝐷,𝑖}=𝑐𝑜𝑟𝑟(𝑣_{𝑡,𝐷,𝑖}, 𝑝_{𝑡,𝐷,𝑖})$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的价格序列为${p_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇

因子说明

价量相关性是指价格序列和成交量序列的相关性
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

2. 收益率与量相关性 corr_VR（Concerned）

因子构造

$$corr_VR_{D,i}=corr(v_{t,D,i}, r_{t,D,i})$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的收益率序列为${r_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇

因子说明

收益率与成交量的相关性
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

3. 量与滞后收益率相关性 corr_VRlag（Concerned）

因子构造

$$corr_VRlag_{D,i}=corr(v_{t,D,i}, r_{t-1,D,i})$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的收益率序列为${r_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇

因子说明

滞后收益率与成交量的相关性
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

4. 量与超前收益率相关性 corr_VRlead（Concerned）

因子构造

$$corr_VRlead_{D,i}=corr(v_{t,D,i}, r_{t+1,D,i})$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的收益率序列为${r_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇

因子说明

超前收益率与成交量的相关性

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

5. Amihud非流动性因子 Amihud_illiq（Good）

因子构造

$$\text { Amihud_illiq }{D, i}=\frac{1}{T-1} \sum{t=2}^T \frac{\left|r_{t, D, i}\right|}{p_{t, D, i} v_{t, D, i}}$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的收益率序列为${r_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的价格序列为${p_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇

因子说明

考虑单位成交额驱动下，股价的变化幅度。
因子值越大，说明股票的价格越容易被交易行为所影响（即流动性越低）。
通常是日频，可以缩短时间间隔到分钟
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

注意量纲，避免数据精度不足

注释

结果乘了10000

6. 开盘后半小时corr_VP corr_VPH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

7. 开盘后半小时corr_VR corr_VRH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

8. 开盘后半小时corr_Vrlead corr_VrLeadH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

9. 开盘后半小时corr_VrLag corr_VrLagH1（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

10. 收盘前半小时corr_VP corr_VPH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

14:57之后数据是否包含

11. 收盘前半小时corr_VR corr_VRH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

14:57之后数据是否包含

注释

包含

12. 收盘前半小时corr_Vrlead corr_VrLeadH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

14:57之后数据是否包含

注释

包含

13. 收盘前半小时corr_VrLag corr_VrLagH8（Concerned）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

14:57之后数据是否包含

注释

包含

14. 大成交量价量相关性 corr_VPlarge（Concerned）

因子构造

$$𝑐𝑜𝑟𝑟_𝑉𝑃_{𝐷,𝑖}=𝑐𝑜𝑟𝑟(𝑣_{𝑡,𝐷,𝑖}, 𝑝_{𝑡,𝐷,𝑖})$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的价格序列为${p_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
将个股在每个交易日的分钟成交量时间序列按照成交量大小排序，将分钟成交量排名前1/3的成交量定义为“大成交量”。

因子说明

在不同的成交中，大单成交与主力资金关联较大，蕴含的信息可能更多。
针对大成交量对应的时刻的股价信息，可以构建大成交量相关因子

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

15. 大成交量量与滞后收益率相关性 corr_VRlaglarge（Concerned）

因子构造

$$corr_VRlag_{D,i}=corr(v_{t,D,i}, r_{t-1,D,i})$$

股票日内分钟频率下的成交量序列为${𝑣_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
股票日内分钟频率下的收益率序列为${r_{𝑡,𝐷,𝑖}}$, 𝑡 = 1,2,3, ⋯ , 𝑇
将个股在每个交易日的分钟成交量时间序列按照成交量大小排序，将分钟成交量排名前1/3的成交量定义为“大成交量”。

因子说明

在不同的成交中，大单成交与主力资金关联较大，蕴含的信息可能更多。
针对大成交量对应的时刻的股价信息，可以构建大成交量相关因子

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

16. 主力交易强度因子 MTS（Good）

因子构造

选定股票，逐个交易日回顾分钟单笔成交金额和分钟成交额
计算单笔成交金额与成交额的相关系数，记为 TS 指标
滚动 20 个交易日计算 TS 指标的均值，即 MTS 因子

因子说明

单笔成交金额与成交额之间的相关性强弱，描述的是代表主力的“相对大单” 对分钟成交额的影响。
从资金行为学的角度来理解，单笔成交金额与成交额的相关性越强，主力资金主导成交节奏的能力也越强。
数据：分钟成交额，分钟成交笔数

参考文献

2022-06-12_开源证券_金融工程_市场微观结构研究系列（15）：高频因子：分钟单笔金额序列中的主力行为刻画

注意事项

单笔成交金额，使用分钟内单笔成交额均值代替？

注释

同时计算了滚动和单日因子

17. 主力交易情绪因子 MTE（Concerned）

因子构造

选定股票，逐个交易日回顾分钟单笔成交金额和分钟收盘价；
计算单笔成交金额与收盘价的相关系数，记为 TE 指标
滚动 20 个交易日计算 TE 指标的均值，即 MTE 因子

因子说明

MTE 因子实质上反映了主力参与交易的相对价位，因子值越大，表明主力交易更倾向于出现在高价位，这是“逢高出货”的表现，反映了主力悲观态度；而因子值越小，则表明主力交易更多出现在低价位，这是“逢低吸筹”的表现，属于乐观情绪。
这个理解框架与我们交易行为因子中的“聪明钱因子”比较相似
数据：分钟K线数据

参考文献

2022-06-12_开源证券_金融工程_市场微观结构研究系列（15）：高频因子：分钟单笔金额序列中的主力行为刻画

注意事项

单笔成交金额，使用分钟内单笔成交额均值代替？

注释

同时计算了滚动和单日因子

三. 收益率

1. 日内收益率 ret_intraday（Look on）

因子构造

$$ret_intraday_{D,i}=\frac{p_{T,D,i}}{open_{D,i}}-1$$

分子为股票当日收盘价
分母为股票当日开盘价

因子说明

根据日内股价的形态构造的价格形态衍生因子，只考虑日内的股价变化。
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

效果存疑

2. 日内最大回撤 intraday_maxdrawdown（Good）

因子构造

$$\text { intraday_maxdrawdown }_{D, i}=\min {0<t<T} \min {0<\tau \leq T-t} \frac{p{t+\tau, D, i}}{p{t, D, i}}-1$$

因子说明

日内最大回撤表示分钟行情价格的最大回撤，取值范围为(−1,0]

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

剔除没有成交额的分钟时段

注释

采用了（波谷-波峰）/波峰的简便算法。

3. 开盘后半小时收益率 ret_H1（Look on）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

效果存疑

4. 开盘后半小时至收盘的收益率 ret_close2H1（Look on）

因子构造

按照名字构造即可

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

效果存疑

5. 开盘价相对第一阶段集合竞价最高价的收益率 ret_open2AH1（Good）

因子构造

按照名字构造即可

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

由于没有集合竞价的分钟high数据，选择ask_price替代

6. 开盘价相对第一阶段集合竞价最低价的收益率 ret_open2AL1（Concerned）

因子构造

按照名字构造即可

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

由于没有集合竞价的分钟high数据，选择bid_price替代。

7. 开盘价相对第二阶段集合竞价最低价的收益率 ret_open2AL2（Good）

因子构造

按照名字构造即可

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

由于没有集合竞价的分钟high数据，选择ask_price

8. 开盘价相对第二阶段集合竞价最高价的收益率 ret_open2AH2（Concerned）

因子构造

按照名字构造即可

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注释

由于没有集合竞价的分钟high数据，选择采用ask_price

9. 隔夜收益率 ret_overnight（Concerned）

因子构造

开盘价相对前一交易日收盘价的收益率

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

10. 尾盘半小时收益率 ret_H8（Concerned）

因子构造

收盘前半小时的收益率

因子说明

特定时段采样
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

注意事项

是否剔除14:57后数据

注释

未剔除

四. 占比

1. 趋势占比 trendratio（Concerned）

因子构造

$$\text { trendratio }{D, i}=\frac{p{T, D, i}-p_{1, D, i}}{\sum_{t=2}^T\left|p_{t, D, i}-p_{t-1, D, i}\right|}$$

因子说明

趋势占比可以衡量日内股价的趋势强度，取值范围为[−1,1]
日内价格变化/分钟频价格变化绝对值之和

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

2. 早盘半小时成交量占比 ratio_volumeH1（Concerned）

因子构造

$$ratio_volumeH1=\frac{trading_volume_in_first_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第1段成交量占全天成交量只比

因子说明

早盘成交量占比：开盘后第 1 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

3. 成交量占比H2 ratio_volumeH2（Concerned）

因子构造

$$ratio_volumeH2=\frac{trading_volume_in_second_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第2段成交量占全天成交量只比

因子说明

开盘后第 2 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

4. 成交量占比H3 ratio_volumeH3（Concerned）

因子构造

$$ratio_volumeH3=\frac{trading_volume_in_thrid_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第3段成交量占全天成交量只比

因子说明

开盘后第 3 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

5. 成交量占比H4 ratio_volumeH4（Concerned）

因子构造

$$ratio_volumeH4=\frac{trading_volume_in_fourth_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第4段成交量占全天成交量只比

因子说明

开盘后第 4 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

6. 成交量占比H5 ratio_volumeH5（Concerned）

因子构造

$$ratio_volumeH5=\frac{trading_volume_in_fifth_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第5段成交量占全天成交量只比

因子说明

开盘后第 5 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

7. 成交量占比H6 ratio_volumeH6（Concerned）

因子构造

$$ratio_volumeH6=\frac{trading_volume_in_sixth_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第6段成交量占全天成交量只比

因子说明

开盘后第 6 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

8. 成交量占比H7 ratio_volumeH7（Concerned）

因子构造

$$ratio_volumeH7=\frac{trading_volume_in_seventh_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第7段成交量占全天成交量只比

因子说明

开盘后第 7 个半小时成交量占全天成交量之比

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

9. 尾盘半小时成交量占比 ratio_volumeH8（Concerned）

因子构造

$$ratio_volumeH8=\frac{trading_volume_in_last_30min}{total_trading_volume}$$

对于4个小时的股票交易时间，平均分成8段，第8段成交量占全天成交量只比

因子说明

尾盘成交量占比：开盘后第 8 个半小时成交量占全天成交量之比
效果较好

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

10. 尾盘成交额占比 𝑇𝑇𝑉_𝑅𝑎𝑡𝑖𝑜_𝐷（Concerned）

因子构造

$$TTV_Ratio_D_{i, T}=-\frac{\sum_{t=210}^{t=240} t t v_{i, t, T}}{F l o a t M V_T}$$

$ttv_{i,t,T}$为个股在 T 日第 t 分钟的成交额， $FloatMV_T$ 为 T 日的流通市值。

因子说明

量价数据，分钟K线数据

参考文献

2023-02-12_信达证券_信达金工指数增强系列报告之三：基于基金持仓、特色基本面因子以及高频价量因子的1000指数增强

注释

本因子是成交额，ratio_volumeH8是成交量

11. 连续竞价成交占比（Good）

因子构造

连续竞价成交金额/当日成交金额

因子说明

level2行情数据

参考文献

海通证券-20160606-选股因子系列研究（十一）： Level2行情选股因子初探

注释

连续竞价成交金额数据未知

12. 高低价格区间成交笔数占比因子（Good）

因子构造

$$\text{高低价格区间成交笔数占比}=\frac{\sum_{j=1}^N \text { matchitems } * I_{j \in \text {set_a}}}{\sum_{j=1}^N matchitems}$$

$𝐼_{𝑗 ∈ 𝑠𝑒𝑡_𝑎}$表示快照所属区间的判断，其中，$set_a$ 代表处于高低价格区间的快照集合，例如将 20%作为价格区间判定标准，则计算高价格区间相关因子时， set_a 即为按照价格排序的前 20%快照的集合。

因子说明

高低价格区间成交笔数占比因子是价格区间内所有快照的成交笔数累加与全天成交总笔数的比值
高低价格区间成交笔数占比因子能够反映价格区间内成交聚集程度。
数据：3s快照

参考文献

2021-10-15_东兴证券_另辟蹊径系列之一：基于高频快照数据的行为追踪因子

13. 高低价格区间成交量占比因子（Concerned）

因子构造

$$\text{高低价格区间成交量占比}=\frac{\sum_{j=1}^N \text { volumes } * I_{j \in \text {set_a}}}{\sum_{j=1}^N volumes}$$

$𝐼_{𝑗 ∈ 𝑠𝑒𝑡_𝑎}$表示快照所属区间的判断，其中，$set_a$ 代表处于高低价格区间的快照集合，例如将 20%作为价格区间判定标准，则计算高价格区间相关因子时， set_a 即为按照价格排序的前 20%快照的集合。

因子说明

高低价格区间成交量占比因子能够体现价格区间内交易资金量大小，直观体现交易的活跃程度。
股票日内快照数据中的成交量与成交笔数的相关性很高，但又包含不同的信息，成交量直观地体现了当前参与交易的资金量，成交笔数一定程度上反映了参与交易的投资者数量、下单的模式以及买卖方撮合的情况。
数据：3s快照

参考文献

2021-10-15_东兴证券_另辟蹊径系列之一：基于高频快照数据的行为追踪因子

14. 平均单笔流出金额占比（Concerned）

因子构造

$$\text { 平均单笔流出金额占比 }=\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\sum_{j=1}^N A m t_{i, j, n} \cdot I_{r_{i, j, n}<0} / \sum_{j=1}^N \operatorname{TrdNum_{i,j,n}\cdot I_{r_{i,j,n}<0}}}{\sum_{j=1}^N A m t_{i, j, n} / \sum_{j=1}^N \operatorname{TrdNum_{i,j,n}}}$$

其中， i、 j、 n 分别代表第 i 只股票、第 j 分钟和第 n 个交易日。月度选股下 T 取 20，周度选股下 T 取 5

因子说明

股票下跌时，如果单笔成交金额大，说明委买有大单，是一种抄底行为。
数据：基于分钟成交数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

15. 开盘后净委买增额占比（Good）

因子构造

$$开盘后净委买增额占比 =\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\sum_{j \in 9: 30-10: 00} \text { 净委买增额 }{ }{i, j, n}}{\text { 成交额 }{i, ; n}}$$

$净委买增额 _{i, j, n}= 委托买单增加量 _{i, j, n}- 委托卖单增加量 _{i, j, n}$
其中， i、 j、 n 分别代表第 i 只股票、第 j 分钟和第 n 个交易日。月度选股下 T 取 20，周度选股下 T 取 5

因子说明

盘口委托挂单数据刻画了投资者的买入意愿，开盘后 30 分钟内的委买增量越大，投资者在这段时间内的买入意愿越强。
数据：基于tick委托数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

注释

乘了100.

16. 开盘后净主买占比（Concerned）

因子构造

$$\text { 开盘后净主买占比 }=\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\sum_{j \in 9: 30-10: 00} \text { 净主买成交额 }{ }{i, j, n}}{\sum{j \in 9: 30-10: 00} \text { 成交额 }{ }_{i, j, n}}$$

$\text { 净主买成交额 }{i, j, n} =\text { 主动买入成交额 }{i, j, n}-\text { 主动卖出成交额 }_{i, j, n}$

其中， i、 j、 n 分别代表第 i 只股票、第 j 分钟和第 n 个交易日。月度选股下 T 取 20，周度选股下 T 取 5

因子说明

逐笔成交数据中包含投资者主动买入和主动卖出的信息，将两者的成交金额相减即可得到净主动买入的金额（简称“净主买”）。开盘后净主买占比因子刻画了投资者在开盘后 30 分钟内，净买入行为的强度。开盘后净主买占比越高，投资者的主动买入行为越强。
数据：基于tick委托数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

17. 大买成交占比（Concerned）

因子构造

$$\text { 大买成交占比 }=\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\text { 大买单成交额 }{ }{i, ; n}}{\text { 成交额 }{i, ; n}}$$

在界定大小单时，可从单的成交量分布出发。例如，某一单的成交量处于当日成交量分布的均值+1 倍标准差之外，则可被认为是大单。
其中， i、 j、 n 分别代表第 i 只股票、第 j 分钟和第 n 个交易日。月度选股下 T 取 20，周度选股下 T 取 5

因子说明

基于逐笔成交数据中的单号，可将逐笔数据合成为单成交数据，并从单的角度区分大小单。再根据对应的“买”、“卖”标记，可进一步计算大买单占全天成交金额的比例（简称“大买成交占比”）。大买成交占比越高，大单买入行为越强。
数据：基于tick委托数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

注释

乘了10000

18. 开盘后净主买占比（Concerned）

因子构造

$$\text { 开盘后知情主卖占比 }=\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\sum_{j \in 9: 30-10: 00} \text { 知情主卖成交额 }{i, j, n}}{\sum{j \in 9: 30-10: 00} \text { 成交额 }_{i, j, n}}$$

首先需要下列回归：
$$r_{i, j, n}=\gamma_0+\sum_{k=1}^4 \gamma_{1, k} D_{k, i, j, n}^{\text {weekday }}+\sum_{k=1}^3 \gamma_{2, k} D_{k, i, j, n}^{\text {period }}+\gamma_3 r_{i, j-1, n}+\varepsilon_{i, j, n}$$
其中， $r_{i,j,n}$ 为股票 i 在 n 日第 j 分钟的收益； $D_{k,i,j,n}^{weekday}$ 为虚拟变量（ k=1, 2, 3, 4），分别表示周一至周四； $D_{k,i,j,n}^{period}$ 为时间段虚拟变量（ k=1, 2, 3），分别表示开盘后 30 分钟、盘中及收盘前 30 分钟； $r_{i,j-1,n}$ 为分钟收益滞后项。
残差序列为股票的预期外收益。当预期外收益为正时，投资者的主动卖出行为可被认为是知情主卖；反之，则被认为是知情主买。

因子说明

结合逐笔成交数据中的主买、主卖和预期外收益，可定义知情主卖，用以刻画知情交易者的卖出行为。开盘后知情主卖占比越高，知情交易者卖出行为越强，投资者对股票未来的表现越悲观。
数据：基于tick委托数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

注意事项

该方法的可实现程度，算力开销较大

19. 开盘后买入意愿占比（Concerned）

因子构造

$$开盘后买入意愿占比 =\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\sum_{j \in 9: 30-10: 00} \text { 买入意愿 }{i, j, n}}{\sum{j \in 9: 30-10: 00} \text { 成交额 }_{i, j, n}}$$

$买入意愿 _{i, j, n}= 净主买成交额 {i, j, n}+ 净委买增额 { }{i, j, n}$

因子说明

委托挂单体现投资者尚未释放的交易意愿，而主买/主卖则代表已进行的交易行为。若将两者结合，可以得到广义的投资者主动买入意愿。开盘后 30 分钟内买入意愿占比越高，投资者的买入意愿越强。
数据：TICK 委托与逐笔成交数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

注意事项

委买数据的量级

20. 主买占比因子（Concerned）

因子构造

主买占比（占全天成交额）：主动买入金额/当日成交总金额
主买占比（占同时段成交额）：主动买入金额/同时段总成交金额

因子说明

结合逐笔成交数据中的主买、主卖和预期外收益，可定义知情主卖，用以刻画知情交易者的卖出行为。开盘后知情主卖占比越高，知情交易者卖出行为越强，投资者对股票未来的表现越悲观。
数据：日内分钟收益序列，基于tick的委托数据

参考文献

海通证券-20200214-选股因子系列研究（五十八) ：知情交易与主买主卖

注释

计算了全天

21. volumeinflowrate_open（Concerned）

因子说明

开盘资金流入率, 10点前的资金净流入量/10点前的成交股数

wind提供的资金流向因子

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

注意事项

资金净流入量的定义

注释

（主买-主卖）作为资金净流入量的定义

22. volumeinflowrate_close（Concerned）

因子说明

尾盘资金流入率, 14:30后的资金净流入量/14:30后的成交股数

wind提供的资金流向因子

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

注意事项

资金净流入量的定义

注释

（主买-主卖）作为资金净流入量的定义

23. amountinflow_rate（Concerned）

因子说明

净流入率，当日净流入/成交额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

注意事项

资金净流入量的定义

注释

（主买-主卖）作为资金净流入量的定义

24. 平均单比流出金额占比（Concerned）

因子构造

$$平均单比流出金额占比=\frac{\sum_{i=1}^NAmt_iI_{r_i<0}/\sum_{i=1}^NTrdNum_iI_{r_i<0}}{\sum_{i=1}^NAmt_i/\sum_{i=1}^NTrdNum_i}$$

其中， $Amt_i$ 代表第 i 根 K 线成交额， $TrdNum_i$ 代表第 i 根 K 线成交笔数，而$I_{r_i}<0$ 则代表第 i 根 K 线是否下跌。该因子希望可以刻画下跌时段的多空强度相对于全天所有时段的比例情况。

因子说明

数据：分钟K线

参考文献

海通证券-20200622-选股因子系列研究（六十六）：寻找逐笔交易中的有效信息

注释

与14因子一样，这个是当天，那个是平滑。只选择了一个构造，只构造了当天的。

25. 大单资金净流入率（Concerned）

因子构造

$$大单资金净流入率=(\sum_{i=1}^NAmt_iI_{r_i>0,i\in IdxSet}-\sum_{i=1}^NAmt_iI_{r_i<0,i\in IdxSet})/\sum_{i=1}^NAmt_i$$

其中， $Amt_i$ 代表第 i 根 K 线成交额， $I_{r_i}<0$ 则代表第 i 根 K 线是否下跌。定义了大单 K 线的概念，即$I_{i\in IdxSet}$ 表示该 K 线是否为全天所有K 线当中，平均每笔成交额最大的前 10%的 K 线

因子说明

数据：分钟K线

参考文献

海通证券-20200622-选股因子系列研究（六十六）：寻找逐笔交易中的有效信息

26. 大卖成交金额占比（Concerned）

因子构造

$$大卖成交金额占比_{i,t}=\frac{大卖成交金额_{i,t}}{总成交金额_{i,t}}$$

因子说明

数据：逐笔成交
由于一个买单或者卖单会因对手盘的挂单结构而被切分为多笔成交，因此在刻画投资者行为时，可将逐笔成交数据还原为买卖单数据，并从买卖单的角度进行分析
- 通过叫卖序号判断是否为同一订单
使用了“N 倍标准差” 的方式，在每个交易日对于每个股票单独设定大单筛选阈值。每个交易日，各股票的大单筛选流程如下：
- 基于股票买卖单成交量，计算成交量标准差
- 将成交量大于均值+N 倍标准差的买卖单认定为大单

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

27. 大买成交金额占比（Concerned）

因子构造

$$大买成交金额占比_{i,t}=\frac{大买成交金额_{i,t}}{总成交金额_{i,t}}$$

因子说明

数据：逐笔成交
由于一个买单或者卖单会因对手盘的挂单结构而被切分为多笔成交，因此在刻画投资者行为时，可将逐笔成交数据还原为买卖单数据，并从买卖单的角度进行分析
- 通过叫卖序号判断是否为同一订单
使用了“N 倍标准差” 的方式，在每个交易日对于每个股票单独设定大单筛选阈值。每个交易日，各股票的大单筛选流程如下：
- 基于股票买卖单成交量，计算成交量标准差
- 将成交量大于均值+N 倍标准差的买卖单认定为大单

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

28. 大买+大卖成交占比因子（Concerned）

因子构造

参与成交买卖订单双方成交额均超过全天所有订单成交额均值的成交金额占比。

因子说明

数据：逐笔成交

参考文献

海通证券-20201218-选股因子系列研究（七十一）：逐笔大单因子与大资金行为

29. 大单因子（Concerned）

因子构造

参与成交买卖订单有一方成交额超过全天所有订单成交额均值的成交金额占比。

因子说明

数据：逐笔成交

参考文献

海通证券-20201218-选股因子系列研究（七十一）：逐笔大单因子与大资金行为

30. 剔除大买的大卖因子（Good）

因子构造

参与成交买卖订单中，卖单成交额均超过全天所有订单成交额均值，而买单成交金额没有超过全天所有订单成交金额均值的成交金额占比。

因子说明

数据：逐笔成交

参考文献

海通证券-20201218-选股因子系列研究（七十一）：逐笔大单因子与大资金行为

31. 大买因子（Concerned）

因子构造

参与成交买卖订单中，买单成交额均超过全天所有订单成交额均值的成交金额占比

因子说明

数据：逐笔成交

参考文献

海通证券-20201218-选股因子系列研究（七十一）：逐笔大单因子与大资金行为

五. 盘口

1. 第一阶段集合竞价振幅 diverge_A1

因子构造

按照名字构造

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

2. 第二阶段集合竞价振幅 diverge_A2

因子构造

按照名字构造

因子说明

盘前信息，主要包括隔夜收益率（开盘价相对前收盘的收益率）和开盘前集合竞价信息
A股证券交易所在每个交易日的9:15至9:25为开盘集合竞价时间。开盘集合竞价又分为两个阶段
- 第一阶段是9:15至9:20，该阶段允许撤销已经提交的订单；
- 第二阶段是9:20至9:25，该阶段目前不允许撤销已经提交的订单。

参考文献

广发证券-金融工程-20230312-多因子 alpha 系列报告之（四十八）：高频数据的因子化研究

3. 买卖压力

因子构造

$$P=log(Pbuy)-log(Psell)$$

其中，$$\begin{aligned}& \text { Pbuy }=\sum \operatorname{Vol}_i\left[\text { Close } /\left(P_i-\text { Close }\right)\right] / \sum \text { Close } /\left(P_i-\text { Close }\right) \& \text { Psell }=\sum \operatorname{Vol}_i\left[\text { Close } /\left(P_i-\text { Close }\right)\right] / \sum \text { Close } /\left(P_i-\text { Close }\right)\end{aligned}$$
close为当日收盘价，$P_i$ 为挂单价格，$Vol_i$ 为挂单量

因子说明

数据：盘口数据

参考文献

天风证券-20170801-利用高频数据拓展盘口数据：买卖压力失衡

注释

首先对240个分钟数据计算P-close，剔除掉该项为0的数据。

4. 订单失衡 Volume Order Imbalance, VOI1

因子构造

$$V O I 1_t=\Delta V_t^B-\Delta V_t^A$$

$$\Delta V_t^B=\left{\begin{array}{ll}0 & P_t^B<P_{t-1}^B \ V_t^B-V_{t-1}^B & P_t^B=P_{t-1}^B \ V_t^B & P_t^B>P_{t-1}^B\end{array} \quad, \quad \Delta V_t^A= \begin{cases}V_t^A & P_t^A<P_{t-1}^A \ V_t^A-V_{t-1}^A & P_t^A=P_{t-1}^A \ 0 & P_t^A>P_{t-1}^A\end{cases}\right.$$
$𝑃_𝑡^𝐵$ 和$𝑃_𝑡^𝐴$ 分别为t时刻的买一价和卖一价，$𝑉_𝑡^𝐵$ 和$𝑉_𝑡^𝐴$ 分别是t时刻的买一和卖一的委托量。

因子说明

订单失衡是一个重用的信号，它使我们能够了解市场的总体情绪和方向。知情交易者鉴于正面（负面）消息或交易者根据市场情绪的好坏，他们将会决定持有多头（或空头）头寸，从而增加资产的不平衡。由于不同时刻知情交易者拥有信息的准确性程度不同和市场交易情绪不同，其订单不平衡程度也有所差异。如在限价订单簿中观察到此现象，市场参与者将能够使用此信息并制定策略以获得正向收益。
数据：盘口

参考文献

中信建投证券-20200709-高频量价选股因子初探：因子深度研究系列

5. 改进订单失衡 Volume Order Imbalance, VOI2

因子构造

$$V O I 2_t=\Delta V_t^{WB}-\Delta V_t^{WA}$$

$$V_t^{W B(W A)}=\frac{\sum w_i \times V_{i, t}^{B(A)}}{\sum w_i} \quad, \quad w=1-(\mathrm{i}-1) / 5, \quad \mathrm{i}=1,2,3,4,5$$
$$\Delta V_t^B=\left{\begin{array}{ll}0 & P_t^B<P_{t-1}^B \ V_t^B-V_{t-1}^B & P_t^B=P_{t-1}^B \ V_t^B & P_t^B>P_{t-1}^B\end{array} \quad, \quad \Delta V_t^A= \begin{cases}V_t^A & P_t^A<P_{t-1}^A \ V_t^A-V_{t-1}^A & P_t^A=P_{t-1}^A \ 0 & P_t^A>P_{t-1}^A\end{cases}\right.$$
$𝑃_𝑡^𝐵$ 和$𝑃_𝑡^𝐴$ 分别为t时刻的买一价和卖一价，$𝑉_𝑡^𝐵$ 和$𝑉_𝑡^𝐴$ 分别是t时刻的买一和卖一的委托量。

因子说明

传统VOI计算只考虑了第一档的盘口数据，这将遗漏掉很多有价值的信息，为充分利用盘口数据信息，利用衰减加权的方法对委托量加权，得到加权后的委托量$𝑉_𝑡^{𝑊𝐵}$ 、$𝑉_𝑡^{𝑊𝐴}$ ,i表示挡位。
数据：盘口

参考文献

中信建投证券-20200709-高频量价选股因子初探：因子深度研究系列

6. 订单失衡率 Order Imbalance Ratio, OIR

因子构造

$$\mathrm{OIR}_t=\frac{V_t^{W B}-V_t^{W A}}{V_t^{W B}+V_t^{W A}}$$

$$V_t^{W B(W A)}=\frac{\sum w_i \times V_{i, t}^{B(A)}}{\sum w_i} \quad, \quad w=1-(\mathrm{i}-1) / 5, \quad \mathrm{i}=1,2,3,4,5$$

因子说明

OIR是另外一个衡量订单不平衡性质的变量，因此它的统计性质和VOI因子相似。我们充分利用盘口各档数据信息，以期得到更加准确的订单失衡比率OIR。不同挡位的盘口数据包含了不同层次的数据信息，此处仍采用衰减加权的方法对委托量加权，根据对买卖压力的影响力的不同将不同挡位赋予相应权重，给高挡位赋予更高的权重比例。
OIR为买卖委托量差与其和的比值，衡量了不均衡程度在其总买卖委托量中的占比。OIR为正说明市场买压大于卖压，未来价格趋向上涨，且OIR的比值越大，其上涨的概率越高，反之亦然。
数据：盘口

参考文献

中信建投证券-20200709-高频量价选股因子初探：因子深度研究系列

7. 市价偏离度Mid-Price Basis, MPB

因子构造

$$M P B_t=\overline{T P}t-\frac{M_t+M{t-1}}{2}=\overline{T P}_t-\overline{M P_t}$$

$$M_t=\frac{P_t^B+P_t^A}{2}$$
$$\overline{T P}t= \begin{cases}\frac{T_t}{V_t} & V_t \neq 0\
\overline{T P{t-1}} & V_t=0\end{cases}$$

因子说明

首先我们计算平均交易价格$\overline{TP_t}$ 。当股票在分钟t没有产生任何交易，即$𝑉_𝑡$和$𝑇_𝑡$均为零，此时$\overline{TP_t}$考虑到这时间段没有任何交易产生，因此时刻t的平均交易价格应该和上一时刻的价格相同。当时刻t内有交易产生的时侯，我们计算得到的平均市场交易价格等于时刻t的市场成交额除以时刻t的市场成交总量。
然后计算市场中间价，$𝑀_𝑡$ 为买一价和卖一价的平均。$𝑀𝑃𝐵_𝑡$ 为平均市场交易价格与平均市场中间价的差
数据：盘口数据，逐笔成交

参考文献

中信建投证券-20200709-高频量价选股因子初探：因子深度研究系列

8. 逐档订单失衡率Step Order Imbalance Ratio, SOIR

因子构造

$$\operatorname{SOIR}{i, t}=\frac{V{i, t}^B-V_{i, t}{ }^A}{V_{i,t}^B+V_{i, t}{ }^A}$$

$$\operatorname{SOIR}t=\frac{\sum{i=1}^5 w_i SO I R^{i, t}}{\sum_{i=1}^5 w_i}$$
$$w=1-(\mathrm{i}-1) / 5, \quad \mathrm{i}=1,2,3,4,5$$

因子说明

$SOIR_i$ 衡量了买卖委托量不均衡程度在其总量中的占比
数据：盘口数据

参考文献

中信建投-20210129-因子深度研究系列：高频订单失衡及价差因子

9. Spread_date

因子构造

$$\text { Spread_Month }m=\frac{1}{\sum_t w_t} * \sum_t w_t * \text { Spree } \widehat{a d{-} D a t} e_t$$

其中
- $$\widehat{Spread_Date_t}=\frac{Spread_Date_t-Mean(Spread_Date_t)}{std(Spread_Date_t)}$$
- $$\text { Spread_Date }t=\frac{1}{2 N} * \sum_i \text { Spread_Tick }{t, i} * I_{\text {volume }_{t, i}<\text { Median_Volume }_t}$$
- $$Spread_Tick=\frac{BID-ASK}{BID+ASK}$$
其中$\widehat{𝑆𝑝𝑟𝑒𝑎𝑑_𝐷𝑎𝑡𝑒_𝑡}$ 为月份 m 第 t 个交易日的盘口 Spread； $w_t = 𝑡/𝑛, 𝑡 ≤ 𝑛$为各交易日指标值的权重， n 为月份 m 的交易日数。

因子说明

月度数据，日度数据在过程中
spread_tick: 指标值越大意味着当前买盘挂单强度越大，股价短期上涨的概率越大；指标值越小则意味着当前盘口卖压越大，价格短期下行的概率越大。
spread_date: 为在低频多因子模型中引入盘口信息，我们需要将对 Spread 指标进行降频处理。为分析指标在低频结构下的特征，我们对每只股票的每日盘口相对强弱 Spread 取平均值以得到当日的整体的盘口买卖相对强弱度量值。

参考文献

天风证券-20190905-市场微观结构探析系列之二：订单簿上的alpha

注释

只构造到日频因子。

六. 知情交易

1. 交易量变异系数 Volume Coefficient of Variation, VCV

因子构造

$$VCV_{i,t} \equiv \frac{\sigma_{V(i,t)}}{\mu_{V(i,t)}}$$

月度公司级观测值是用日交易量的月标准差除以日交易量的月平均值来计算的。

因子说明

用这个因子来刻画知情交易者存在的可能性大小。
交易量可以用其他变量，比如成交额、个股日成交量在全市场成交量中的占比等替换。报告中使用成交额计算。

参考文献

招商证券-投资策略-20230513-高频寻踪：再觅知情交易者的踪迹：vcv因子的构建与解析

2. 指令流毒性 VPIN

因子构造

$$V P I N=\frac{\alpha \mu}{\alpha \mu+2 \varepsilon} \approx \frac{1}{N} \sum_{\tau=1}^N\left|V_\tau^S-V_\tau^B\right| / V$$

其中，$$\begin{gathered}V_\tau^B=\sum_{i=t(\tau-1)+1}^{t(\tau)} V_i Z\left(\frac{P_i^E-P_i^B}{\sigma_{\Delta P}}\right) \V_\tau^S=\sum_{i=t(\tau-1)+1}^{t(\tau)} V_i\left[1-Z\left(\frac{P_i^E-P_i^B}{\sigma_{\Delta P}}\right)\right]=V-V_\tau^B\end{gathered}$$
将𝑉设定为样本期内日均成交量的五十分之一，单位为股（按单边交易计算），同时取𝑁 = 50
$𝑉^𝐵_𝜏$（买方驱动成交量）和 $𝑉_𝜏^𝑆$（卖方驱动成交量）需要在单个交易量篮子中计算，因而我们要先根据日均成交量的五十分之一来划分交易篮子

因子说明

指令流毒性”（VPIN）指的是市场上知情交易者存在的可能性
VPIN是PIN的近似计算，但是在形式上简单得多，克服了在交易量很大的市场里估计 PIN 的困难，具备实际操作性， VPIN模型得到广泛使用，用于对市场流动性风险进行预测和预警

参考文献

2021-01-08_招商证券_“高频寻踪”系列之二：轻装上阵，高频数据因子的应用

3. 知情主买占比因子

因子构造

知情主买占比（占全天成交额）：知情主买额/当日成交额
知情主买占比（占同时段成交额）：知情主买额/当日同时段成交额
知情主买占比（占同时段主买）：知情主买额/当日同时段主买额
知情净主买占比（占全天成交额）：知情净主买额/当日成交额
知情净主买占比（占同时段成交额）：知情净主买额/当日同时段成交额
知情净主买占比（占同时段净主买）：知情净主买额/当日同时段净主买额
首先需要下列回归：
$$r_{i, j, n}=\gamma_0+\sum_{k=1}^4 \gamma_{1, k} D_{k, i, j, n}^{\text {weekday }}+\sum_{k=1}^3 \gamma_{2, k} D_{k, i, j, n}^{\text {period }}+\gamma_3 r_{i, j-1, n}+\varepsilon_{i, j, n}$$
其中， $r_{i,j,n}$ 为股票 i 在 n 日第 j 分钟的收益； $D_{k,i,j,n}^{weekday}$ 为虚拟变量（ k=1, 2, 3, 4），分别表示周一至周四； $D_{k,i,j,n}^{period}$ 为时间段虚拟变量（ k=1, 2, 3），分别表示开盘后 30 分钟、盘中及收盘前 30 分钟； $r_{i,j-1,n}$ 为分钟收益滞后项。
残差序列为股票的预期外收益。当预期外收益为正时，投资者的主动卖出行为可被认为是知情主卖；反之，则被认为是知情主买。
$\text { 知情净主买成交额 }{i, j, n} =\text { 知情主买成交额 }{i, j, n}-\text { 知情主卖成交额 }_{i, j, n}$

因子说明

结合逐笔成交数据中的主买、主卖和预期外收益，可定义知情主卖，用以刻画知情交易者的卖出行为。开盘后知情主卖占比越高，知情交易者卖出行为越强，投资者对股票未来的表现越悲观。
数据：日内分钟收益序列，基于tick的委托数据

参考文献

海通证券-20200214-选股因子系列研究（五十八) ：知情交易与主买主卖

4. 知情主卖占比因子

因子构造

知情主卖占比（占全天成交额）：知情主卖额/当日成交额
知情主卖占比（占同时段成交额）：知情主卖额/当日同时段成交额
知情主卖占比（占同时段主卖）：知情主卖额/当日同时段主卖额
首先需要下列回归：
$$r_{i, j, n}=\gamma_0+\sum_{k=1}^4 \gamma_{1, k} D_{k, i, j, n}^{\text {weekday }}+\sum_{k=1}^3 \gamma_{2, k} D_{k, i, j, n}^{\text {period }}+\gamma_3 r_{i, j-1, n}+\varepsilon_{i, j, n}$$
其中， $r_{i,j,n}$ 为股票 i 在 n 日第 j 分钟的收益； $D_{k,i,j,n}^{weekday}$ 为虚拟变量（ k=1, 2, 3, 4），分别表示周一至周四； $D_{k,i,j,n}^{period}$ 为时间段虚拟变量（ k=1, 2, 3），分别表示开盘后 30 分钟、盘中及收盘前 30 分钟； $r_{i,j-1,n}$ 为分钟收益滞后项。
残差序列为股票的预期外收益。当预期外收益为正时，投资者的主动卖出行为可被认为是知情主卖；反之，则被认为是知情主买。
$\text { 知情净主买成交额 }{i, j, n} =\text { 知情主买成交额 }{i, j, n}-\text { 知情主卖成交额 }_{i, j, n}$

因子说明

结合逐笔成交数据中的主买、主卖和预期外收益，可定义知情主卖，用以刻画知情交易者的卖出行为。开盘后知情主卖占比越高，知情交易者卖出行为越强，投资者对股票未来的表现越悲观。
数据：日内分钟收益序列，基于tick的委托数据

参考文献

海通证券-20200214-选股因子系列研究（五十八) ：知情交易与主买主卖

七. 强度/和差

1. 高低价格区间平均每笔成交量因子

因子构造

$$\text { 高低价格区间平均每笔成交量因子 }=\frac{\sum_{j=1}^N \text { volume } * I_{\left{j \in s e t _a\right}} / \sum_{j=1}^N \text { matchitems } * I_{\left{j \in s e t _a\right}}}{\sum_{j=1}^N \text { volume } / \sum_{j=1}^N \text { matchitems }}$$

$𝐼_{𝑗 ∈ 𝑠𝑒𝑡_𝑎}$表示快照所属区间的判断，其中，$set_a$ 代表处于高低价格区间的快照集合，例如将 20%作为价格区间判定标准，则计算高价格区间相关因子时， set_a 即为按照价格排序的前 20%快照的集合。

因子说明

高低价格区间平均每笔成交量因子能够衡量大小资金在股票日内高低价格区间的活跃程度。若价格区间内平均每笔成交量相对全天水平较大，则说明在这个区间内大资金相对活跃
数据：3s快照

参考文献

2021-10-15_东兴证券_另辟蹊径系列之一：基于高频快照数据的行为追踪因子

注释

分别计算高低

2. 开盘后净主买强度

因子构造

$$\text { 开盘后净主买强度 }=\frac{1}{T} \sum_{n=t}^{t-T+1} \frac{\operatorname{mean}{j \in 9: 30-10: 00}\left(\text { 净主买成交额 }{ }{i, j, n}\right)}{\operatorname{std}{j \in 9: 30-10: 00}\left(\text { 净主买成交额 }{ }{i, j, n}\right)}$$

$\text { 净主买成交额 }{i, j, n} =\text { 主动买入成交额 }{i, j, n}-\text { 主动卖出成交额 }_{i, j, n}$

因子说明

开盘后净主买强度因子刻画了投资者在开盘后 30 分钟内，净买入行为的稳健性。开盘后净主买强度越高，投资者的主动买入行为越稳健。
数据：基于tick委托数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

3. 开盘后买入意愿强度

因子构造

$$\text { 开盘后买入意愿强度 }=\frac{1}{T} \sum_{n=t}^{n=t-T+1} \frac{\operatorname{mean}{j \in 9: 30-10: 00}\left(\text { 买入意愿 }{i, j, n}\right)}{\operatorname{std}{j \in 9: 30-10: 00}\left(\text { 买入意愿 }{i, j, n}\right)}$$

$买入意愿 _{i, j, n}= 净主买成交额 {i, j, n}+ 净委买增额 { }{i, j, n}$

因子说明

开盘后 30 分钟内的买入意愿强度越高，投资者的买入意愿越稳健。
数据：TICK 委托与逐笔成交数据

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

4. 买单集中度

因子构造

$$买单集中度_{i,t}=\frac{\sum_{k=1}^{N_{i,t}}买单成交金额^2_{i,t,k}}{总成交金额^2_{i,t}}$$

买单成交金额 i,t,k 为股票 i 在交易日 t 的第 k 个买单的成交金额，卖单成交金额 i,t,k为股票 i 在交易日 t 的第 k 个卖单的成交金额，总成交金额 i,t 为股票 i 在交易日 t 的总成交金额。

因子说明

数据：逐笔成交

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

5. 卖单集中度

因子构造

$$卖单集中度_{i,t}=\frac{\sum_{k=1}^{N_{i,t}}卖单成交金额^2_{i,t,k}}{总成交金额^2_{i,t}}$$

买单成交金额 i,t,k 为股票 i 在交易日 t 的第 k 个买单的成交金额，卖单成交金额 i,t,k为股票 i 在交易日 t 的第 k 个卖单的成交金额，总成交金额 i,t 为股票 i 在交易日 t 的总成交金额。

因子说明

数据：逐笔成交

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

6. 买卖单集中度之和

因子构造

$$买卖单集中度之和 { }{i, t}=\frac{\sum{k=1}^{N_{i, t}} \text { 买单成交金额 }{ }{i, t, k}{ }^2}{\text { 总成交金额 }{ }{i, t}{ }^2}+\frac{\sum_{k=1}^{N_{i, t}} \text { 卖单成交金额 }{ }{i, t, k}{ }^2}{\text { 总成交金额 }{ }{i, t}{ }^2}$$

买单成交金额 i,t,k 为股票 i 在交易日 t 的第 k 个买单的成交金额，卖单成交金额 i,t,k为股票 i 在交易日 t 的第 k 个卖单的成交金额，总成交金额 i,t 为股票 i 在交易日 t 的总成交金额。

因子说明

数据：逐笔成交

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

7. 买卖单集中度差值

因子构造

$$买卖单集中度之和 { }{i, t}=\frac{\sum{k=1}^{N_{i, t}} \text { 买单成交金额 }{ }{i, t, k}{ }^2}{\text { 总成交金额 }{ }{i, t}{ }^2}-\frac{\sum_{k=1}^{N_{i, t}} \text { 卖单成交金额 }{ }{i, t, k}{ }^2}{\text { 总成交金额 }{ }{i, t}{ }^2}$$

买单成交金额 i,t,k 为股票 i 在交易日 t 的第 k 个买单的成交金额，卖单成交金额 i,t,k为股票 i 在交易日 t 的第 k 个卖单的成交金额，总成交金额 i,t 为股票 i 在交易日 t 的总成交金额。

因子说明

数据：逐笔成交

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

8. 主买强度因子

因子构造

$$日内主买强度 = \frac{mean(主动买入金额)}{std(主动买入金额)}$$
$$日内净主买强度 = \frac{mean(主动买入金额-主动卖出金额)}{std(主动买入金额-主动卖出金额)}$$

因子说明

考虑到使用日内不同时段数据计算得到的高频因子可能存在选股能力的差别，在计算因子时分别使用了 9:30~~14:56（简称为全天）、 9:30~~9:59（简称为开盘后）、 10:00~~14:26（简称为盘中）以及 14:27~~14:56（简称为收盘前）的数据
计算因子时依旧使用高频因子低频化的处理方式，即，每日计算当日指标值，在调仓日计算窗口期内指标均值作为当期因子值。以计算月度因子为例，股票因子值为股票前 20 交易日的指标均值。

参考文献

海通证券-20200113-选股因子系列研究（五十七）：基于主动买入行为的选股因子

9. 大买大卖成交金额占比差值

因子构造

$$大买大卖成交金额占比差值_{i,t}=\frac{大买成交金额_{i,t}}{总成交金额_{i,t}}-\frac{大卖成交金额_{i,t}}{总成交金额_{i,t}}$$

因子说明

数据：逐笔成交
由于一个买单或者卖单会因对手盘的挂单结构而被切分为多笔成交，因此在刻画投资者行为时，可将逐笔成交数据还原为买卖单数据，并从买卖单的角度进行分析
- 通过叫卖序号判断是否为同一订单
使用了“N 倍标准差” 的方式，在每个交易日对于每个股票单独设定大单筛选阈值。每个交易日，各股票的大单筛选流程如下：
- 基于股票买卖单成交量，计算成交量标准差
- 将成交量大于均值+N 倍标准差的买卖单认定为大单

参考文献

海通证券-20191107-选股因子系列研究（五十六）：买卖单数据中的Alpha

八. 反转因子

1. 高频反转因子

因子构造

$$高频反转因子=\frac{\sum vol_i*ret_i}{\sum vol_i}$$

其中$𝑟𝑒𝑡_𝑖$ 为每个时间段的对数收益率，$𝑣𝑜𝑙_𝑖$ 为对应时间段的的成交量

因子说明

分钟K线（5分钟K线）

参考文献

长江证券-20210128-基础因子研究（十六）：高频因子（十），量价关系中的反转微观结构

2. 成交量筛选的局部反转因子

因子构造

$$成交量筛选的局部反转因子_j=\sum{ret_i|q_j(vol_i)<vol_i<q_{j+1}(vol_i)}$$

其中$𝑟𝑒𝑡_𝑖$ 为每个时间段的对数收益率，$𝑣𝑜𝑙_𝑖$ 为对应时间段的的成交量
$𝑞_𝑗()$ 为分位数函数，本文中按照成交量分为五组，则𝑗 = 0,1,2,3,4,5 时$𝑞_𝑗(𝑣𝑜𝑙_𝑖)$ 分别代表$𝑣𝑜𝑙_𝑖$ 序列的 0%、20%、40%、60%、80%、100%分位数。根据𝑗的取值不同，该因子筛选出成交量大小不同的时间段(如𝑗 = 0时筛选出过去 20 个交易日的所有 K 线中成交量排名 0%-20%的时间段)，进而计算这些时间段内对数收益率和，作为因子值.

因子说明

数据：分钟K线（5分钟K线）

参考文献

长江证券-20210128-基础因子研究（十六）：高频因子（十），量价关系中的反转微观结构

3. 收益率绝对值筛选的局部反转因子

因子构造

$$收益率绝对值筛选的局部反转因子_j=\sum{ret_i|q_j(|ret_j|)<|ret_j|<q_{j+1}(|ret_j|)}$$

其中$𝑟𝑒𝑡_𝑖$ 为每个时间段的对数收益率
$𝑞_𝑗()$ 为分位数函数，本文中按照成交量分为五组，则𝑗 = 0,1,2,3,4,5 时$𝑞_𝑗(𝑣𝑜𝑙_𝑖)$ 分别代表$𝑣𝑜𝑙_𝑖$ 序列的 0%、20%、40%、60%、80%、100%分位数。根据𝑗的取值不同，该因子筛选出成交量大小不同的时间段(如𝑗 = 0时筛选出过去 20 个交易日的所有 K 线中成交量排名 0%-20%的时间段)，进而计算这些时间段内对数收益率和，作为因子值.

因子说明

数据：分钟K线（5分钟K线）

参考文献

长江证券-20210128-基础因子研究（十六）：高频因子（十），量价关系中的反转微观结构

4. 每笔成交量筛选的局部反转因子

因子构造

$$每笔成交量筛选的局部反转因子_j=\sum{ret_i|q_j(pvol_i)<pvol_i<q_{j+1}(pvol_i)}$$

其中$𝑟𝑒𝑡_𝑖$ 为每个时间段的对数收益率, $pvol_i$ 为每个时间段每笔成交量
$𝑞_𝑗()$ 为分位数函数，本文中按照成交量分为五组，则𝑗 = 0,1,2,3,4,5 时$𝑞_𝑗(𝑣𝑜𝑙_𝑖)$ 分别代表$𝑣𝑜𝑙_𝑖$ 序列的 0%、20%、40%、60%、80%、100%分位数。根据𝑗的取值不同，该因子筛选出成交量大小不同的时间段(如𝑗 = 0时筛选出过去 20 个交易日的所有 K 线中成交量排名 0%-20%的时间段)，进而计算这些时间段内对数收益率和，作为因子值.

因子说明

数据：分钟K线（5分钟K线）

参考文献

长江证券-20210128-基础因子研究（十六）：高频因子（十），量价关系中的反转微观结构

5. 每笔成交量标准化加权反转因子

因子构造

$$每笔成交量标准化加权反转因子=\frac{\sum w_i \times \text { ret}_i}{\operatorname{std}\left(\text { pvol}_i\right) \times \operatorname{std}\left(\text { ret}_i\right)}=corr (pvol,ret)$$

其中$𝑟𝑒𝑡_𝑖$ 为每个时间段的对数收益率, $pvol_i$ 为每个时间段每笔成交量

因子说明

数据：分钟K线（5分钟K线）

参考文献

长江证券-20210128-基础因子研究（十六）：高频因子（十），量价关系中的反转微观结构

注释

和corr组中的因子构造相同

6. 改进反转

因子构造

$$\text { 改进反转 }=\prod_{n=t}^{t-T+1} \frac{\text { Close }{i, j, n}}{\text { Close }{i, 10: 00, n}}-1$$

其中， i、 j、 n 分别代表第 i 只股票、第 j 分钟和第 n 个交易日。月度选股下 T 取 20，周度选股下 T 取 5

因子说明

大多数公司选择在收盘后发布财务数据等重要信息，造成股票次日往往跳空开盘，并在随后一段时间大幅波动。近年来， A 股机构投资者占比提升，市场交易行为在慢慢向美国等发达市场靠拢。这种在美股财报季常见的开盘跳空现象属于市场对重要数据或信息的合理定价，而非投资者行为造成的错误定价。基于以上推断，可以尝试将隔夜和开盘后半小时的涨幅剔除，构建改进反转因子。
数据：基于分钟成交数据的高频因子

参考文献

2020-07-30_海通证券_选股因子系列研究（六十九）：高频因子的现实与幻想

7. 理想反转因子

因子构造

回溯 20 个交易日，计算个股每日的平均单笔成交金额与涨跌幅；
选取单笔成交金额较高的 10 日，将其涨跌幅加总，记作$𝑀_{ℎ𝑖𝑔ℎ}$；
选取单笔成交金额较低的 10 日，将其涨跌幅加总，记作$𝑀_{𝑙𝑜𝑤}$；
将$𝑀_{ℎ𝑖𝑔ℎ}$减去$𝑀_{𝑙𝑜𝑤}$即可得到理想反转因子

因子说明

理想反转因子将单笔成交金额作为反转的强度指标，通过分割的方法得到过去20 日涨跌幅中的动量与反转信息。
因子的核心逻辑在于：单笔成交金额高的涨跌幅贡献较强的反转效应，而单笔成交金额低的涨跌幅反转效应较弱，甚至表现出轻微的动量效应。
数据：日度个股交易数据（金额）

参考文献

2022-06-12_开源证券_金融工程_市场微观结构研究系列（15）：高频因子：分钟单笔金额序列中的主力行为刻画

注释

构造时采用分钟频数据，将240分钟分成20组，计算每组的平均单笔成交金额和涨跌幅
选取单笔成交金额较高的10组，将涨跌幅加总
选取单笔成交金额较低的10组，将涨跌幅加总
相减

8. 强反转因子 SR

因子构造

回溯过去 20 个交易日内每分钟的涨跌幅和单笔成交金额；
将全部分钟涨跌幅按照单笔成交金额由大到小排序；
选取单笔成交金额前𝜆比例的涨跌幅加总，即为 SR 因子；

因子说明

引入参数𝜆的目的在于确定强反转因子的最优切割比例。当𝜆 取值较低时，SR因子的多空对冲更稳定，随着参数𝜆逐渐增大，累计涨跌幅的信噪比逐渐减低，因子多空净值也出现较为明显的回撤。
当𝜆取 10%时因子多空表现最好，但是多头收益相对较低，而保留 30%的比例，因子的多空最大回撤又会增加。因而权衡来看， 20%的保留比例更适合用于构造大单的“强反转”因子。
数据：逐笔成交，分钟K线

参考文献

2022-06-12_开源证券_金融工程_市场微观结构研究系列（15）：高频因子：分钟单笔金额序列中的主力行为刻画

注释

使用分钟频数据，按日度构造（不回溯）
lambda参数在param中可调

九. 数量

1. amountbuy_exlarge

因子说明

机构买入金额，单笔成交额大于 100 万元

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

2. amountsell_exlarge

因子说明

机构卖出金额，单笔成交额大于100万元

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

3. amountbuy_large

因子说明

大户买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

4. amountsell_large

因子说明

大户卖出金额,单笔成交额20万元至100万元之间

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

5. amountbuy_med

因子说明

中户买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

6. amountsell_med

因子说明

中户卖出金额，单笔成交额 4 万元到 20 万元之间

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

7. amountbuy_small

因子说明

散户买入金额，单笔成交额小于 4 万元

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

8. amountsell_small

因子说明

散户卖出金额，单笔成交额小于 4 万元

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

9. amountdiff_small

因子说明

散户净买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

10. amountdiff_smallact

因子说明

散户净主动买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

11. amountdiff_med

因子说明

中户净买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

12. amountdiff_medact

因子说明

中户净主动买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

13. amountdiff_large

因子说明

大户净买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

14. amountdiff_largeact

因子说明

大户净主动买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

15. amountdiff_exlarge

因子说明

机构净买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

16. amountdiff_exlargeact

因子说明

机构净主动买入金额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

17. moneyflow_diff

因子说明

净流入金额,当日主动买入总额-当日主动卖出总额

参考文献

广发证券-20210307-深度学习研究报告之七：深度学习框架下高频数据因子挖掘

十. 其他

1. 斜率凸性因子

因子构造

将股票在某一个 Tick 时刻的限价订单簿进行提取处理。针对买卖双方，分别从第一档开始将委托量进行累加。即，对于第 K 档委托，其累计委托量为：$Q_k=\sum_{i=1}^nQ_i$
进一步提取出每档累计委托量和每档委托价，得到其对应散点图。以第一档和第十档所在位置进行计算，得到了买卖双方所对应的斜率。同时考虑到股票间横截面可比的问题，我们以委托量占比的方式作为分母进行计算，并将买方斜率取负号得到正值，得到买卖方斜率因子： $𝑆𝑙𝑜𝑝𝑒_𝑎$， $𝑆𝑙𝑜𝑝𝑒_𝑏$
买卖方斜率差异因子 $Slope_{ab} = Slope_a-Slope_b$
进一步的，进行高低档位的切割，以探究不同档位斜率的特征。分别得到买卖方的高低档斜率因子$𝑆𝑙𝑜𝑝𝑒_{𝑎𝑙}$，$𝑆𝑙𝑜𝑝𝑒_{𝑏𝑙}$， $𝑆𝑙𝑜𝑝𝑒_{𝑎ℎ}$， $𝑆𝑙𝑜𝑝𝑒_{𝑏ℎ}$。
定义耐心程度差异因子 $Slope_{abl}=\frac{Slope_{al}-Slope_{bl}}{Slope_{al}+Slope_{bl}}$ , $Slope_{abh}=\frac{Slope_{ah}-Slope_{bh}}{Slope_{ah}+Slope_{bh}}$
定义斜率凸性因子 $Slope_{convex}=\frac{1}{3}Slope_{abh}+\frac{2}{3}Slope_{abl}$

因子说明

数据：沪深交易所提供的高频快照数据订单簿数据为每隔三秒的前十档买卖委托单的下单记录
根据推测，买方斜率越大，股票的需求弹性越小，买方投资者对于股票的价格敏感程度较低，则股票应有更高的预期收益。对于卖方而言，斜率越小则股票的供给弹性越大，即减少相同的价格会有较大程度的委托量降低，表明卖方不愿轻易降价卖出，同样对应到股票更高的预期收益。为了衡量买卖双方的弹性差异，计算买卖方斜率差异因子$Slope_{ab}$
一般而言，将委托单价格挂在远离中间价的位置是投资者更有耐心的体现，心理状态的不同可能会导致不同的预测效果。我们推测，低档位斜率因子与上述的供需弹性逻辑相符，即买方低档斜率越大，投资者对于价格的敏感程度越小，股票预期收益越高。卖方低档斜率越大，弹性越小，预期收益越低。而高档位投资者往往耐心程度更强，且其更有可能拥有优势信息，会与低档位投资者产生相反的预测效果。如买方高档斜率越大，投资者对于更低的价格区间形成了较为一致的预期，股票的预期收益更低。反之，卖方高档斜率越大，投资者的心理预期价格较高，股票预期收益越高。义了买卖双方对应档位的斜率差异因子以衡量双方的耐心程度差异。

参考文献

2023-06-26_国金证券_金融工程_alpha掘金系列之六：弹性与投资者耐心——基于高频订单簿的斜率凸性因子

2. 深度学习高频因子 RNN+NN

参考文献

2022-04-07_海通证券_金融工程_选股因子系列研究（七十七）：改进深度学习高频因子的9个尝试

3. 异常交易量因子 ATV

因子构造

过去 20 日的日均交易量（短期交易量）和过去 240 日的日均交易量（长期交易量）的商

因子说明

数据：日度交易数据

参考文献

2023-05-30_招商证券_投资策略_量化研究2023年中期投资策略：“持续异常交易量”选股因子patv

4. 持续异常交易量因子 patv

因子构造

计算“日内异常交易量” 𝑨𝑻𝑽𝒅；
- 在经典定义中，异常交易量因子等于短期交易量和长期交易量之比。因此类似地，我们以每只股票的分钟交易量衡量“短期交易量”，用股票过去一段时间所有的分钟交易量的均值衡量“分钟交易量中枢”，并将两者做商计算得到股票的日内异常交易量𝐴𝑇𝑉𝑑；
计算𝑨𝑻𝑽𝒅在截面上的排名分位数𝒓𝒂𝒏𝒌_𝑨𝑻𝑽𝒅；
- 通过计算每只股票的日内异常交易量𝐴𝑇𝑉𝑑在全市场的排名百分位𝑟𝑎𝑛𝑘_𝐴𝑇𝑉𝑑，我们可以对股票某分钟的异常交易量在全市场的相对水平进行衡量；
计算“日内持续异常交易量” 𝑷𝑨𝑻𝑽𝒅；
- 每一天，我们对每只股票进行以下计算：将第二步中𝑟𝑎𝑛𝑘𝐴𝑇𝑉𝑑的均值除以标准差，再加上其峰度，作为股票“日内持续异常交易量” 𝑃𝐴𝑇𝑉𝑑的衡量，具体如下式所示：$𝑃𝐴𝑇𝑉𝑑 =𝑀𝑒𝑎𝑛(𝑟𝑎𝑛𝑘{𝐴𝑇𝑉𝑑})/𝑆𝑡𝑑(𝑟𝑎𝑛𝑘_{𝐴𝑇𝑉𝑑}) + 𝐾𝑢𝑟𝑡(𝑟𝑎𝑛𝑘_{𝐴𝑇𝑉𝑑})$

因子说明

这个构建方法的思路在于， 𝑟𝑎𝑛𝑘_𝐴𝑇𝑉𝑑的均值越高，股票日内的异常交易量相对更高； 𝑟𝑎𝑛𝑘_𝐴𝑇𝑉𝑑的标准差越小，则该股票日内异常交易量相对更稳定；最后，如上文所述，高峰态的数据分布往往更集中。因此，三方面因素综合得到的股票“日内持续异常交易量” 𝑃𝐴𝑇𝑉𝑑，其数值越高，代表股票的日内异常交易量的持续性越强。

参考文献

2023-05-30_招商证券_投资策略_量化研究2023年中期投资策略：“持续异常交易量”选股因子patv

5. 价格筛选的局部成交量因子

因子构造

$$价格筛选的局部成交量因子_j=\frac{\sum{vol_i|q_j(close_i)<close_i<q_{j+1}(close_i)}}{\sum vol_i}$$

其中，$𝑐𝑙𝑜𝑠𝑒_𝑖$ 为每个时间段的收盘价，为使得不同成交量级的个股具有可比性，因子按照因子总成交量进行去量纲处理。

因子说明

数据：分钟K线（5分钟K线）

参考文献

长江证券-20210128-基础因子研究（十六）：高频因子（十），量价关系中的反转微观结构

6. 大单推动涨幅

因子构造

$$大单推动涨幅=\prod (1+r_i*I_{i\in IdxSet})$$

定义了大单 K 线的概念，即$I_{i\in IdxSet}$ 表示该 K 线是否为全天所有K 线当中，平均每笔成交额最大的前 10%的 K 线

因子说明

数据：分钟K线

参考文献

海通证券-20200622-选股因子系列研究（六十六）：寻找逐笔交易中的有效信息

7. 正交大单的大买因子

因子构造

大买因子对大单因子进行线性回归的残差。

大买因子：参与成交买卖订单中，买单成交额均超过全天所有订单成交额均值的成交金额占比
大单因子：参与成交买卖订单有一方成交额超过全天所有订单成交额均值的成交金额占比。

因子说明

数据：逐笔成交

参考文献

海通证券-20201218-选股因子系列研究（七十一）：逐笔大单因子与大资金行为

转载规则

《股票高频因子》由 Frank Yu 采用知识共享署名 4.0 国际许可协议进行许可。

本篇

股票高频因子

100+ stock factors

2023-07-14 Finance

Stock High-freq factor

python创建环境

Some Posts

2023-06-26