Fixed income securities and markets
What are the fixed income securities?
- A fixed income security is a financial obligation of an entity (the issuer) that promises to pay a specified sum of money on specified future dates
- bond > 10 yr, notes 1-10 yr, bill < 1 yr
- debt obligations and preferred stock
What important information does the indenture contain?
- issue date
- dated date 开始付息日期
- maturity date
- par value
- coupon rate
- covenants,例如不能在creditor不允许的情况下liquidating asset
- redemption provisions and embedded options
- 例如 call,put,convertible
To classify the fixed income securities, can you name the primary securities and derivatives?
- Primary Securities: Treasury bonds, municipal bonds, corporate bonds, ABS
- Derivatives: future/forward, swaps, options
- China classification
- Default-free bonds: government issued, Treasury, municipal, central bank, policy bank, government backed
- credit bonds: financial bond, enterprise, corporate, ABS
Describe the rule of pricing fixed income securities?
- No arbitrage?
- cost nothing but earning a positive profit in a future date
- generate a positive profit at initiation but has sure non-negative payoff in future
- law of one price: securities with identical payoffs should have exact same price
- No arbitrage?
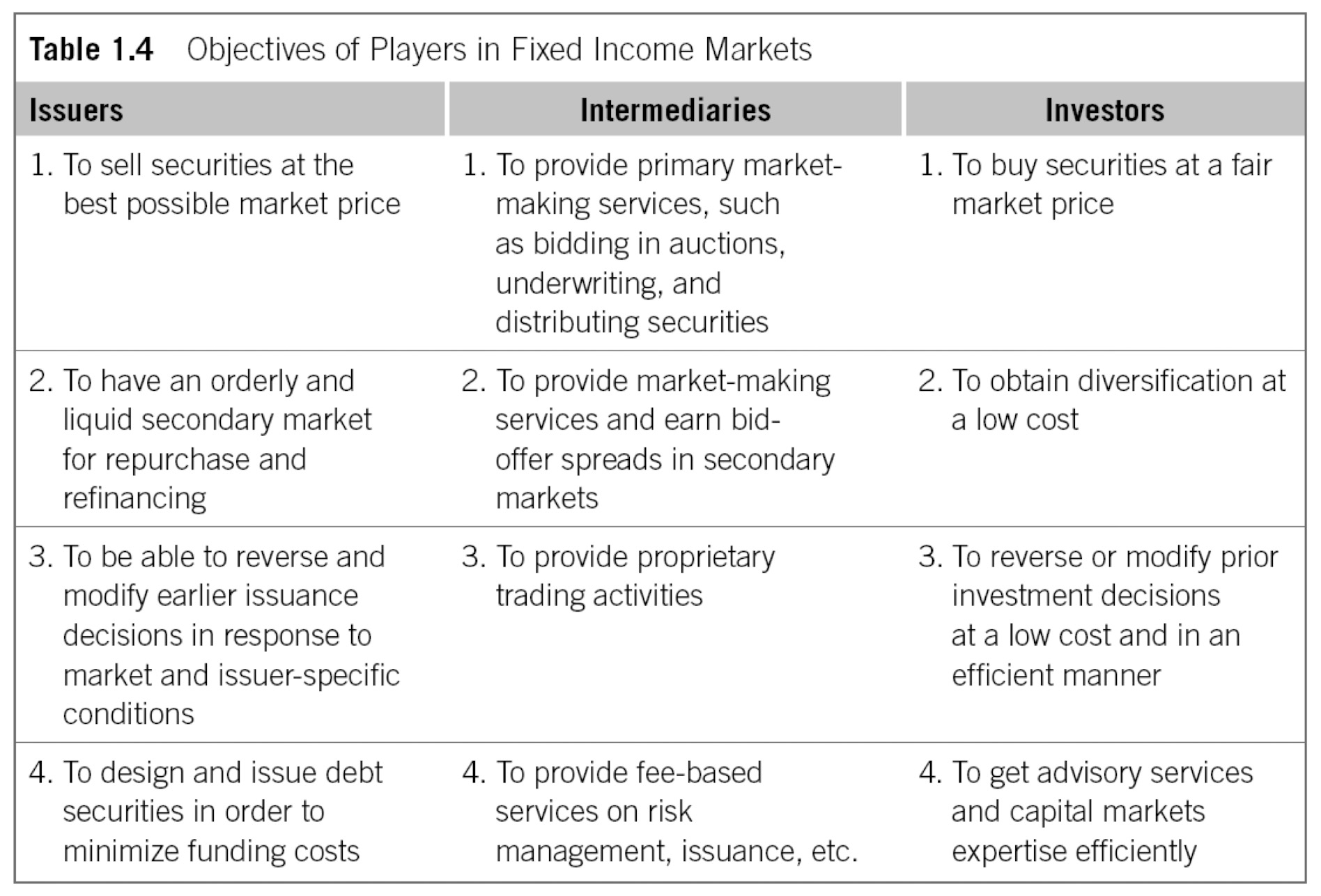
Name the players in the fixed income markets by their roles.
Name the risks embedded in the fixed income markets. Can you explain them in your language?
- interest rate risk
- adverse price movement result from a change in market interest rate. risk that interest rate will rise
- $$Price=\frac{CF}{r},\quad\text{r is the risk}$$
- credit risk
- default risk
- fail to pay
- credit spread risk: reflect how risky the issuer
- different yield between a risky bond and a risk-free bond
- downgrade risk
- default risk
- liquidity risk
- measure: bid-ask spread
- the risk that investor has to sell the bond below its intrinsic value
- the time when this specific is the newest stock means on the run, after its off the run, off off the run
- contractual risk
- due to specific bond contractual features, eg call option
- eg more volatile, call option value inc, price down
- inflation risk
- decline in value of a security’s cash flows due to inflation, measured in purchasing power.
- TIPS, pay real rate
- event risk
- unexpected event, such as natural catastrophe, corporate takeover, regulatory changes.
- volatility risk
- sovereign risk
- exchange rate risk
- reinvestment risk
- the risk that interests and principal pre-payments have to be reinvested at a lower interest rate.
- longer means more risk
- interest rate risk
Fixed income basics
Define simple interest and compounding interest.
- simple interest: interest is calculated based on the outstanding principal amount only.
- compound interest: interest is calculated based on the sum of outstanding principal amount and accumulated interests, that is, interest on interest.
Describe how to price perpetuity, annuity, zero-coupon bond, and coupon bond
- $$FV=PV \times e^{rt}\text{ , }PV=FV\times e^{-rt}$$
- $$P_{perpetuity}=\frac{C}{r}$$
- $$P_{annuity}=\frac{A}{r}[1-\frac{1}{(1+r)^n}]$$
- 两个perpetuity相减
- zero rate一年以内,spot rate推算出来的
- spot rate必须从今天开始
- coupon bond: 对应每个时期的spot rate折现
What is the spot rate?
- Spot (zero) rate is the yield to maturity of a default-free zero-coupon (pure discount) bond.
What is a STRIPS?
- Separate Trading of Registered Interest and Principal Securities
- 例如把一个30-year treasury bond拆成60个coupon payment和一个par payment,就构造了61个新的证券,零息的
The US Treasury bills are quoted in discount yield. How to translate between discount yield and bond equivalent yield?
- $$d=\frac{100-P}{100}\times \frac{360}{n}$$
- $$\color{red}{BEY=\frac{100-P}{P}\times \frac{365}{n}=\frac{365d}{360-nd}}$$
- 这里MAT<182,d是(bid+ask)/2
Describe the relationships between dirty price, flat price, and accrued interest.
- $$\color{red}{P_t^{DIRTY}=P_t^{FLAT}+AI_t}$$
- dirty price is actual pay, flat price is quoted price, difference is accrued interest
What is yield to maturity? Do you understand the relationships between coupon rate, current yield, and yield to maturity for par, premium, and discount bonds?
- YTM, is the discount rate at which the present value of all future promised cash flows of a bond equals its price.
- YTM is bond-specific!
- Assumptions embedded in YTM:
- All cash flows received during the lifetime of the bond are reinvested at the same YTM;
- The bond is held till its maturity.
- current yield = annual interest/market price
- relationship
- For par bond (price = par)
- coupon yield = current yield = YTM
- For discount bond (price < par)
- coupon yield < current yield < YTM
- For premium bond (price > par)
- coupon yield > current yield > YTM
- For par bond (price = par)
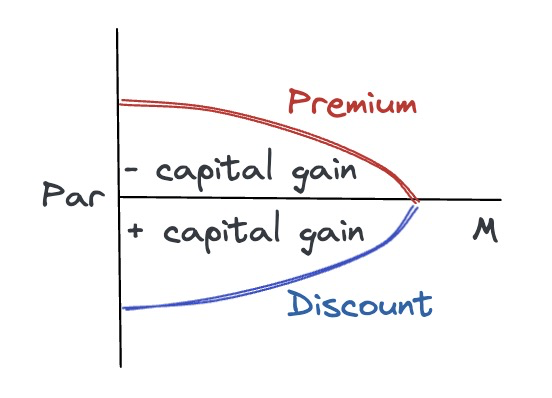
- YTM = coupon yield + capital gain yield
- YTM is not HPR (holding period return)
- 只有当hold the bond to maturity 才是
- bond equivalent yield BEY = annualize quoted yield
- effective annual yield EAY = real yield for one year
- HPR = annual interest/ market price
yield curve
- par yield curve: yield curve for a group of bonds priced at par
- Hypothesis of yield curve
- Expectations theory: 期望理论
- the term structure reflects the market’s expectations of future interest rates.
- Preferred habitat theory:
- different bond investors prefer a particular maturity length over another, and they are only willing to buy bonds outside of their maturity preference if risk premia for other maturity ranges are available.
- Liquidity preference theory: 流动性偏好理论
- investors prefer cash or other highly liquid holdings, suggesting that an investor should demand a higher interest rate or premium on securities with long-term maturities that carry greater risk because, all other factors being equal.
- Market segmentation theory: 市场分割理论
- the market for each segment of bond maturities consists mainly of investors who have a preference for investing in securities with specific durations: short, intermediate, or long-term.
- Expectations theory: 期望理论
Repurchase agreement (repo) and China’s policy interest rate system
Describe repo and reverse repo. What are their functions in the fixed income markets?
- Repurchase agreement (repo) is a contract under which the seller sells a security on the initiation date with an deal to repurchase it at a higher price on a specified later date.
- used to borrow short-term money
- Purpose of reverse repo is to borrow security using cash as collateral, a monetary policy tool, in order to inject liquidity to the market
- Repurchase agreement (repo) is a contract under which the seller sells a security on the initiation date with an deal to repurchase it at a higher price on a specified later date.
Describe special repo versus general repo.
- special repo: the party delivering the security must deliver a specific asset
- general repo: the party can choose among a basket of possible asset
- special repo rate is very low, because the reverse repo side really want it
- trading strategy: lend out special asset, use the money to buy general asset
Describe pledged repo and outright repo in China.
- repo is borrower, reverse repo is lender
- pledged repo
- bonds are used by both trading parties as a pledge of rights
- lender cannot dispose them
- borrower has cash flow rights of the pledged bond
- causing liquidity problem
- outright repo
- positive repo side sell bond to reverse repo
- reverse repo side has the cash flow rights of the pledged bond
- only 10%
Describe China’s policy interest rate system.
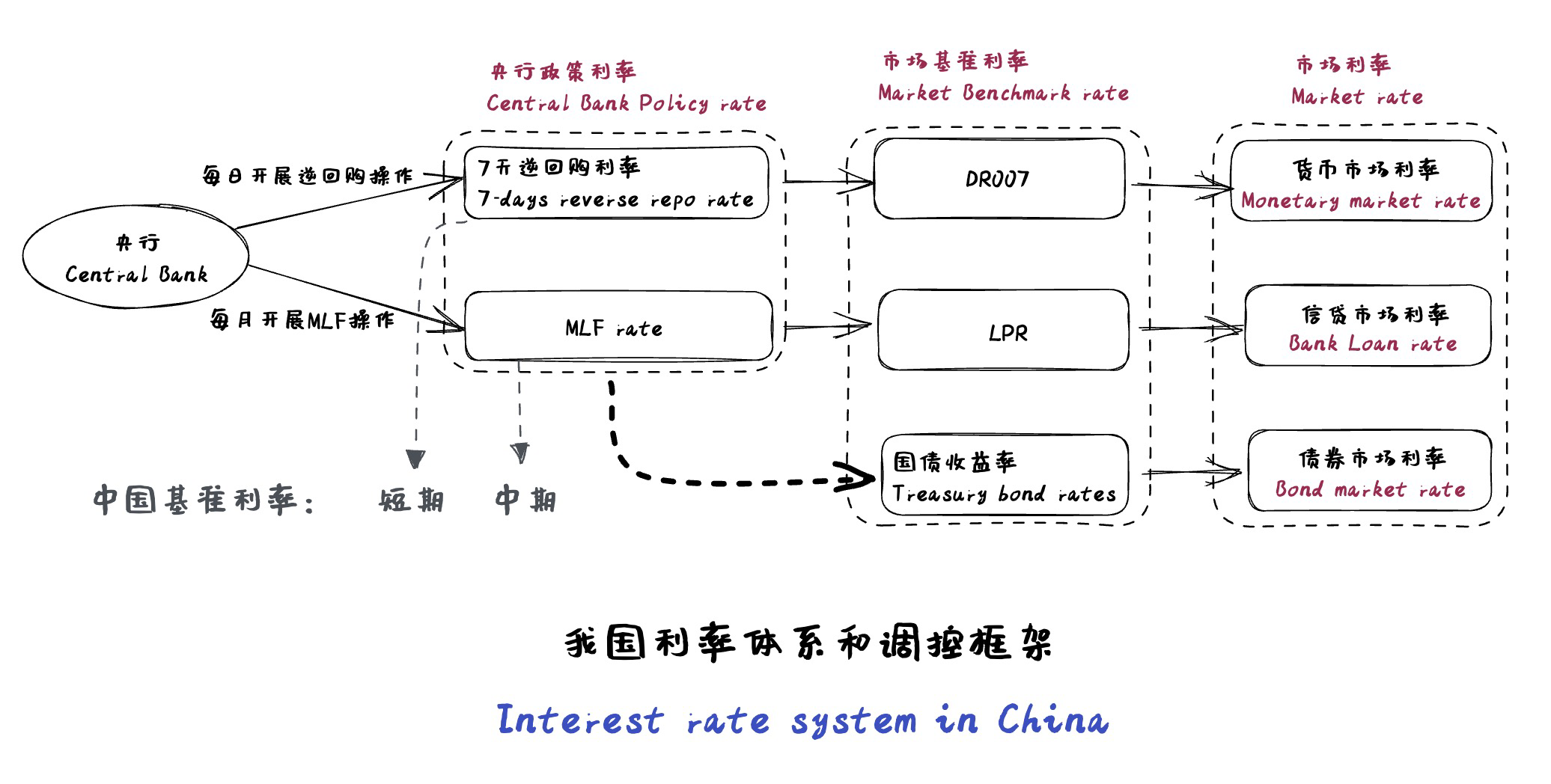
- DR007,7 day repurchase(repo)rate for depositary, central bank policy rate, short-term market benchmark rate
- MLF, medium-term lending facility, PBoC lends to financial institutions through scheduled auctions
- central bank policy rate
- policy and commercial banks participants
- Loan prime rate, LPR, benchmark for bank lending, medium-term market benchmark rate
Describe China’s interest rate corridor.
- the range within which the operating target of the monetary policy–a short-term interest rate – moves around the policy rate announced by the central bank
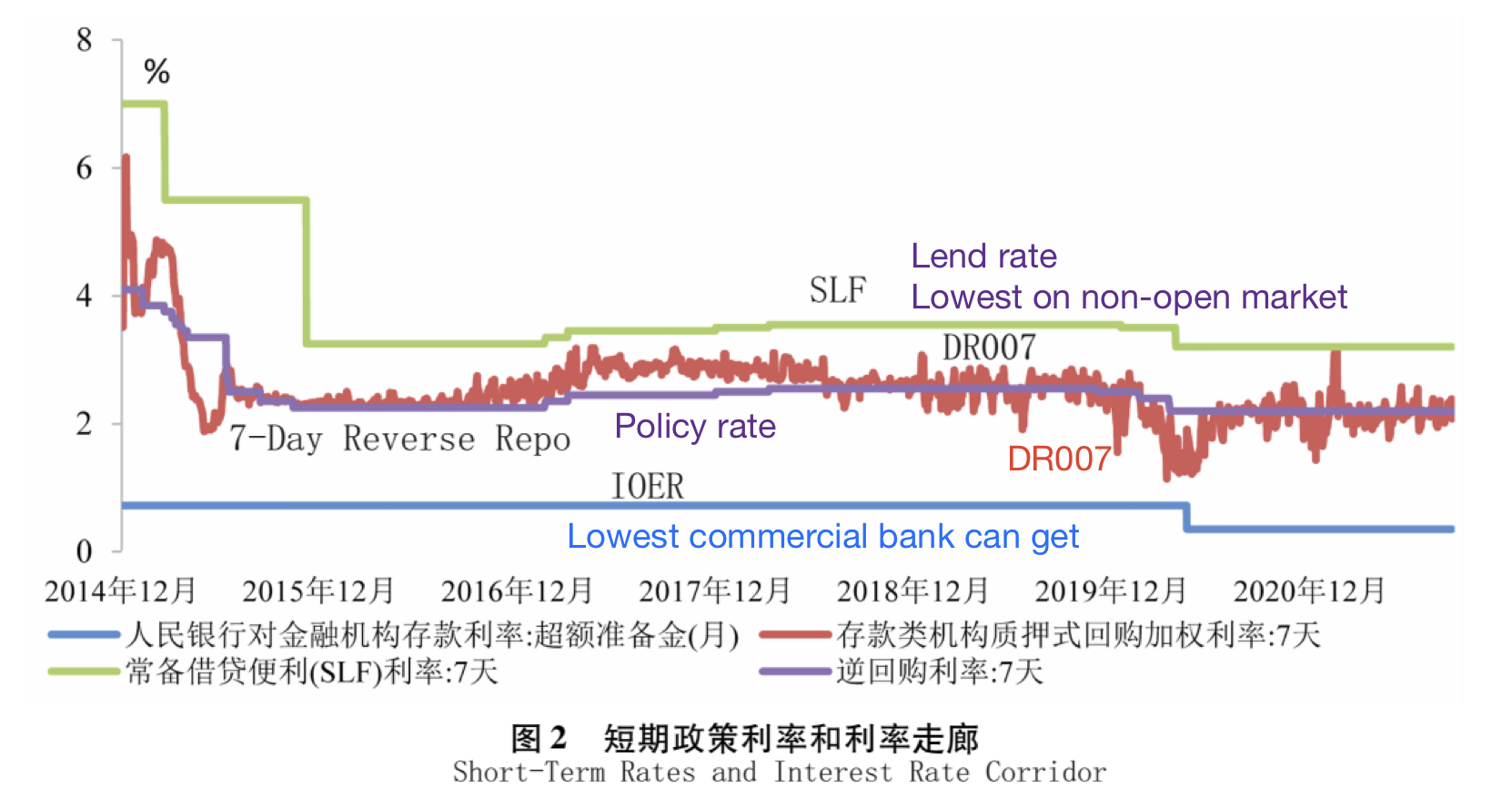
- SLF: standing lending facility, non-open market
- eg commercial bank goes to central bank lending short-term money, having some liquidity problem
- IORB, interest rate on reserve balances, rate of interest central bank pays on reserve balances maintained by depository institutions.
- eg deposit in commercial bank for 100 yuan, commercial bank deposit 11 yuan to central bank.
- IOER, interest rate on excess reserves, beyond 11yuan interest rate.
Treasury securities
Classify China’s Treasury bonds.
- liabilities of central government issued by ministry of finance.
- types
- book-entry, 记账式, for whole-sale
- issued to institution and limited investors, can be traded in secondary market
- primary market tender offer to underwriting syndicate
- secondary market: SSE and SZSE, OTC, interbank and bank counter
- savings, 储蓄式, for retail
- non-tradable
- primary market issued to underwriters(banks)
- book-entry, 记账式, for whole-sale
Describe the issue process of China’s book-entry Treasury bonds.
- tender offer:
- competitive bid: both price and quantity
- non-competitive bid: only quantity, accept price
- typically available for class-A members and for coupon bearing bond with mat less than 10 yrs.
- initially issues of coupon bearing bond uses rate, discounting bond uses price
- bid position:1 basis point or in announcement
- bidding restrictions
- bidding amount:
- max: 35% for A, 25% for B
- min: 4% for A, 1.5% for B
- min underwriting amount:1% for A, 0.2% for B
- rank winning bids: sort by lower rate or higher price, add the amount from the best until market clear. Then before equilibrium price/rate, each get their treasury, at the equilibrium, weighted average by the bidding amount, and give the remaining to the one bids earlier. to two decimal places.
- tender offer:
Describe multiple price/discriminatory auction, uniform price auction, and modified multiple price auction.
- multiple price/discriminatory auction: each winning bid receive the rate it proposes. (American auction)
- uniform price auction: all winning bid receive highest rate that the market clears. (Dutch auction)美国1999年后开始这个
- modified multiple price:rate is weighted average of winning bids. bidding with lower rate pay par price, bidding with higher rate pay discount price(with regard to their bidding rate)
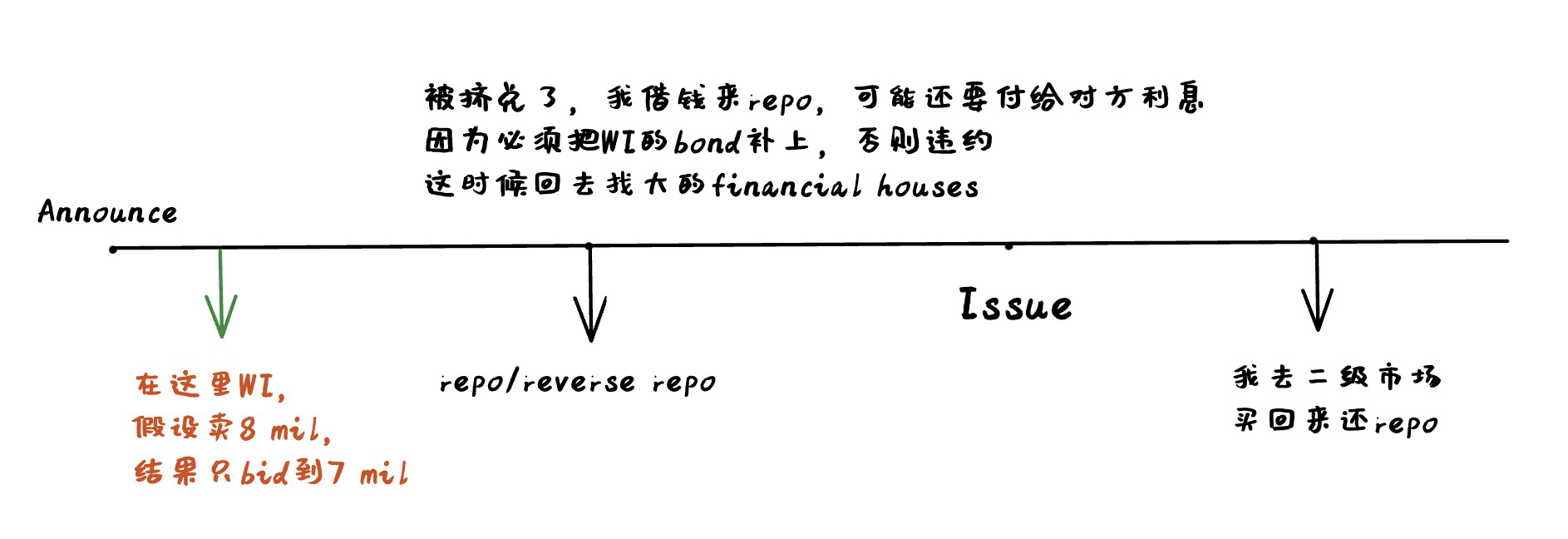
Describe when-issued (WI) trading. What are the benefits of WI trading?
- When-issued (WI) is a transaction or trade in securities that are not yet issued, on the understanding that the trade will be settled once the securities are issued.
- occurs between announcement date and issue date
- special kind of future for non-existing securities
- benefit:
- information discovery, known what the investor want for interest rate and quantity.
- downside:
- short squeeze
- repo specialness
What does short squeeze mean?
Duration and convexity
Describe the price-yield relationship.
- inverse convex relationship between price and yield. negative correlated
Define and explain duration. What bond features affect duration?
- Duration is its discounted-cash-flow-weighted time to receipt of all promised cash flows divided by its price.
- loosely speaking: average time to receive all the cash flow.
- $P=\sum_{i=1}^NC_ie^{-yt_i}$, duration is expressed as
- $$D=\frac{\sum_{i-1}^NC_ie^{-yt_i}\times t_i}{P}$$
- no unit
- duration is interest rate risk measure.
- modified duration: $$MD=-\frac{\frac{\partial P}{P}}{\partial y}\approx -\frac{dP/P}{dy}$$
- $$D^{Macaulay}=-\frac{dP/P}{d(1+y)/(1+y)}=-\frac{dP/P}{dy}(1+y)$$
- features affect duration
- Maturity: Longer-term bonds have higher duration than shorter-term bonds.
- Coupon rate: Bonds with lower coupon rates have higher duration than bonds with higher coupon rates.
- Yield: Bonds with lower yields have higher duration than bonds with higher yields.
- Call provisions: Callable bonds have lower duration than non-callable bonds.
- Put provisions: Bonds with put options have higher duration than bonds without put options.
- Credit quality: Lower-rated bonds have higher duration than higher-rated bonds.
- Coupon frequency: Bonds with more frequent coupon payments have lower duration.
- Yield curve: Bonds with flatter yield curves have higher duration than bonds with steeper yield curves.
Describe price value of one basis point (PVBP/DV01). What is the relationship between duration and PVBP?
- change in the price due to a change in interest rate
- $$PVBP=\frac{\partial P}{\partial y}=\sum_{i-1}^NC_ie^{-yt_i}\times t_i=DP$$
Describe the properties of duration.
- A zero-coupon bond’s duration equals its maturity, implying that the zero-coupon bond is the most interest-rate-elastic instrument for a given maturity.
- A coupon bond’s duration is less than its maturity.
- Duration increases with maturity.
- Duration decreases with coupon rate and yield to maturity.
- Duration is time-varying.
- As a linear approximation of the price-yield relationship, duration may not work well for significant shifts in the term structure.
- Duration works only for parallel shifts in the term structure and may fail miserably if the term structure tilts while shifting parallelly.
Describe the logic behind duration hedging and the spread trading strategy?
- changing slope of the term structure.
- need curvature change
- expect the yield curve steepen
- bearish market, long term rates goes up more
- bullish market, short rates fall more
- construct a duration neutral long short position
- long the short-term bond and short the long-term bond
- $n_1\times PVBP_1=n_2\times PVBP_2$
- main reason this doesn’t work very well in real world is because of bid-ask spread
Describe dollar convexity and relative convexity.
- $$$Conv=\frac{\partial^2P}{\partial y^2}=\sum_{i=1}^NC_ie^{-yt_i}(t_i)^2$$
- $$RConv=\frac{$Conv}{P}=\frac{\frac{\partial^2P}{\partial y^2}}{P}$$
- Convexity is the change in the slope of the price-yield curve for a slight change in the yield.
- $$\color{red}{\frac{dP}{P}=\frac{\frac{\partial P}{P}}{\partial y}dy + \frac{\frac{\partial^2P}{\partial y^2}}{2P}(dy)^2}$$
- for zero coupon bond, RConv is t-square
- positive convexity is desired, because second term in formula is always positive
What bond features affect convexity?
- convexity is the change in the slope of the price-yield curve for a slight change in the yield.
- the more convex a bond price is, the more valuable the bond is
- The main bond features that affect convexity are:
- Coupon rate: Bonds with lower coupon rates have higher convexity than bonds with higher coupon rates.
- Maturity: Longer-term bonds have higher convexity than shorter-term bonds.
- Yield: Bonds with lower yields have higher convexity than bonds with higher yields.
- Call provisions: Callable bonds have lower convexity than non-callable bonds.
- Put provisions: Bonds with put options have higher convexity than bonds without put options.
- Credit quality: Lower-rated bonds have higher convexity than higher-rated bonds.
- Volatility: Bonds with higher volatility have higher convexity than bonds with lower volatility.
What securities have negative convexity? Why?
- Bullet bond often have positive convexity
- Callable bonds usually exhibit negative convexity at lower yields. The price of a callable bond might drop as the likelihood that the bond will be called increases, and the shape of a callable bond’s curve of price to yield is concave or negatively convex.
- Most mortgage securities exhibit negative convexity due to the mortgage borrower’s incentive to refinance at a lower rate when market yields decline.
Describe the butterfly trading strategy. What risks is it exposed to?
- establishing a duration-neutral strategy, but relative convexity is positive.
- short the middle term and long the short and long term.
- Underlying, it is trading flattening. If it goes flattening, it will be more earning.
- See as two spread trading composed.
- the first is short the long and long the short, will earn if steepening
- the second is short the short and long the long, will earn if flattening
- because of curvature, second earns more than the first one lose
- need curvature change
Constructing the term structure
For pricing, we need to have the term structure of spot rates. We apply bootstrapping and interpolation to construct it.
- bootstraping: self-starting process without external inputs
- interpolation: using given points to estimate unknown points
Describe bootstrapping. How to apply it?
- given observed market data, can compute other points in the term structure.
Describe interpolation and name the approaches. Do you know how to apply them?
- Linear interpolation
- Non-Linear
- Nelson-Siegel & Nelson-Seigel-Svensson
- pro: fewer parameters, easy to implement
- con: less precise
- beta0: level component, long-term rate
- beta1: slope component, downward when > 0
- beta2: curvature component, hump when > 0
- tao1: shape
- Splines-based model
- pro: precise fit
- con: more parameters
- Nelson-Siegel & Nelson-Seigel-Svensson
Do you know how to construct a forward curve from the spot curve (or based on zero prices)?
- $$(1+s_n)^n=(1+f_{0,1})(1+f_{1,2})(1+f_{2,3}) \ldots(1+f_{n-1, n})$$
- $$(1+f_{m, n})^{n-m}=\frac{(1+s_n)^n}{(1+s_m)^m}$$
Implications, layers
- Pure Expectations Hypothesis, PEH
- implied spot rates one year forward will realize over next year.
- all government bonds have same near-term expected return reagrdless of maturities
- Risk Premium Hypothesis, RPH
- forward rate reflects a bond’s expected return
- no expected change in spot rates
- n-year bond will receive a one year return $f_{n-1,n}$
- Convexity Bias
- Convexity-Adjusted Expected return = rolling yield + convexity value
- rolling yield = $f_{n-1,n}$
- Convexity value $\approx -0.5\times convexity\times (Vol(\Delta y))^2$
- Putting together
- $\text{Rolling Yield} =\text{Short-Term Rate} + \text{Bond Risk Premium} + \text{Duration} \times E(\Delta s_{n-1})+ \text{Convexity Bias}$
- Pure Expectations Hypothesis, PEH
Interest rate modeling
Describe the standard and general Wiener processes.
- standard Wiener process
- $\Delta W=\varepsilon \sqrt{\Delta t}$, where $\varepsilon$ is a random draw from a standard normal distribution $N(0,1)$;
- the values of $\Delta W$ in two different time intervals are independent.
- $E[W(T)-W(t)]=0$, $V A R[W(T)-W(t)]=T-t$
- general Wiener process
- $$\Delta x=\mu \Delta t+\sigma \Delta W=\mu \Delta t+\sigma \mathcal{E} \sqrt{\Delta t}$$
- where the drift $\mu$ and the volatility $\sigma$ can be constants.
- $E[\Delta x]=\mu \Delta t$, $Var(\Delta x)=\sigma^2 \Delta t$
- build a realistic model to describe the underlying source of risk
- provide probability distribution of outcomes at an important future time
- standard Wiener process
Why do we need to specify the short rate process in interest rate modeling?
- to better describe fixed income securities whose cash flow depend on future movements of interest rate.
- reflect real interest rate fluctuation
- model provide the prob. distribution of outcomes at important future time, which then can be used to compute expected value
Describe the desirable properties of an interest rate model. Can we have all of them in one single model? If not, how should we make the trade-off?
- Economic soundness: non-negativity of interest rate, mean reversion.
- Reasonable distribution of spot rates at given maturity
- correlation structure between interest rate of different mat.
- volatility structure of interest rate
- tractability: analytical solution
- tradeoff:
- depend on application.
Describe the main characteristics of the Vasicek model and Cox-Ingersoll-Ross (CIR) model. What are their pros and cons?
- Vasicek:
- short rate follow Brownian motion, $dr_t=\kappa (\mu - r_t)dt+\sigma dW_t$
- mean reversion, allow negative interest rates
- zero coupon bond price can be priced
- calibrate model to estimate coefficient and apply to other bond
- Main character
- Continuous time one factor model
- Allow negative interest rates
- simple, closed-form solution
- Not for perfect calibration
- Vasicek: short rate – underlying bond – price of option
- CIR:
- short rate follow Brownian motion, $dr_t=\kappa (\mu - r_t)dt+\sigma \sqrt{r}dW_t$
- mean reversion, no negative interest rates
- zero coupon bond price can be priced
- Main character
- Continuous time one factor model
- No negative interest rates
- simple, closed-form solution
- Not for perfect calibration
- They have closed-form solution, but not very precise.
- Vasicek:
The Black-Derman-Toy model perhaps is the most popular interest rate model. Can you describe how to apply it to price the options attached to a bond?
- if short rate follow Geometric Brownian motion, $$dlnr(t)=[\theta (t)-\frac{\partial \sigma (t)/\partial t}{\sigma (t)}lnr(t)]dt+\sigma (t)dW_t$$
- then, $r(t+1)=r(t)e^{\theta \pm \sigma}$
- if short rate follow Brownian motion,
- $$r(t+1)=r(t)+\theta \pm \sigma$$
- $$\frac{R(t+1,j+1,T)}{R(t+1,j,T)}=e^{2\sigma_R(t,T)}$$
- using bivariate lattice to price options
- calculate value of the option in every scenario and discount to time 0
- American option need to consider one more thing, continuation value
- model is callibrated to market yields and volatilities
- if short rate follow Geometric Brownian motion, $$dlnr(t)=[\theta (t)-\frac{\partial \sigma (t)/\partial t}{\sigma (t)}lnr(t)]dt+\sigma (t)dW_t$$
Describe analytical solution versus numerical solutions (binomial tree and Monte Carlo simulation). What are their advantages and drawbacks?
- with tree, can estimate discount bond price, spot rate, forward rate, interest rate derivative price
- numerical are much more time and space consuming.
Interest rate derivatives
Describe interest rate swap (IRS). How to compute the fixed rate of an IRS? We have introduced two approaches in class.
- life of an IRS is called swap term
- if payments are made at the end of the period, it is said to be settled in arrears
- payer is payer of the fixed rate
- receiver face greater interest rate risk, because receiver is essentially holding a long term bond
- first payment date = second reset date
- compute fixed swap rate:
- first way, hedged swap have 0 NPV
- $$\sum_{i=1}^NP(0,t_i)[R-r_0(t_{i-1},t_i)]=0$$
- $$R=\sum_{i=1}^N[\frac{P(0,t_i)}{\sum_{j=1}^NP(0,t_j)}]r_0(t_{i-1},t_i)$$
- weighted average of floating rate
- second way, for par coupon bond
- $$\sum_{i=1}^NP(0,t_i)R+P_0(0,t_n)=\sum_{i=1}^NP(0,t_i)r_0(t_{i-1},t_i)+P_0(0,t_n)=1$$
- $$R=\frac{1-P_0(0,t_n)}{\sum_{i=1}^NP_0(0,t_i)}$$
- who pays who? earning less pays to earning more, and eliminate the swap.
- swap spread: the spread between fixed rate and YTM of underlying treasury
Describe forward and futures contracts. What are the key differences between them?
- forward contract is an agreement entered by two parties. One agree to buy, the other agree to sell an underlying asset at a predetermined price on a specified date in future.
- on the settlement date, the seller is obligated to deliver the asset, price at forward price.
- assigned between two parties
- no cash flow between signing day and delivering day
- Futures are similar to forward, agreement on deliver some asset to the other party on the settlement date on the agreed price.
- marking to market, effectively rewrite the contract every day
- doing so in exchange market.
- have regulations
- trade via margin
- highly liquid
- broker account change every day
- Financial futures: stock index futures, interest rate futures, currency futures
- forward contract is an agreement entered by two parties. One agree to buy, the other agree to sell an underlying asset at a predetermined price on a specified date in future.
Describe conversion factor CF.
- conversion factors link the different prices of the eligible bonds and the price of a reference bond. because future prices are quoted on a reference bond with same maturity.
- each bond have a unique conversion factor.
- Delivery bond price = CF ✖️ Reference bond price
- CF does not change over time.
Describe the options embedded in a Treasury futures contract.
- Quality: can deliver any eligible bond–cheapest to deliver
- timing: delivery notice can be given in a period, not only on a month.
- wildcard: future exchange close early, but bond keep trading.
- end-of-month: future trading stop before the end of month.
What is the cheapest-to-deliver (CTD) bond? How to determine the CTD bond?
- when delivery occurs, it is the choice of seller to determine which eligible bond to deliver.
- the bond that is the most economical for the shorter.
- 3 ways to characterize CTD:
- CTD has cheapest forward invioce price
- It has highest implied repo rate(IRR)
- which is the theoretical rate of return the short could earn by purchasing the cash security and delivering it into futures contract.
- It has lowest basis after carry or net basis.
- $Basis=P_t - CF\times F_t$
- 现货和期货的价差, $F_t$ 是远期价格
- $Carry=[AI_T-AI_t]-(P_t+AI_t)\times r\times \frac{T-t}{360}$
- 期货和现货的利息差,第一项是interest income,第二项是interest cost
- $BAC\approx \text{Option Value}$
- $Basis=P_t - CF\times F_t$
Describe the call (put) option on a futures contract.
- Call option
- the buyer has the right but not obligation to purchase
- the seller has an obligation to sell upon exercise of the call
- Put option
- the buyer of a put option has the right but not obligation to sell
- the seller of put option has responsibility to buy upon exercise
- European option: only exercised at the expiration date
- American: exercised at any time up to expiration date
- Bermudan and Atlantic: before expiration date, but only certain date.
- Call option
Credit risk and derivatives
Describe default, financial distress, workout, bankruptcy, and their relationships.
- default: failure to meet the legal obligations of a loan
- financial distress: its liquid assets are not sufficient to meet the requirements of its obligations(before default)
- solutions
- restructuring assets: asset sales, fire sales, carry along with financial restructuring
- private workout: debt restructuring to reduce par, extend maturity, debt fot equity swap
- workout means the company is in financial distress, fundamentally good, while if no need to workout means it is in economic distress and is fundamentally bad
- solutions
- bankruptcy: when workout fails, defaulted firm enter into bankruptcy. It is a legal status of a person or entity cannot repay its debts
- Chapter 7: liquidation, sale of nonexempt property and distribution of the proceeds to creditors.
- Chapter 11: reorganization, debtor remain in possession, but creditors have some power.
Credit rating:
- Describe the rating grades.
- shows the probability that a firm may default
- What is the threshold between the investment and speculative (“junk”) grades?
- for Moody’s, Baa3 and above is investment, Ba and below is junk
- for Std Poor’s, BBB- and above is investment, BB+ and below is junk
- Describe the key features of Chinese domestic agency ratings.
- almost no A- and below, tend to report very good
- only AAA can be public fund.
- cliff downgrading often occur.
- upgrade more than downgrade
- underestimate the default risk
- issuer paid rating is higher than investor paid ratings
- Describe the rating grades.
How do we quantify credit risk? What are the drivers for credit spread?
- using credit spread
- credit spread is typically viewed as the difference between YTM of a risky security and the YTM of a treasury with same maturity.
- core component
- probability of default PD
- expected loss in the event of default LGD
- drivers
- high risk require high return
Describe the credit scoring model. What are the pros and cons of it?
- Altman’s Z-score model
- short-term liquidity, internel growth potential measure, profitability, leverage, efficiency
- pro
- easy to estimate
- empirical results are good
- limitations
- theoretical foundation is poor
- frequency of data needed
- Impact of different industry and general economic situation
- Nonlinearity of impact of credit factors on default prob.
Describe the dynamics of a structural form model of credit risk, e.g., as in Merton (1974).
- equity is analogous to a call option on the firm’s assets
- debt is analogous to a risk free bond and a short put option
- suppose firm value $v_T$, bond par K, then bond price $B_T=v_T-E_T=K-max(K-v_T,0)$
- Call-Put parity
- $P+S=C+Xe^{-rT}$
- P is European put, S is underlying asset, X is strike price
- $V=C+Fe^{-rT}-P$
- C is equity, latter is Debt
- using BS model to get this model
Describe Moody’s KMV’s EDF.
- EDF means expected default frequency: prob. that a firm will default within a given time horizon.
- current EDF = 2% means it has 2% prob. to default in next 12 months
- KMV’s EDF provide 5 years
- EDF range from 2 to 2000 basis point
How to estimate distance-to-default? Can you outline how KMV maps distance-to-default to EDF?
- In structural models, value of a firm is described by a GBM diffusion process, suppose liability F have to be repaid at T
- Distance-to-Default DD is $$X_t=\frac{ln(v_t/F)}{\sigma}$$
- KMV uses actual default rates for companies in similar risk ranges to determine a functional relationship
- for similar DDs, form a group, see how many default in 1 year, in 2 years, …
Describe the dynamics of a reduced form model of credit risk, and discuss its difference from the structural form model in mechanism and application process.
- risk-neutral default prob. is modelled directly as an exogenous random cariable
- intensity of default $\lambda$ , suppose follow a Poisson process
- $$Q(t)=E[e^{-\int_0^t \lambda(u) d u}]$$
Describe credit default swap (CDS). Can you outline how to price a CDS?
- CDS is an OTC contract that allows one party to sell default insurance on a debt obligation(reference obligation)to another party
- typically triggered by credit events
- bankruptcy;
- failure to pay outstanding debt obligations
- obligation default;
- obligation acceleration(others default, causing this one quicker.)
- repudiation or moratorium(delay,withhold payment)
- restructuring of a loan or the bond of the reference entity including the reference obligation.
- pricing CDS
- $$NPV^{\text {premia }}=\sum_{i=1}^n \frac{s}{2} \times N \times e^{-r_i t_i} \times Q(\tau>t_i)$$
- $$NPV^{\text {default }}=\sum_{i=1}^n(1-R) \times N \times e^{-r_i t_i} \times Q(\tau=t_i)$$
- $$\frac{s}{2}=\frac{\sum_{i=1}^n(1-R) \times N \times e^{-r_i t_i} \times Q(\tau=t_i)}{.\sum_{i=1}^n N \times e^{-r_i t_i} \times {Q(\tau>t_i)}}$$
- using reduced form or structural form model to get Q