Overview
金融Finance:optimally allocate financial resourses, in the presense of uncertainty.
给分
- 作业:30
- 小组展示,30min,20
- 期末,50
L1: Fixed Income Securities and Markets
金融产品分类
primary assets: equity, fixed income securities (bond), foreign exchange (currency), commodity, real estate
derivatives: forward, swap, option.
fixed income security
defination: A fixed income security is a financial obligation of an entity (the issuer)
that promises to pay a specified sum of money on specified future dates
category
- debt
- bonds: > 10 yrs(国内5年以上)
- notes: 1 - 10 yrs(国内1-5年)
- bills: < 1 yr
- preferred stocks
- have debt-like feaures
indenture 契约
elements
- issue date:发行日期
- dated date:开始付息日期
- maturity date:到期日
- par value: 面值
- par 100,discount<100, premium>100
- coupon rate:固定日期付息
- coupon rate = coupon / FACE value
- fixed-rate
- TIPS
- treasury inflation protected seminally,fixed-rate but not fixed payment
- 根据CPI定利息
- TIPS
- floating-rate
- DR007:银行间存款类金融机构以利率债为质押的7天期回购利率,基准利率
- zero: 贴现
- step-up: 越来越高
- deferred coupons: 延后
- covenants:约定
- affirmative covenants
- negative covenants
- 对于borrowers的行为进行限制和约束,例如不能在没有creditor允许的情况下liquidating asset
- Redemption provisions and embedded options
- Bullet maturity: 在到期日之前不需要还任何principal
- Amortizing securities:例如房贷
- sinking fund provision:在债券到期之前定期偿还本金
- call provision: issuer可以随时召回,更便宜
- price = price regular - value of the call
- put provision: bondholder可以随时卖出,更贵
- price = price regular + value of the put
- convertible bond: 可以把债转成common stock
债券分类
China
- Default-Free Bonds(no default risk)利率债
- Treasury Bonds 国债,财政部印发
- Municipal Bonds 地方政府债
- Central Bank Bills 央票
- 用来调整市场流动性,短期
- Policy Bank Financial Bonds 政策银行金融债(政金债)
- 国家开发银行
- 中国农业发展银行
- 中国进出口银行
- Government-Backed Bonds 政府支持机构债券
- 中国国家铁路集团有限公司
- 中央汇金投资有限公司(Shareholding Company)
- Credit Bonds 信用债
- Financial Bonds 金融债
- Issued by Commercial Banks 商业银行债
- Issued by Non-Bank Financial Institutions 非银行金融机构债
- Enterprise Bonds 企业债
- governed by the NDRC, including “ChengTou” Bonds 发改委审批,包括城投债
- municipal corporate bonds
- governed by the NDRC, including “ChengTou” Bonds 发改委审批,包括城投债
- Corporate Bonds 公司债
- governed by the CSRC 证监会审批
- SME Collective Bonds 中小企业集合债
- issued under one name, small and medium enterprises
- Debt Financing Instruments of Non-Financial Enterprises 非金融企业债务融资工具
- Commercial Papers 短期融资券 < 1 year
- Super Short-Term Commercial Papers 超短期融资券 < 9 months
- Medium-Term Notes 中期票据 typical 3-5 years
- SME Collective Notes 中小企业集合票据 < 5 years
- Asset-Backed Securities(ABS)资产证券化
- Originated by Financial Institutions 信贷资产支持证券
- Originated by Enterprises 企业资产支持债券
- Securitization: 把不流动性资产换成流动性资产
- Financial Bonds 金融债
债券市场
China
- Primary Markets 一级市场 (Issuers)
- Public Issuance 公募发行
- Tender Offer / Auction 招标发行,拍卖(例如treasury bond)
- Book Building and Underwriting 簿记建档发行
- Private Placement 协议定向发行(私募)
- Bank Counter 柜台发行
- 例如saving treasury bonds 储蓄式国债
- Public Issuance 公募发行
- Secondary Market (Investors)
- OTC (Over the counter)场外市场
- Interbank bond market 银行间债券市场
- regulator: PBOC
- 上海清算所
- Commercial Bank Counter 商业银行柜台
- Interbank bond market 银行间债券市场
- Exchange 场内市场(交易所)
- No commercial bank
- SH, SZ, (BJ)
- OTC (Over the counter)场外市场

Players in Fixed income markets
| Issuers | Intermediaries | Investors |
|---|---|---|
| Governments and their agencies | investment banks | governments and sovereign wealth funds |
| corporations | Commercial Banks | Pension funds |
| Commercial banks | Dealers | Insurance companies |
| States and municipalities | Primary dealers 大做市商 | mutual funds |
| Special-purpose vehicles(SPVs) | Interdealer brokers | Commercial Banks |
| Foreign Institutions | credit-rating agencies | asset manaement firms |
| Households |
- 注:
- Foreign Instutions
- 外资在中国发RMB债叫 panda bond
- 在香港发港币债叫 dim sum bond
- 在JAPAN 发 YEN 债叫 warrior bond
- 在 US 发 USD 债叫 yankee bond
- SPV:issuers of ABS
- Foreign Instutions
Risk of bonds
interset rate risk
- negative relation
- typically the risk that the interest rate will rise
- $P_{price}=\text{cash flow}/r$
credit risk
- default risk: fail to pay, risk of the buyer
- credit spread risk: difference between yield of risky bond and risk free bond, reflect the risk level of the issuer
- downgrade risk: 评级变化(AA->BBB)
- solution
- third-party garrantee
- sinking fund
liquidity risk
- measure: bid-ask spread
- from the perspective of dealer
- bid: price the dealer wants to buy
- ask: price the dealer willing to sell
- ask > bid
- if spread is huge, liquid is small.
- from the perspective of dealer
- OTC
- measure: bid-ask spread
Contractual risk
- embedded call option
- interest rate dec., more likely to call back and issue new one, price of call option inc., and price of bond dec.
- embedded call option
Inflation risk
- PV贬值风险
- TIPS,与CPI挂钩
Event risk
- The risk that an issuer’s ability to make interest and principal payments changes dramatically and unexpectedly because of certain events such as a natural catastrophe, corporate takeover, or regulatory changes.
- In October 1988, RJR Nabisco was taken over through LBO(Leverage buyout),’Moody’s rating of RJR Nabisco’s debt went from A1 to B3. The Prices of RJR bonds dropped about 15%.
- borrow debt to retire equity
- 加杠杆
- Solution: super-poison put provision.
- 强制触发put option
Volatility risk
- the risk that the price of a bond with an embedded option will decline when expected yield volatility changes.
- 如果预期下个月的利率会变的volatile,call option and put option 都会升值
- option的价值与volatility 直接相关
Sovereign risk
- the risk that a foreign government’s actions cause a default or price decline on its bond issues.
Exchange rate risk
- the risk that the currency in which the interests and principal payments are denominated will decline relative to the investor’s domestic currency.
Reinvestment risk
- the risk that interests and principal pre-payments have to be reinvested at a lower interest rate.
- 时间越长,风险越高
L2: Basics
basic terms
- Bid price: the price at which a dealer is willing to purchase
- Ask/offer price: the price at which a dealer is willing to sell
- One basis point = 0.01 percentage point; that is 100 bps = 1%
- Tick price-one tick usually equals 1/32 of a dollar, e.g., 98.22+,103.05++
- old market convention
- 103.05++ = 103 + 5/32 + 1/64 + 1/128
- Yield to maturity (YTM), or yield, is the discount rate at which the present value of all future cash flows equals bond price
- IRR asumption
- all future cash flow will be reinvested in the same yield
- project will not obsolete before it is done
- IRR asumption
Interest rate
Simple interest
- interest is calculated based on the outstanding principal amount only.
- Simple interest applies to repurchase agreements (repos) and other money market instruments.
- $$FV = PV(1+r*\frac{t}{365})$$
- r 是年化利率
Compound interest
- interest is calculated based on the sum of outstanding principal amount and accumulated interests, that is, interest on interest.
- In general, m-ly compound for n years
- $$FV=PV(1+\frac{R}{m})^{n\times m}$$
- 对于连续复利
- $$FV=PV exp^{rt}$$
- 计算方便
- 转换:
- $$(1+\frac{R}{m})^{n\times m}=exp^{rt}\text{ , thus } r=m*ln(1+\frac{R}{m})\quad \text{, thus } R=m(e^\frac{r}{m}-1)$$
Pricing basic securities
- Perpetuity
- $$P_{perpetuity}=\frac{C}{r}$$
- A security that pays A (dollars) per period for n periods is known as annuity, e.g., a mortgage.
- If the first payment occurs one period from now, it is called ordinary annuity;
- $$P_{annuity}=\frac{A}{r}[1-\frac{1}{(1+r)^n}]$$
- if the first payment happens now, it is called annuity due.
- If the first payment occurs one period from now, it is called ordinary annuity;
Zero-coupon bond
- Treasury bills (T-bills) are zero-coupon instruments, but their maturities are no more than one year.
- How to obtain zero-coupon bonds of longer maturities?
- In the U.S., STRIPS (Separate Trading of Registered Interest and Principal Securities) are the registered interest and principal components of a coupon bond (fixed-rate T-bond or T-note) in the Federal Reserve Banks’ book-entry system.
- A 30-year Treasury bond can be separated into 61 STRIPS: 60 semiannual coupons plus a single face value payment.
- The one original security is now 61 separate new securities with unique Committee on Uniform Securities Identification Procedures (CUSIPs).
- 把treasury bond的coupon折价卖掉,构造更长期的零息债券
- In the U.S., STRIPS (Separate Trading of Registered Interest and Principal Securities) are the registered interest and principal components of a coupon bond (fixed-rate T-bond or T-note) in the Federal Reserve Banks’ book-entry system.
- STRIPS are effectively zero-coupon bonds (zeroes).
Price zero-coupon bonds
- Spot (zero) rate is the yield to maturity of a default-free zero-coupon (pure discount) bond.
- Although used interchangeably, zero rates mainly refer to rates with maturities less than one year, where real zero-coupon bonds exist.
- Spot rates are associated with maturities above one year and typically “implied.” 长期,推算出来的。
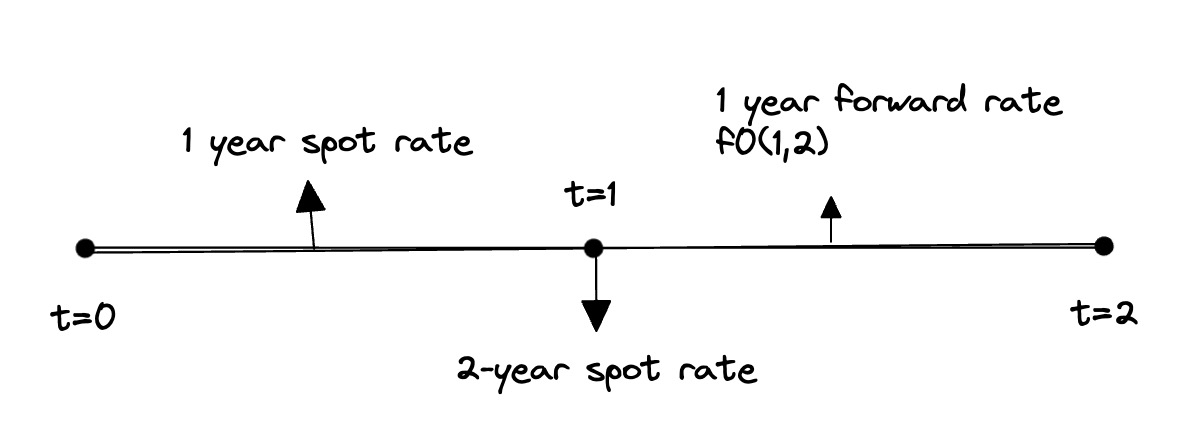
- spot rate 必须从今天开始
Pricing rule in fix-income securities
No arbitrage
An arbitrage opportunity is a feasible trading strategy involving two or more securities with either of the following characteristics:
- It does not cost anything at initiation but generates a sure positive profit by a certain date in the future;
- It generates a positive profit at initiation but has a sure nonnegative payoff by a certain date in the future.
The no-arbitrage condition requires that no arbitrage opportunities exist.
The law of one price establishes that securities with identical payoffs should have the same price.
- not expected, but exact same payoff!!
Pricing in Practice
US T-bills are quoted on a discount yield basis
- $\color{red}{\text{bid yield is higher than ask yield}}$
- 与price相反
- $$P=100(1-\frac{nd}{360})$$
- d is the discount yield, n is number of days between settlement and maturity date.
- $\color{red}{\text{bid yield is higher than ask yield}}$
Due to US convention, discount yield is expressed as
- $$d=\frac{100-P}{100}\times \frac{360}{n}$$
- quoted yield is not real yield.
Bond equivalent yield of MAT < 182 days is
- $$\color{red}{BEY=\frac{100-P}{P}\times \frac{365}{n}}$$
- 思路:profit/price,than annualize, and make it daily.
- d 使用(bid+ask)/2
- BEY 总是比 discount yield 大
Bond equivalent yield of MAT > 182 days
- assume interest y is paid after 6 months and reinvested
- $$P(1+\frac{y}{2})+\frac{y}{365}(n-\frac{365}{2})(1+\frac{y}{2})P=100$$
- y is equivalent yield.
- assume interest y is paid after 6 months and reinvested
Invoice price
- Most bond transactions occur between two coupon dates.
- Bonds are usually quoted on a flat/clean price basis.
- 中美都是
- Accrued Interest = coupon * time from previous coupon date
- Full/invoice/dirty price
- $$\color{red}{P_t^{FULL}=P_t^{FLAT}+AI_t}$$
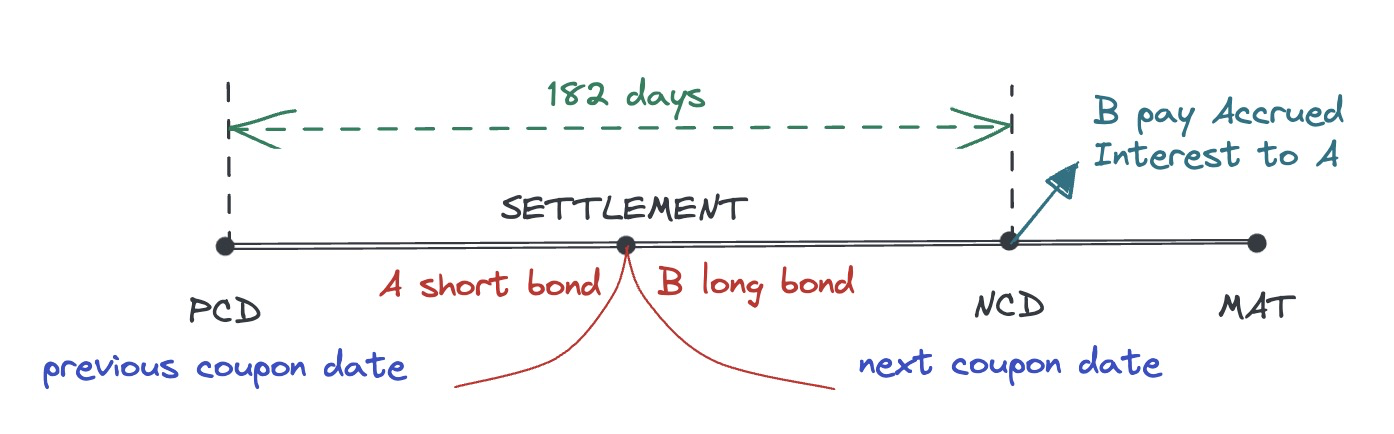
- $$\color{red}{P_t^{FULL}=P_t^{FLAT}+AI_t}$$
short government
- Short governments refer to T-bonds and T-notes with only one coupon remaining (to be paid at maturity).
- 还有最后一期到期的T-bond
- Let LCD denote the last coupon date, NCD the next coupon date, and SD the settlement date. SD falls between LCD and NCD.
- x = NCD - LCD
- z = NCD - SD
- then $$AI_t=\frac{C}{2}\times \frac{x-z}{z}$$
- Market convention for computing YTM of such a instrument is using simple interest:
- $$y=(\frac{100+C/2}{P_t}-1)\times \frac{2x}{z}$$
- $P_t$ is dirty price
- 思路:收益/价格,年化再日化,使用simple interest
General price-yield relationship
- $$\color{red}{P_t=\frac{100}{\left(1+\frac{y}{2}\right)^{N-1+\frac{Z}{X}}}+\frac{\frac{C}{2} \times \frac{Z}{X}}{\left(1+\frac{y}{2}\right)^{\frac{Z}{X}}}+\sum_{j=1}^{j=N-1} \frac{\frac{C}{2}}{\left(1+\frac{y}{2}\right)^{j+\frac{Z}{X}}}}$$
- 第一项:PV of par;第二项:part of coupon belong to buyer;第三项:PV of coupon
- N 是还有几次coupon剩余,X是NCD-LCD,Z是NCD-SD
- $P_t$ 是 dirty price
Yield to Maturity
- YTM, is the discount rate at which the present value of all future promised cash flows of a bond equals its price.
- Spot rates are general, as they are only related to time to maturity
- YTM is bond-specific!
- 不能用来给别的bond定价
- Assumptions embedded in YTM:
- All cash flows received during the lifetime of the bond are reinvested at the same YTM;
- The bond is held till its maturity.
- An important implication: spots rates are used for asset pricing, but YTMs are not!
Yield measures
- Bond equivalent yield
- $$BEY=periodic\times n$$
- for semiannual bond, n = 2
- Effictive annual yield
- $$EAY=(1+periodic)^n-1$$
- Current yield
- $$CY=\frac{\text{dollar interest}}{\text{market price}}$$
some relationships
- For par bond (price = par)
- coupon yield = current yield = YTM
- For discount bond (price < par)
- coupon yield < current yield < YTM
- For premium bond (price > par)
- coupon yield > current yield > YTM
YTM = coupon yield + capital gain yield
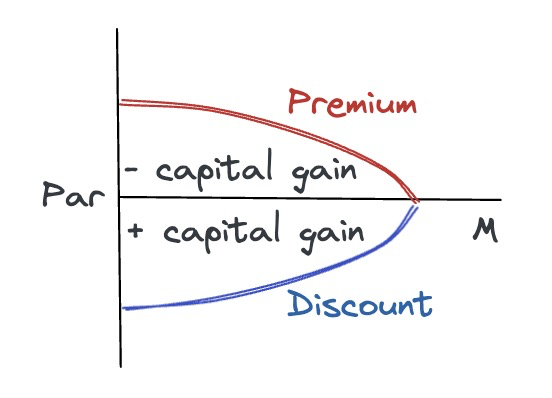
- YTM is not HPR (holding period return)
- 只有当hold the bond to maturity 才是
Term Structure and yield curves
- Term structure of interest rate refers to the relationship between spot rate and time to maturity, which is represented by spot rate curve.
- 利率期限结构
- 对于spot-rate
- Yield curve is the plot of yield to maturity against time to maturity or a risk measure (e.g., duration).
- Par yield curve is the yield curve for a group of bonds priced at par.
- Shapes: normal (upward), inverted (downward), humped
- Components: level, slope, curvature
- 对于不同的bond!
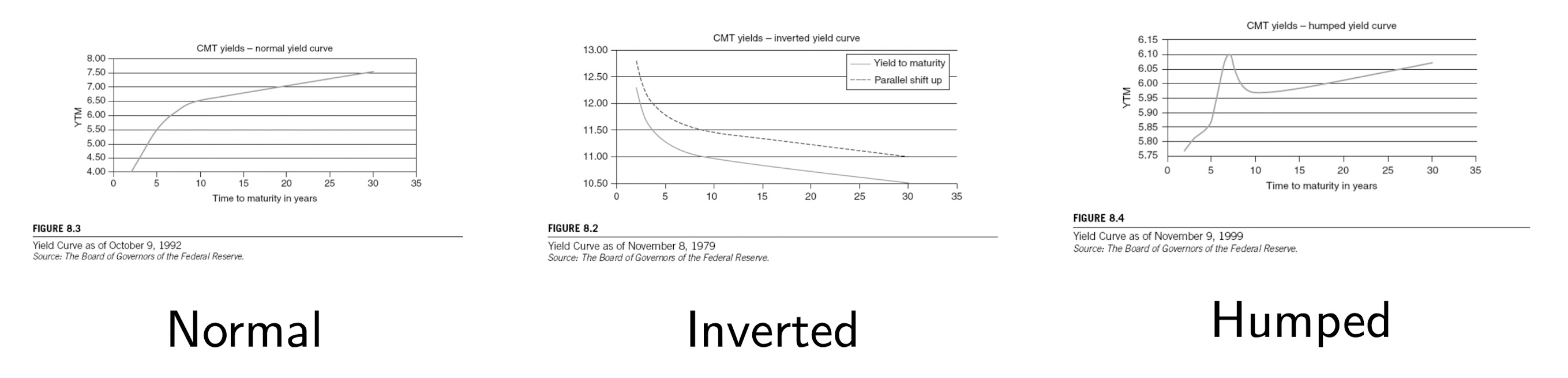
Hypothesis of yield curve
- Expectations theory: 期望理论
- the term structure reflects the market’s expectations of future interest rates.
- Preferred habitat theory: 优先偏好理论
- different bond investors prefer a particular maturity length over another, and they are only willing to buy bonds outside of their maturity preference if risk premia for other maturity ranges are available.
- Liquidity preference theory: 流动性偏好理论
- investors prefer cash or other highly liquid holdings, suggesting that an investor should demand a higher interest rate or premium on securities with long-term maturities that carry greater risk because, all other factors being equal.
- Market segmentation theory: 市场分割理论
- the market for each segment of bond maturities consists mainly of investors who have a preference for investing in securities with specific durations: short, intermediate, or long-term.
L3: Repo and monetary policy interest rate system
Repurchase Agreement
- Repurchase agreement (repo) is a contract under which the seller sells a security on the initiation date with an deal to repurchase it at a higher price on a specified later date.
- Repo is an important short-term financing tool in financial markets.
Conventional repo
Purpose of repo is to borrow money
- Initial transaction: X give treasury note to Y and get cash
- Closing transaction: X get teasury note back and give Y cash and interest
- used to borrow short-term money
- essentially a secured loan for X with the security as collateral
- X retains the cashflow rights
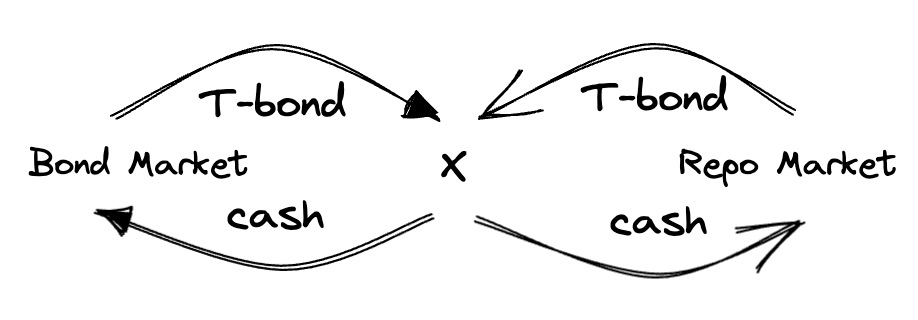
例子
- 6月10日,X买入T-bond,从Y那里借了值当前债券价格的99.5%(Y要保护自己from market and credit risks),Y take a haircut
- 6月13日,X卖出T-bond,将3天的accrued interest连同本金还给Y,自己赚剩下的钱
- interest rate 按照 simple interest 计算
- 由于长期金融工具的interest高,因此从short-term借钱去投long-term产品,可以赚钱
- riding the yield curve
- 这种操作面临的风险是interest rate risk和liquidity risk(债券可能卖不出去)
Reverse repo
Purpose of reverse repo is to borrow security using cash as collateral
- Initial transaction: X give cash to Y in order to get bonds
- Closing transaction: X give back bond to Y and get cash and accrued interest back
- a monetary policy tool, in order to inject liquidity to the market
repo specialness
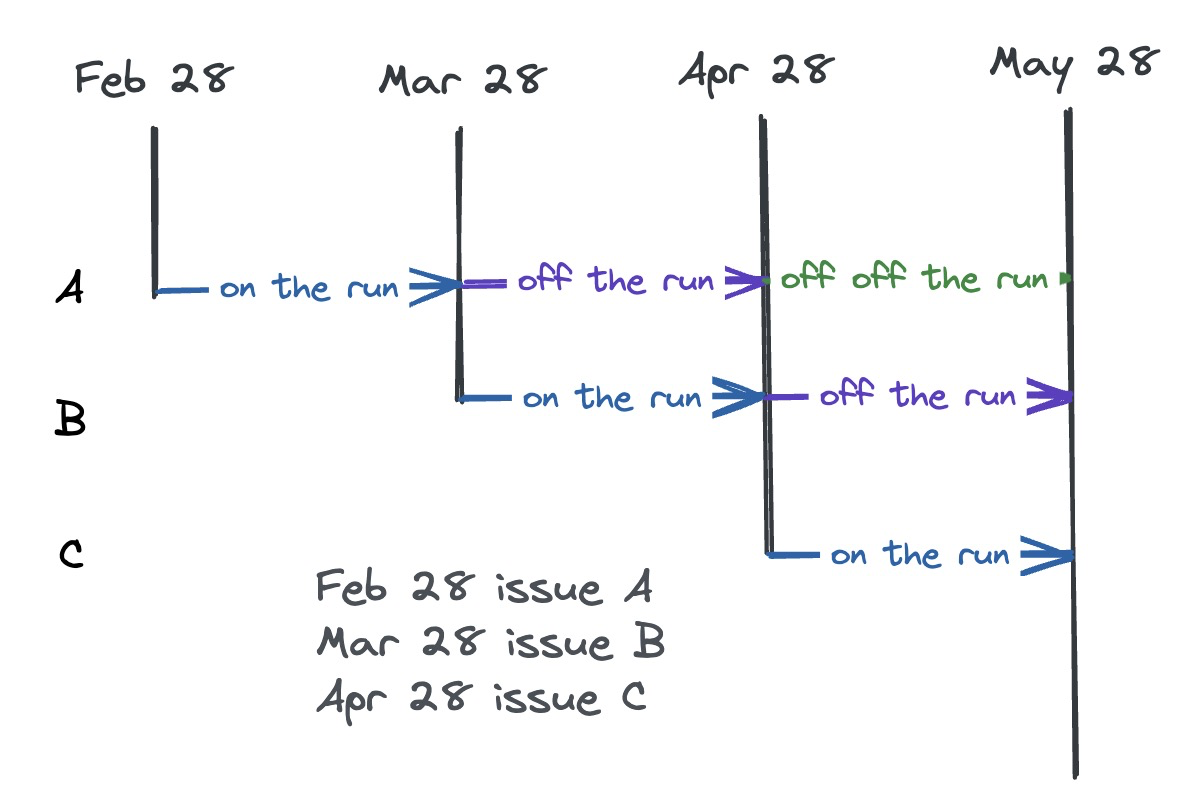
- Special (Collateral) repo: 只能还借走的那一个bond
- General (Collateral) repo: 一类债券都可以,比如只要是两年期 on the run 的T-note都可以用来还
- 通常来说,special repo rate 非常低,因为 I desperately need it.
- 交易策略: lend out special asset, use the cash to buy general asset.
Repos in China
两种repo形式
- Pledged repo 质押式
- a type of short-term financing business where bonds are used by both trading parties as a pledge of rights
- borrower 向 lender 借钱,约定按照未来确定日期的 specified repo rate 还钱
- 与 conventional repo 类似,但是在这种情况下 bonds 被冻结了,lender 不能动这些债券
- 造成了 treasury bond 流动性下降
- Outright repo 买断式
- positive repo party sells bonds to the reverse repo party, agreeing that the positive repo party buys from the reverse repo party an equal number of same-type bonds at a predefined price in the future.
- 会有交易成本
- 只占中国的百分之十左右
- 相当于把bond进行了交割,bond 产生的interest 归 reverse repo party
交易场所
- Interbank market
- 符合条件的银行与金融机构,无个人投资者
- 双边交易
- 11种maturities:1日,7日,14日,21日,1月,2月,3月,4月,6月,9月,1年
- 两种repo都在这里交易
- Exchanges (SSE,SZSE)
- 无商业银行
- 只有质押式回购
- 双边交易
- bond pledge-style agreement repo (customized)债券质押式协议回购;bond universal pledge-style repo(standardized)
- 三边交易
- 第三方用来提高交易效率,减小风险
Applications of reverse repo in open market operation
- Open market Operation, OMO, 指中央银行在公开市场上购买/售卖证券
- for liquidity injection 注入流动性
- PBOC purchases collateral eligible debt instruments from the interbank market participants and sells it back to the market seven days later
- As short-term policy rate
- PBOC lowered the interest rate on liquidity tool by 10 basis point to 2.15% from 2.25%, as it restarted its 14-day offerings for the first time since late January.
- Key maturities: 7day, 14day, 28day
- for liquidity injection 注入流动性
China’s policy rate system
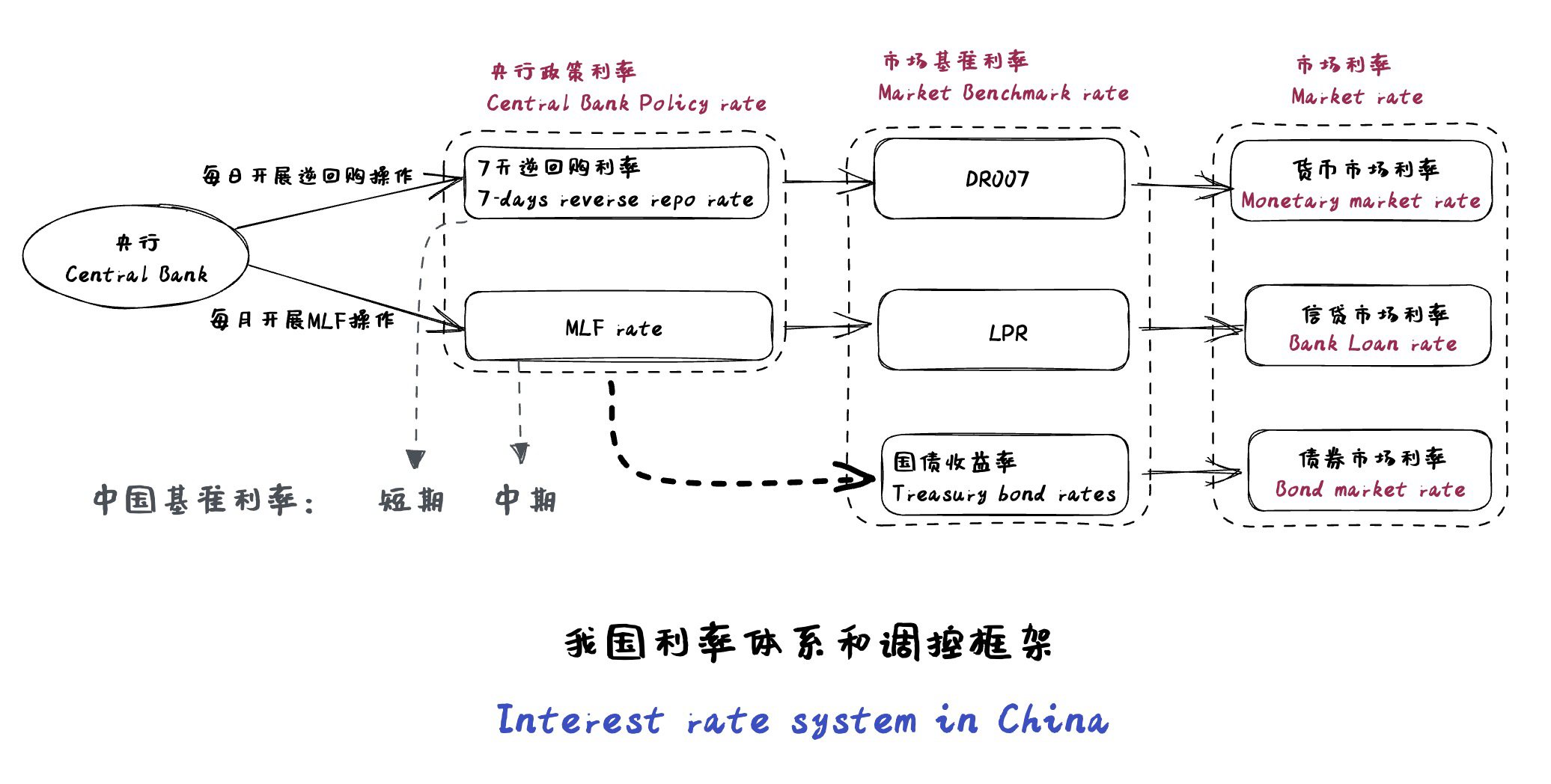
DR007
- 7 days repurchase (repo)rate for depository institutions
- short term market benchmark rate
MLF, Medium-term Lending Facility, 中期借贷利率
- lending facility that PBoC lends to financial institutions through scheduled (monthly) auctions
- Participants: policy and commercial banks
- high quality collateral, such Treasury bonds and central bank bills, are required
- Maturity: 3 months, 6 months, 1 year
- lending facility that PBoC lends to financial institutions through scheduled (monthly) auctions
Prime rate (best interest rate)
- 银行给信用高的用户的最佳借贷利率
Loan Prime rate, LPR
- quoted by 18 banks based on OMO operations rates (mainly MLF)
- calculated by National Interbank Funding Center 银行同业拆借中心
- benchmark for bank lending
- 每月20号上午9点15公布
Interest rate corridor
- the range within which the operating target of the monetary policy–a short-term interest rate – moves around the policy rate announced by the central bank
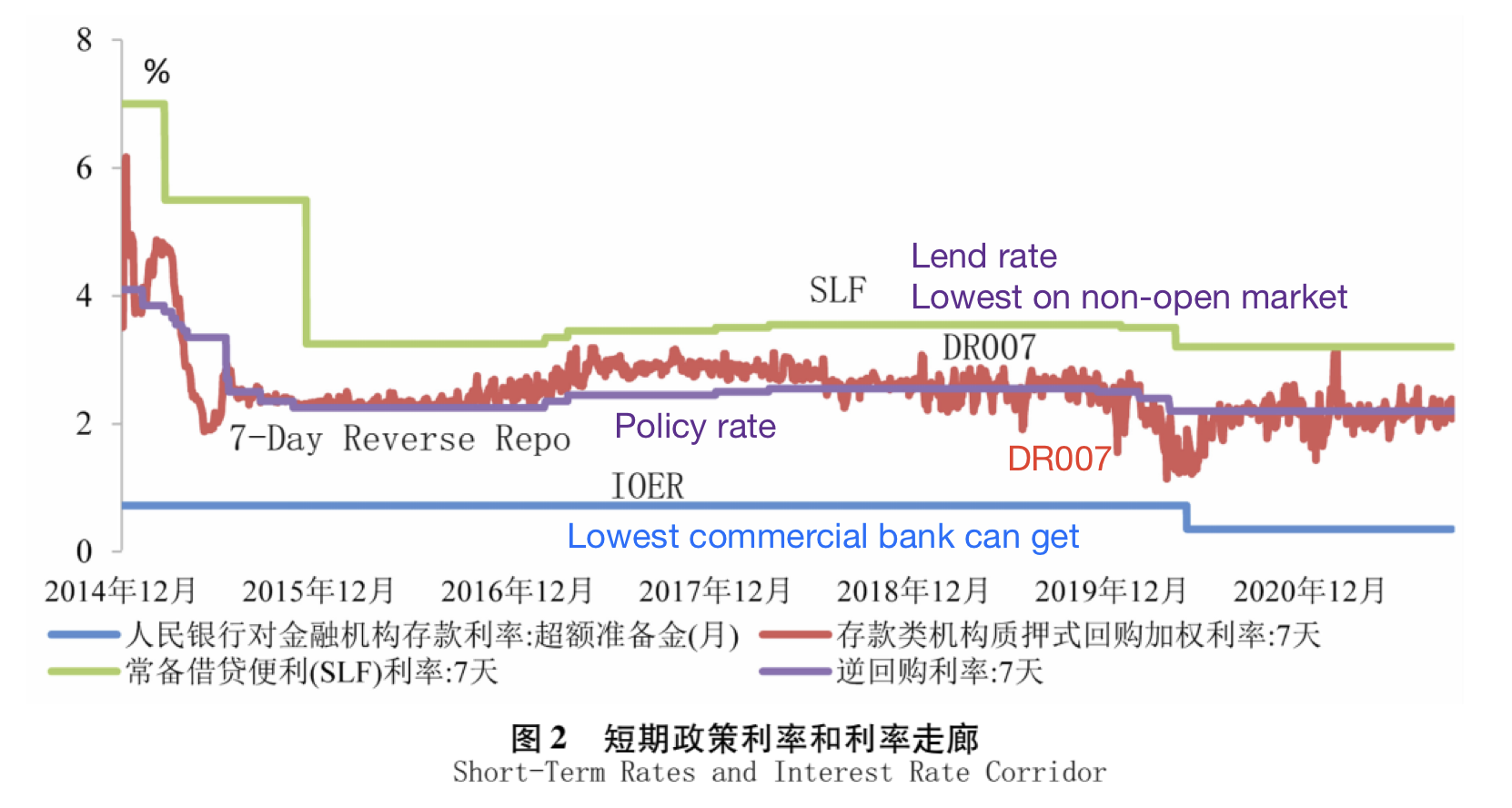
- the range within which the operating target of the monetary policy–a short-term interest rate – moves around the policy rate announced by the central bank
Standing lending facility, SLF
- lends on a bilateral and on-demand basis rather than in the open market through scheduled auctions
- 非公开市场
- 例如,商业银行找央行单独说,非常需要钱
- 通常出现了流动性的问题
- act as a last resort
- maturities: O/N (overnight), 7 day, 1 month
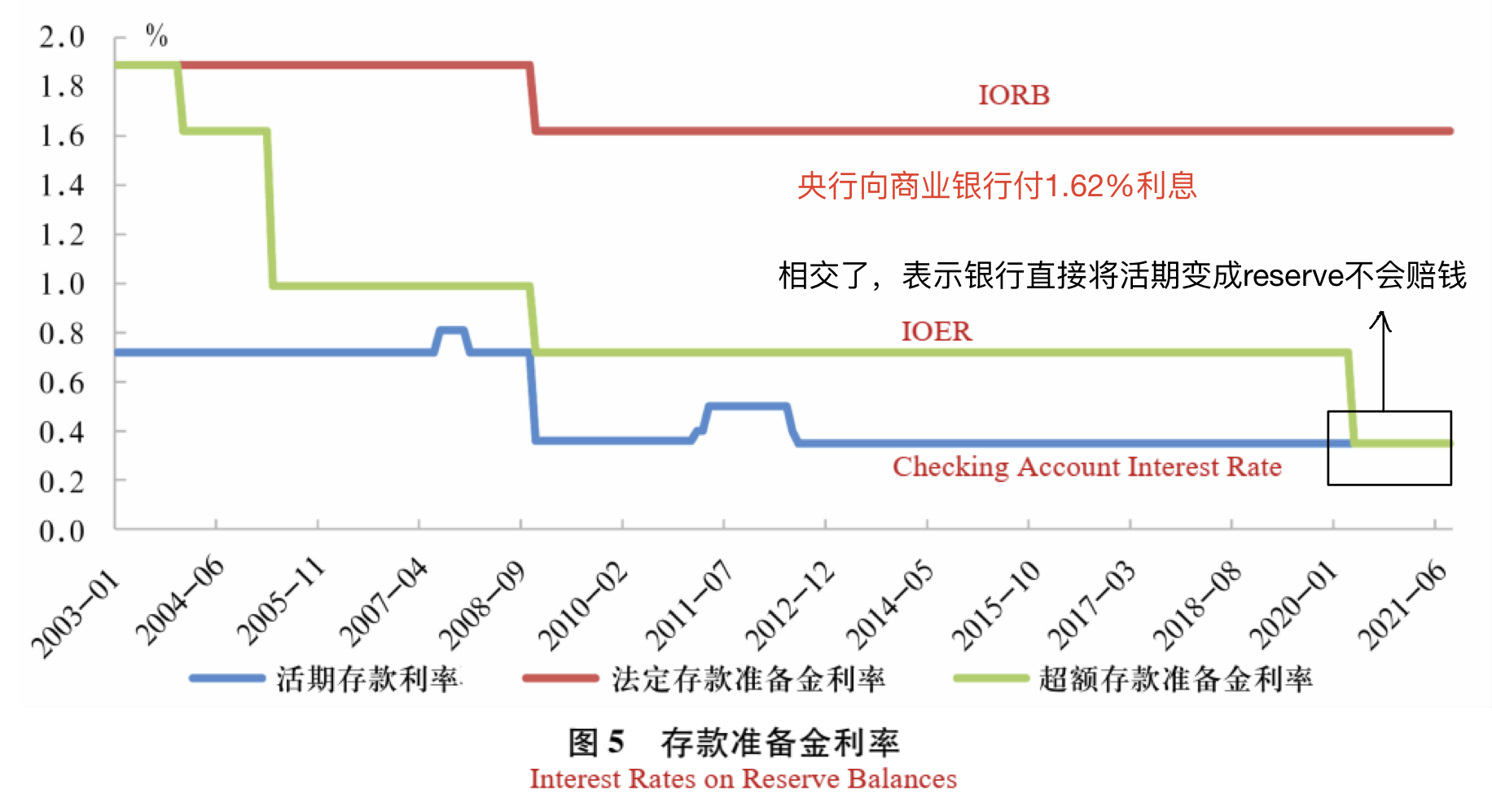
Interest rate on reserve balances(IORB)
- rate of interest that central bank pays on reserve balances maintained by depository institutions
- rate is set by central bank
- important monetary policy tool
- 例如:客户向我存款100元,商业银行向央行存11元(目前的要求是11%)
- 防止商业银行破产
Interest rate on excess reserve(IOER)
- 超过11%的部分存入央行的利率
- 也是货币政策工具
- 提高IOER给商业银行激励去把更多钱存到央行,减少了money supply
L4: Treasury Bond
Treasury bond market in China
Treasury bond
- In China, Treasury bond are the liabilities of the central government issued by the Ministry of Finance.
- considered risk-free
- 两种:
- book-entry Treasury bond 记账式
- 只issue给institution和很少一部分个人投资者
- 在二级市场可交易
- coupon-bearing bond的maturity都长于1年(最长50年)
- discount bond的maturity有 28, 63, 91, 182, 273 days
- savings treasury bond 储蓄式
- 电子或凭据形式,issue给个人投资者
- 不可交易
- maturity: 3 year, 5 year
- book-entry Treasury bond 记账式
Treasury bond market
- 一级市场
- tender offer (招标)记账式 to members of treasury bond underwriting syndicate
- issue 储蓄式 via underwriters
- issue targeted treasury bond to targeted social security instutitions and insurance companies (如社保基金)
- 少见
- 二级市场
- enchanges: SSE, SZSE
- OTC: interbank market and bank counter
member of underwriting syndicate
- 15个A级银行,40个B级银行/债券公司
- 每两年更新一次
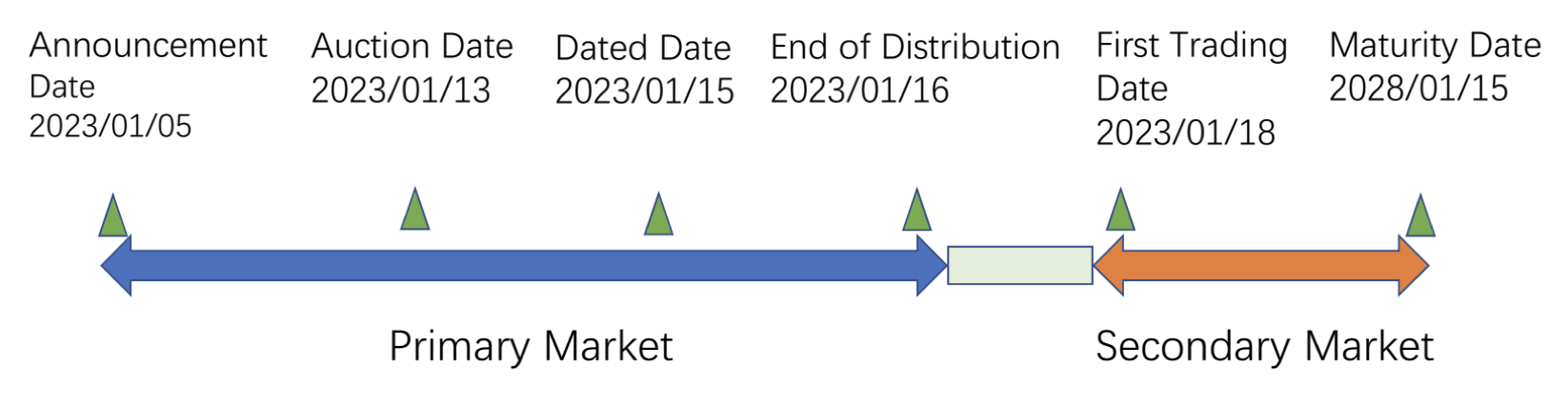
Issuance of Book-Entry Treasury Bonds
treasury tender offer
- 包括competitive 和 noncompetitive bids
- competitive同时报价价格与要求的数量
- noncompetitive只报价数量,作为price taker。也叫 additional bids
- noncompetitive bids通常只对A级银行允许,并且需要是10年期以下的coupon-bearing bonds
- quantity restrictions applied
- bid subject 是价格或利率
- 对于coupon-bearing bond,bid 利率
- 对于discount bond 和 reopening issue of coupon-bearing bond,bid价格
标位 bid positions 与 限制 bid restriction
Each issue notice stipulates the unit of change in bid position.
The unit tells the minimal difference in price/interest rate between two adjacent bid positions.
In an interest rate auction, the unit of change in the bid position is 1 basis point.
In a price auction, the unit of change in the bid position is stipulated in the notice.
- The unit typically increases with bond maturity;
- For example, 0.001 yuan for the 2023 28-day (20 billion yuan) and 63-day (20 billion yuan) discount bonds (Issues No.1 and No.2);
- For example, 0.002 yuan for the 2023 91-day (40 billion yuan) discount bonds (Issue No.4).
限制
- 最高最低价差不能超过要求
- too wild will be DQ
bidding and underwriting amount requirements
- maximum bidding amount: 35% of the auction(competitive bidding)amount for a Class-A memebr; 25% for class-B member
- minimum bidding amount: 4% for Class-A member, 1.5% for Class-B member.
- minimum underwriting amount: 1% for Class-A member, 0.2% for Class-B member.
determine winning bid
- 在满足条件的报价中,从最高价/最低利息开始直到市场出清或者所有报价都accounted for
- the lower interest, the better for MoF
- bid 一家银行在一段时间内可以多次提交
- 最高的winning interest rate 叫做 stop-out yield (SOY)
- 同时报价了winning interest rate,按照报价的数量按比例分配,round up to 0.01 billion yuan, 将余下的给到先报价的公司
Pricing mechanism
- Multiple price/discriminatory auctions(American Auction)
- Each winning bid receives the interest rate it expresses to receive.
- Uniform price auctions(Dutch Aution)
- All winning bids receive the same highest interest rate at which the market clears.
- 对于报价 < stop-out yield的,全部按照stop-out yield购买
- Modified multiple price auctions
- 首先对所有winning bids 按数量对报的利率进行加权,算出利率
- Winning bids for interest rates equal to or below the coupon rate pay the par price
- Encouagement to bid for lower
- 报价小于这个平均数的,按照100元购买,按照平均利率
- Winning bids for interest rates higher than the coupon rate pay discount prices, calculated with the interest rates expressed to receive, respectively.
- 按照平均利率作为coupon rate,按照自己报的利率作为利率,将bond折价。用这个价格购买bond,按照自己报价的利率
- interest rate更高的付更低的款
- 公平
注意,这里面报价的利率实际上是coupon rate
Secondary Market Market-Making Support Operation
- Ministry of Finance (MoF) uses buy-and-sell tools to support market-making in the interbank market.
- When market supply exceeds demand, MoF buys Treasury bonds from market makers, called the buy operation
- When demand exceeds supply, MoF sells Treasury bonds to market makers, called the sell operation
- Participating institutions are simultaneously Class-A members of the Treasury underwriting syndicate(15个) and market makers in the interbank market(11个).
US treasury securities
most important market in the world
Treasury financing
- Objective
- Fund the government at the least cost to the taxpayer over time
- Strategies
- Offer high quality products through regular and predictable issuance
- Promote a robust, broad, and diverse investor base
- Support market liquidity and market functioning
- Keep a prudent cash balance
- Maintain manageable rollovers and changes in interest expense
Classes of Treasury securities
- Marketable
- Can be traded in the secondary market
- Sold at auction, rates set via competitive bidding
- e.g., Bills, Notes, Bonds, TIPS, and FRNs
- Zero coupon bonds are created by market participants and are not issued directly by Treasury
- 是通过金融工具构造出来的
- Non-Marketable
- Can not be traded and can be sold only to Treasury
- Sold to investors by subscription, rates set administratively
- e.g., Savings Bonds, State and Local Government Series
Marketable Treasury securities
- Bills
- Maturities less than 1-year, sold at competitive auction at a discount to par.
- Returns par at maturity.
- Notes
- Maturities from 1-year to 10-years, sold at competitive auction, semi-annual coupon payments.
- Bonds
- Maturities > 10-years, sold at competitive auction, semi-annual coupon payments.
- Treasury Inflation-Protected Securities (TIPS)
- Maturities of 5-, 10- and 30-years.
- Sold at competitive auction. Semi-annual coupon payments.
- TIPS have a “Real Rate Coupon.” Principal is indexed to NSA-CPI(Non-Seasoned adjusted CPI)
- Floating Rate Notes (FRN)
- 2-year maturity. Sold at competitive auction.
- 每季度付利息,利率每周变化,按照13-week T-bill auction result
Treasury issuance calender
- 发行有一个pre-determined schedule
- 发行频率与maturity相关
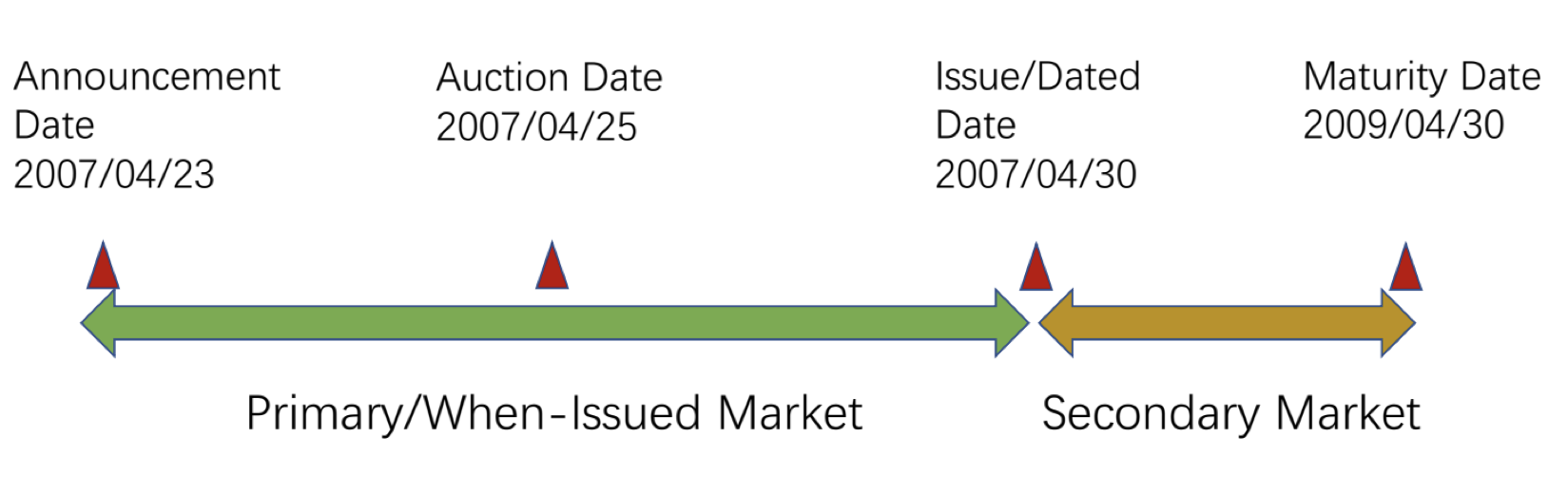
Treasury Auction
- 只有 primary dealer 拥有直接进行 auction 的权利
- pricing mechanism:uniform price auction
- 1999年从 American auction 改成了 Dutch auction
When-Issued trading
- When-issued (WI) is a transaction or trade in securities that are not yet issued, on the understanding that the trade will be settled once the securities are issued.
- When-issued trading occurs between the announcement date and the issue date.
- time concide with primary market
- Dealers and investors can take significant long or short positions that do not require financing.
- WI trading constitutes a special kind of forward market for non-existent securities.
- a special forward market
- Active WI markets exist for US Treasury securities and sometimes Freddie Mac securities issued by auction, e.g., reference bills.
Benefits of WI trading
- information discovery
- 对于 primary dealer,可以了解到客户希望的interest rate和quantity。并且由于签了contract,避免了非对称信息,必须进行交易。
Downside of WI
- Short squeeze
- squeezing the market means a dealer/market participant corners most or all available supply in security to engineer an artificial price rise;
- may refer specifically to the futures or repo markets when the supply of loanable or deliverable securities is reduced by such cornering activity.
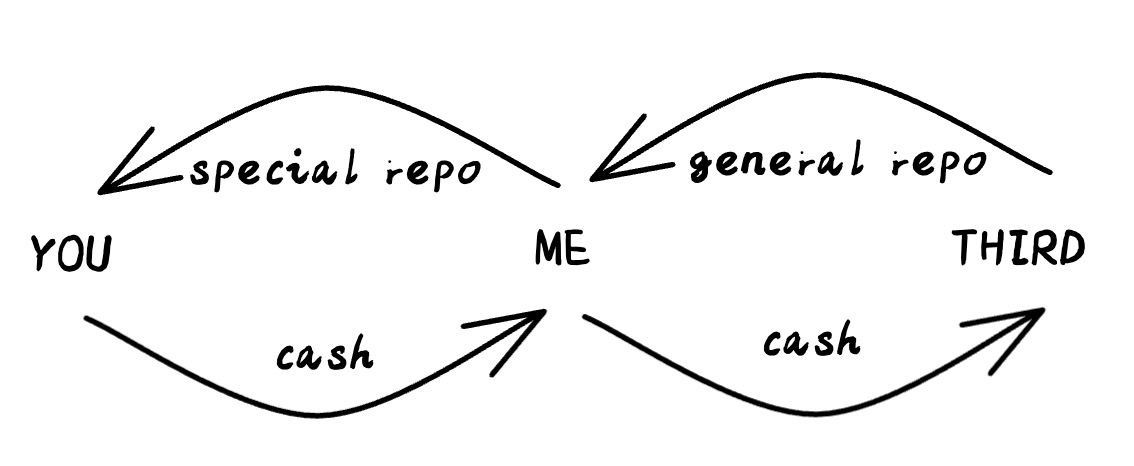
- Repo specialness
- refers to repo transactions in specific securities, where only the special securities can be delivered back to close out the transaction.
- substitution of similar collateral, such as other securities of the same issuer, are not accepted for transaction closure.
take advantages of the specialness
- Enter into a repo: sell your security and agree to repurchase it later.
- Since the security is scarce, you will obtain a high price relative to the “forward” price. That means you can borrow at a specially low repo rate.
- Invest the cash in a standard “non-special” investment and earn the difference between the prevailing market rate and the special repo rate.
- There exists an incentive to create such “specialness,” e.g., theSalomon Brothers scandal in 1991.
L5: Duration, PVBP, Convexity
- Interest rate risk refers to the adverse price movement of a bond resulting from the change in market interest rate. For bond investors, it is typically the risk that the interest rate will rise.
- inverse convex relationship between price and yield
- How to measure interest rate risk?
- Duration
- Convexity
Duration
Duration of a debt security is its discounted-cash-flow-weighted time to receipt of all promised cash flows divided by its price.
Consider a coupon bond price expressed in continuous compounding,$P=\sum_{i=1}^NC_ie^{-yt_i}$, duration is expressed as
- $$D=\frac{\sum_{i-1}^NC_ie^{-yt_i}\times t_i}{P}$$
Loosely speaking: average time to receive all the cash flows
$\color{red}{duration 没有单位!!}$
Duration is the price elasticity of interest rate, which measures a fixed income security’s exposure to interest rate risk.
$$\frac{\partial P}{\partial y}=-PD$$
thus,$$D=-\frac{\frac{\partial P}{P}}{\partial y}\approx -\frac{\frac{\Delta P}{P}}{\Delta y}$$
Definition
- Macaulay duration:
- $$D^{Macaulay}=-\frac{dP/P}{d(1+y)/(1+y)}=-\frac{dP/P}{dy}(1+y)$$
- 离散情况
- modified duration
- $$MD=-\frac{dP/P}{dy}$$
- 连续情况
Properties of duration
- A zero-coupon bond’s duration equals its maturity, implying that the zero-coupon bond is the most interest-rate-elastic instrument for a given maturity.
- A coupon bond’s duration is less than its maturity.
- Duration increases with maturity.
- Duration decreases with coupon rate and yield to maturity.
- Duration is time-varying.
- As a linear approximation of the price-yield relationship, duration may not work well for significant shifts in the term structure.
- Duration works only for parallel shifts in the term structure and may fail miserably if the term structure tilts while shifting parallelly.
PVBP
PVBP=PBP=DV01
The price value of a basis point (PVBP) or dollar value of 01 (DV01) is the change in a bond’s price due to a change in the interest rate.
PVBP is typically expressed as the change in value of a 1 million USD (par value) position in reaction to a change in the yield of one basis point, that is, $\frac{1}{100}$% .
是dollar measure
$\partial P/\partial y$ tells us how much a bond price will change when y increases by one, that is, 10,000 basis points.
$$\Delta_P=\frac{\partial P}{\partial y}\Delta_y=\frac{\partial P}{\partial y}\frac{1}{10000}$$
$$PVBP=\Delta_P\times 10000=DP$$
Trading and Hedging strategy
Hedging interest rate risk with Treasury futures contract
- Example
- Suppose we have a portfolio whose market value (P) is 7,500,000 USD. We would like to use Treasury Futures contracts to hedge the interest rate risk. The face value of one Treasury futures contract is 100,000 USD, and its price is 96 USD. The durations of the portfolio and Treasury futures contract ( $D_P$ and $D_F$ ) are 6 and 5, respectively. How many Treasury futures contract (N) should we trade?
- the objective function: 久期加权为0
- $$D_P+D_F\times F_C\times N=0$$
- solve for this equation, N = -94
- We should short 94 such treasury futures contracts.
Treasury futures
- A special kind of forward contract
- buy treasury-futures is equivalent to holding the bond, which means I will take on the risk.
- In the contrary, short the T-futures will get rid of the interest risk.
- 因为约定了远期之后,在这期间相当于我拥有bond,获得bond的coupon,获得了risk。
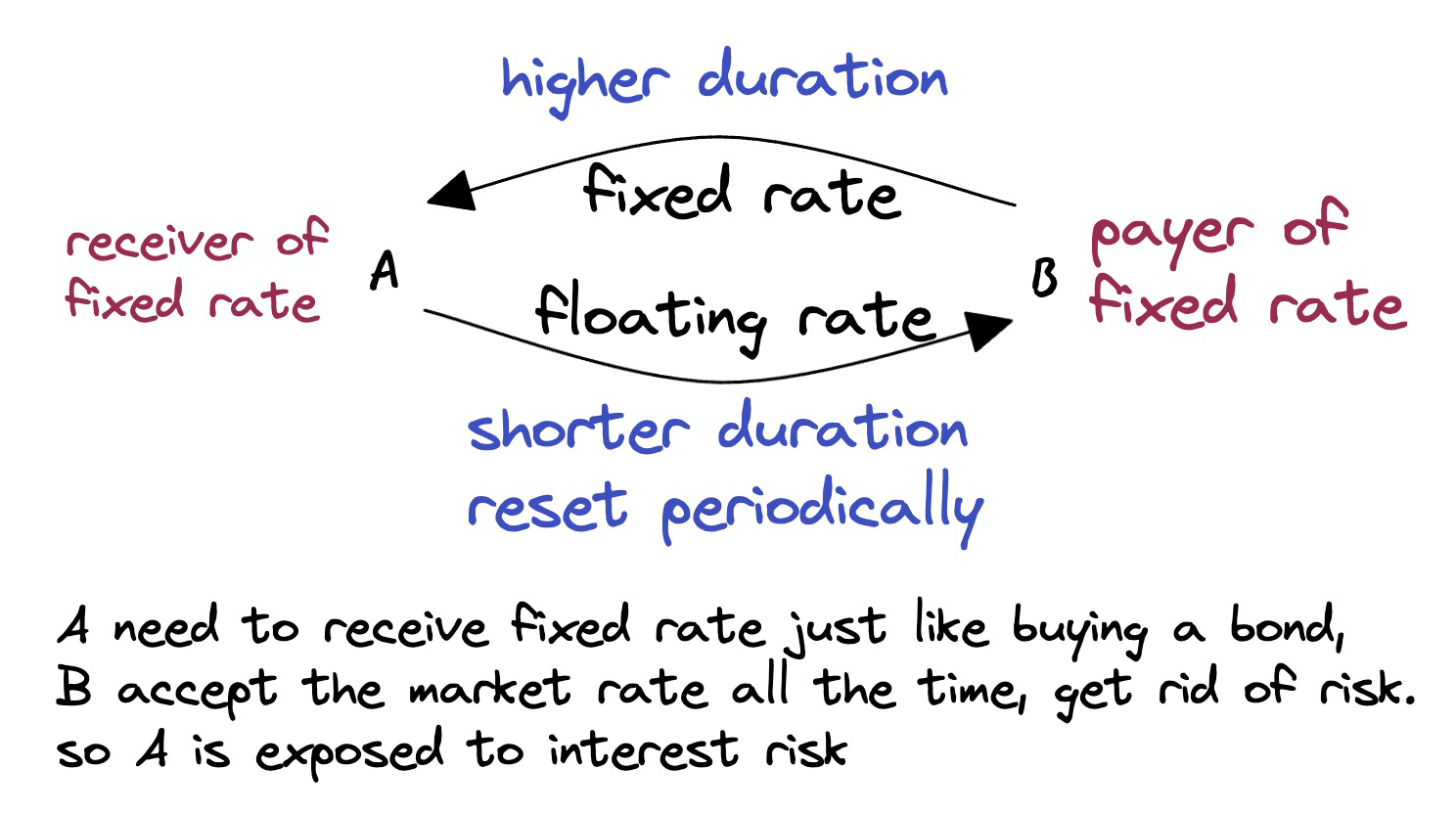
Hedging interest rate risk with interest rate swap
- Example
- A firm holds bonds of 100,000,000 USD (market value, A), whose duration ( $D_A$ ) is 5. At the same time, the firm owes a debt (L) of 90,000,000 USD, whose duration ( $D_L$ ) is 3. The firm wants to hedge its interest rate risk using interest rate swap. The notional principal of an interest rate swap contract is 100,000 USD, and the durations of its fixed-rate leg and floating-rate leg are ( $D_{FX}$ and $D_{FL}$ ) 4.5 and 0.6, respectively. How many interest rate swap contracts the firm should enter into (K)?
- the objective function: duration neutral
- $$[D_A\times A-D_L\times L]+[(D_{FX}-D_{FL})\times K]=0$$
- solve for the equation, K = -575
- firm should enter into 575 contracts, paying fixed rate and receive floating rate.
- Less costly than trading a bond
Spread Trading
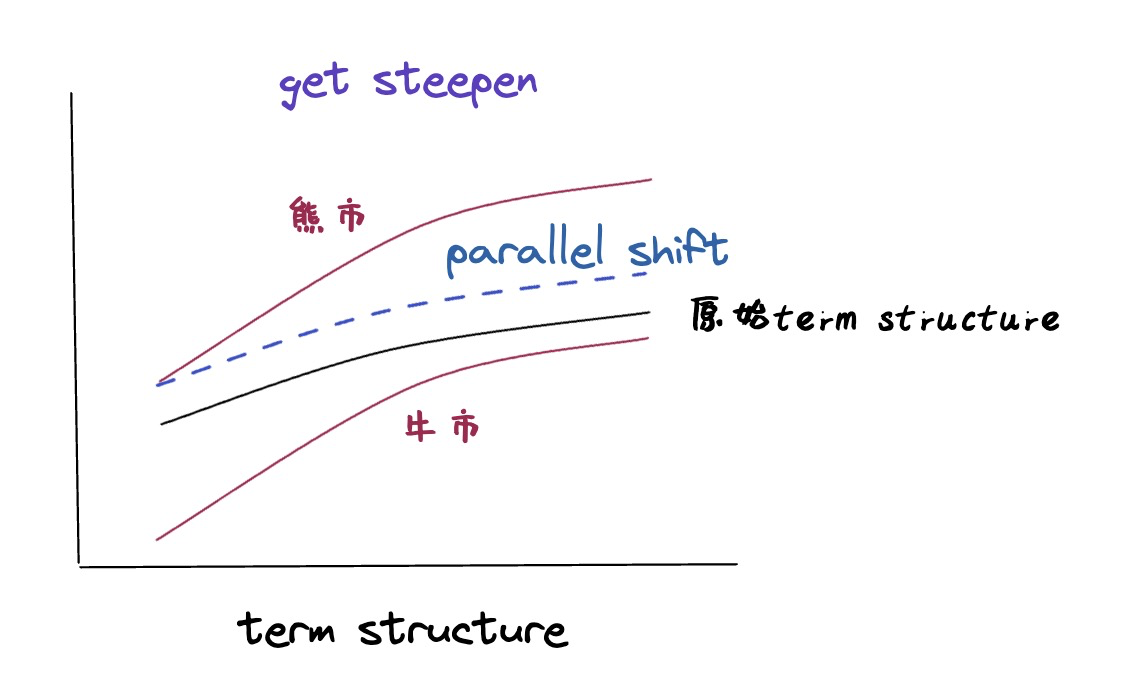
- Spread trading bets on changing slope of the term structure.
- We construct a trading strategy that pays off if the yield curve steepens or flattens sufficiently but is insensitive to parallel shifts in the term structure.
- There are two scenarios where the yield curve can steepen:
- short rates increase less than long rates (in a bearish market)熊市
- short rates fall more than long rates (in a bullish market)牛市
- To gain exposure to the yield curve slope, we need to trade (at least)two bonds of different maturities.
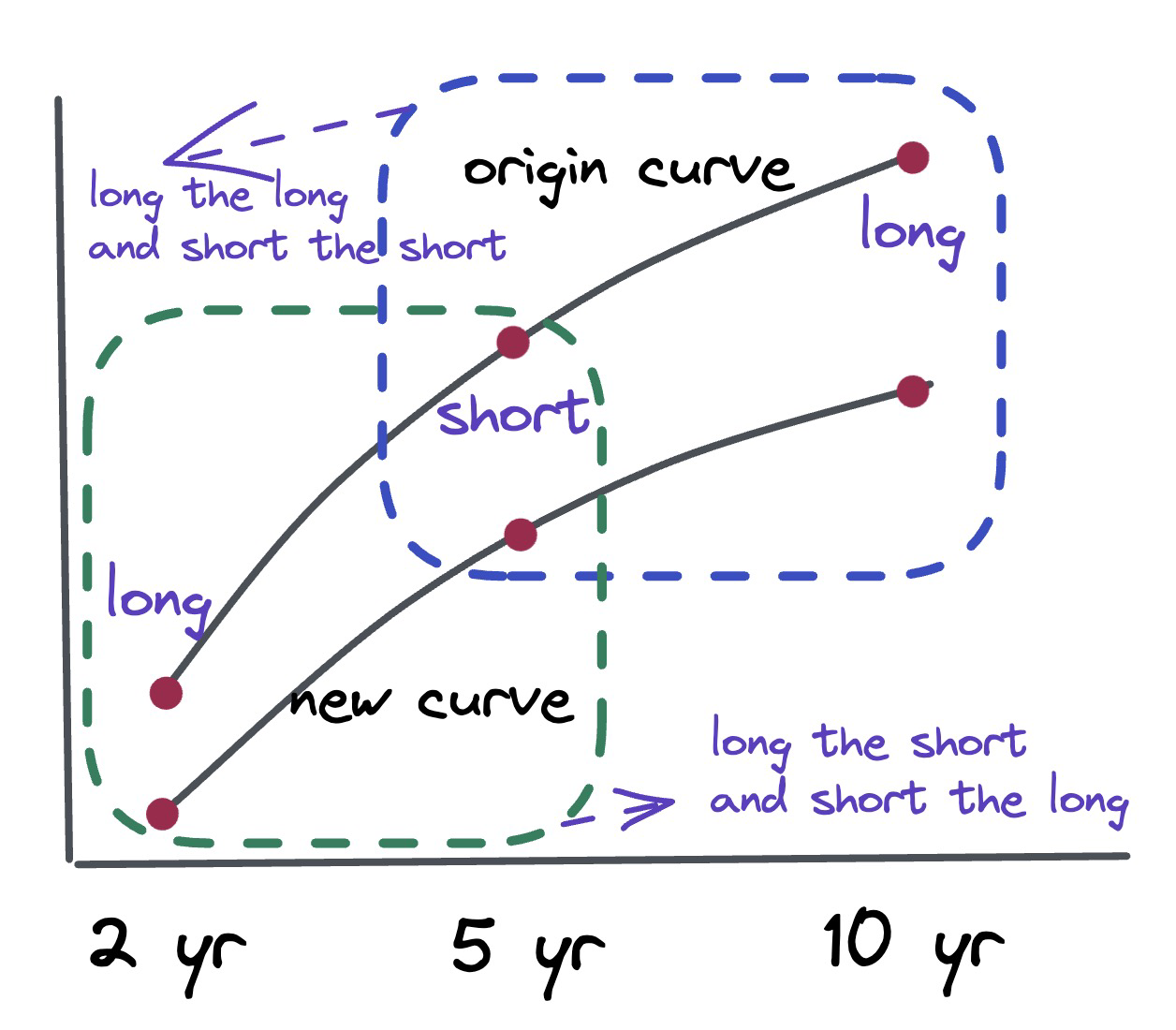
- Short the long bond and long the short bond
Example
- Positions: short a 6-year bond with 8% coupon and long a 2-year bond with 5% coupon
- Suppose the current term structure is flat at 5%, we compute
- $$B_{short}=99.76 \quad B_{long}=114.52\quad D_{short}=1.95 \quad D_{long}=5.07$$
- Suppose we long 100 short bonds; how many long bonds do we need to short in establishing duration neutrality?
- $$\frac{n_{\text {short }} B_{\text {short }}}{n_{\text {short }} B_{\text {short }}+n_{\text {long }} B_{\text {long }}} D_{\text {short }}+\frac{n_{\text {long }} B_{\text {long }}}{n_{\text {short }} B_{\text {short }}+n_{\text {long }} B_{\text {long }}} D_{\text {long }}=0$$
- The result shows that we need to short 33.57 long bonds.
- This duration-neutral portfolio is worth $6,132, and its value will increase if the yield curve slope rises substantially.
实际中
- long the short and short the long
- 买入短期,卖空长期
- 通常需要repo/ reverse repo
- The position will be neutral to parallel shifts in the yield curve, that is, duration-neutral
- $$n_{short}\times PVBP_{short}=n_{long}\times PVBP_{long}$$
- 实际情况中,即使确实存在spread,这种交易也不怎么挣钱
- 主要原因是bid-ask spread !!!
- 其他可能因素:haircut,special repo rate,repo rate
Convexity
Convexity is the change in the slope of the price-yield curve for a slight change in the yield.
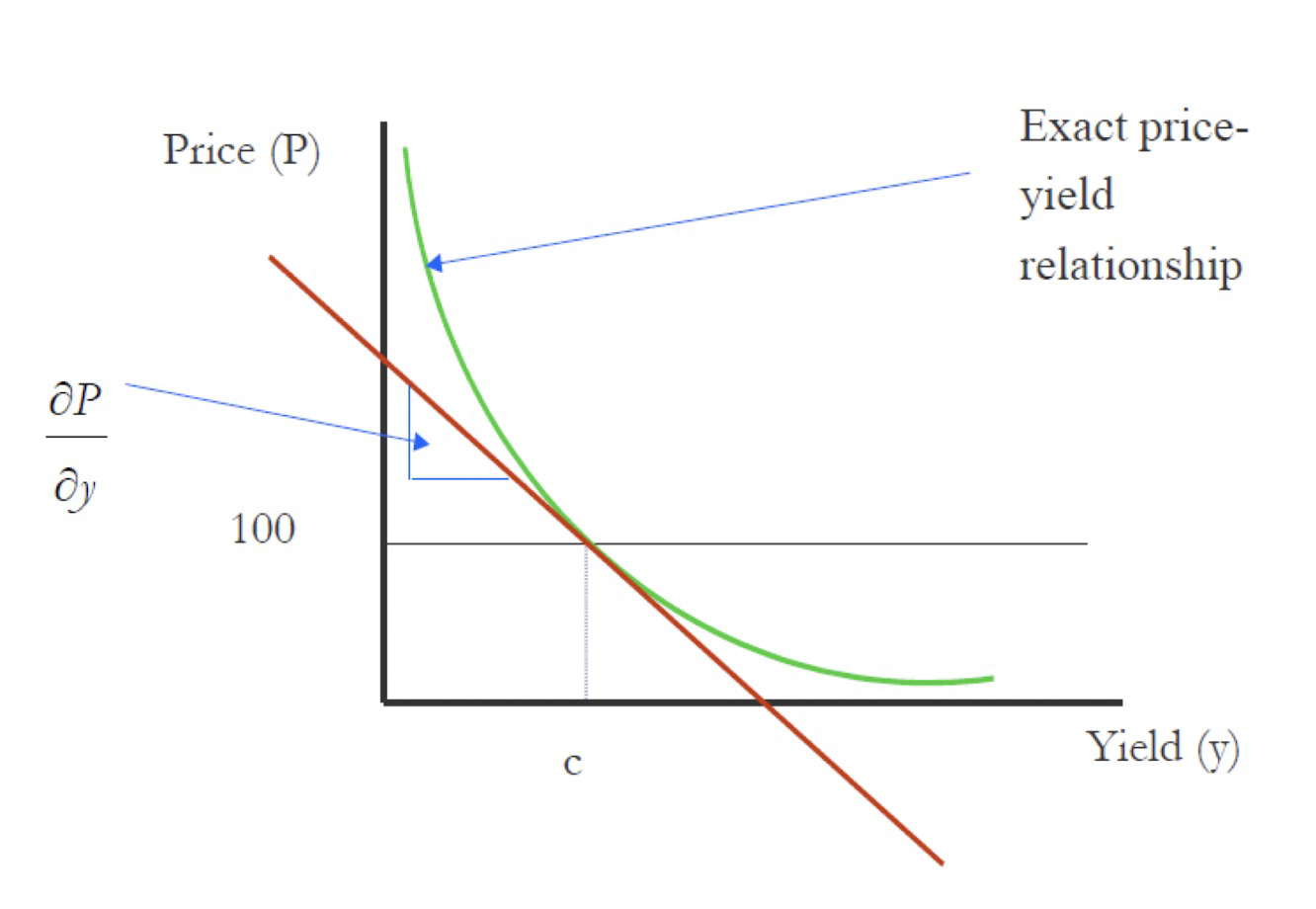
A bond’s convexity is measured as the second derivative of the bonds price to its yield
- 泰勒展开
- $$\color{red}{dP=\frac{\partial P}{\partial y}dy + \frac{\partial^2P}{2\partial y^2}(dy)^2}$$
- 第一项系数是PVBP,后项系数 $\frac{\partial^2P}{\partial y^2}$ 是dollar convexity.
- 两边同除P
- $$\color{red}{\frac{dP}{P}=\frac{\frac{\partial P}{P}}{\partial y}dy + \frac{\frac{\partial^2P}{\partial y^2}}{2P}(dy)^2}$$
- 第一项系数是Duration,后项系数$\frac{\frac{\partial^2P}{\partial y^2}}{P}$ 是relative convexity.
- relative convexity 不是 duration 的导数
Dollar Convexity is
- $$$Conv=\frac{\partial^2P}{\partial y^2}=\sum_{i=1}^NC_ie^{-yt_i}(t_i)^2$$
Relative Convexity is
- $$RConv=\frac{$Conv}{P}=\frac{\frac{\partial^2P}{\partial y^2}}{P}$$
- 对于zero coupon bond, relative convexity = $t^2$
- 把前面的系数消掉了
Positive and negative convexity
Security exhibits positive convexity when its price rises more due to a downward movement in yield than its price falling due to an equal upward movement in yield.
Bullet securities typically exhibit positive convexity.
Callable bonds usually exhibit negative convexity at lower yields. The price of a callable bond might drop as the likelihood that the bond will be called increases, and the shape of a callable bond’s curve of price to yield is concave or negatively convex.
- $$P_{callable}=P_{regular}-V_{\text{call option}}$$
- 当利率下降时,等式右边两项同时上升,要看两者的上升速度与绝对值
- 当上升绝对值V更高时,会出现concave
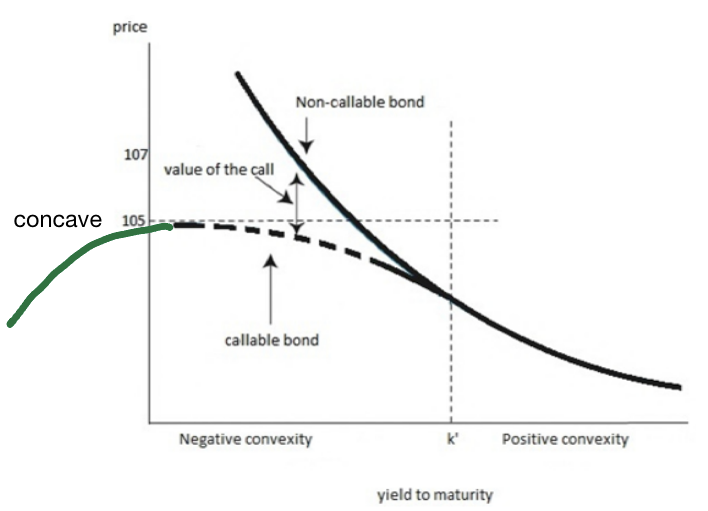
Most mortgage securities exhibit negative convexity due to the mortgage borrower’s incentive to refinance at a lower rate when market yields decline.
- 与callable bond很像
Property of Convexity
Positive convexity is desirable! Convexity bias explains the curvature of the yield curve.
- 由于convexity是二阶导的系数,当convexity是正的时候这一项永远是正的,因此 dP 会是正的,这是好事
- 考虑term structure,zero coupon bond 的 convexity 是 $t^2$, 当t增大时convexity增大,由于convexity是好事,所以人们愿意花更多的钱去购买这个bond(随着时间增大),因此bond的interest rate就会越来越低,造成向下的曲率
Bonds with greater convexity tend to gain more in price when yields fall than they lose when yields rise.
The more convex a bond price is, the more valuable the bond is.
If interest rates are volatile, this asymmetric response of price to yield is more desirable.
Butterfly trade
A trading strategy to take advantage of convexity by establishing a duration-neutral trade.
- 构造一个零久期的组合,但 relative convexity 是正的,相当于在relative convexity的公式里面把第一项对冲掉了,永远是正的。
对于三个久期的bond,short中间的,long长的和短的。

实际上是在trading flattening
- 可以把这个 butterfly trading 看成两个 spread trading 的组合,前一个是long the short and short the long,后一个是 short the short and long the long
- 如果变的flatten,后面的组合会挣钱,前面的会赔钱,但由于curve,后面挣得更多
- 变的更steapen时,相反。
- 因此本质上是在赌term structure 的变化趋势。
- 如果term sturcture 变成一个开口向下的二次函数型,在两侧都可以盈利。
convexity 本身数值的变化(曲率不变)不会有多少利润。
L6: Term structure and Yield Curve
- Term structure of interest rates refers to the relationship between the yield to maturity of default-free zero-coupon securities and their maturities.
- Yield curve is the plot of yield to maturity against time-to-maturity or a risk measure (e.g., duration).
Constructing the Term structure
- 如何构造term structure?
- 第一步,bootstraping;第二步,interpolation
- 现实中:
- 第一步:看到的所有bond的 YTM 看成是par yield,画一条线 interpolation
- 市场的平均
- 第二步:从第一步的线中提取 bootstraping 需要的点
- 例如,Maturity= 0.25, 0.5, 1, …
- 第三步:interpolation
- 第一步:看到的所有bond的 YTM 看成是par yield,画一条线 interpolation
Bootstraping
自举法
a self-starting process that is supposed to proceed without external inputs.
即,根据市场上可观测到的数据直接计算出来 yield。
- 使用连续复利公式
- $$PV=FV*e^{-rt}$$
对于maturity小于1年的直接计算yield(没有coupon paying 的 bond)
对于有coupon的bond,根据每次付息时的term structure计算maturity的term sturcture
- 例如1.5年期债券,半年付息,假定根据观测数据已知 $y_{0.5}$ 和 $y_1$, 由此计算 $y_{1.5}$
Par yield means the yield of a bond trading at the par
有了spot rate 就可以计算 forward rate
- 对于连续复利,forward rate的公式是:
- $$f_{t_1,t_2}=\frac{s_{t_2}\times t_2-s_{t_1}\times t_1}{(t_2-t_1)}$$
Interpolation
- Interpolation is a statistical method by which known values are used to estimate unknown values. Fitting the yield curve means estimating the yields for unobserved maturities.
- 把离散的点连起来
- Linear interpolation
- 非常不好,不要用
- Non-linear methods
- Nelson-Siegel and its variant Nelson-Seigel-Svensson are leading parametric models
- Pros: fewer parameters; easier to implement (by treating the term structure as a whole)
- Cons: less precise
- Splines-based models
- Pros: precise fits (by cutting the term structure into pieces)
- Cons: a large number of parameters to estimate
- Nelson-Siegel and its variant Nelson-Seigel-Svensson are leading parametric models
Nelson-Siegel model
Formula:
$$R(0, T)=\beta_0+\beta_1(\frac{1-e^{-\frac{T}{\tau_1}}}{\frac{T}{\tau_1}})+\beta_2(\frac{1-e^{-\frac{T}{\tau_1}}}{\frac{T}{\tau_1}}-e^{-\frac{T}{\tau_1}})$$
where $R(0,T)$ denotes the spot rate;
$β_0$ $β_1$ $β_2$ and $τ_1$ are constant parameters;
- $β_0$ is the level component—the long term rate (sometimes not estimated but pinned to a long rate, e.g., the 30-year spot rate).
- $\beta_1$ is the slope component—-downward ($β_1$ > 0) or upward ($β_1$ < 0)
- $\beta_2$ is the curvature component—a hump ($β_2$ > 0) or a trough ($β_2$ < 0).
- $τ_1$ is the shape parameter, determining the steepness of the slope and the location of the peak of the hump.
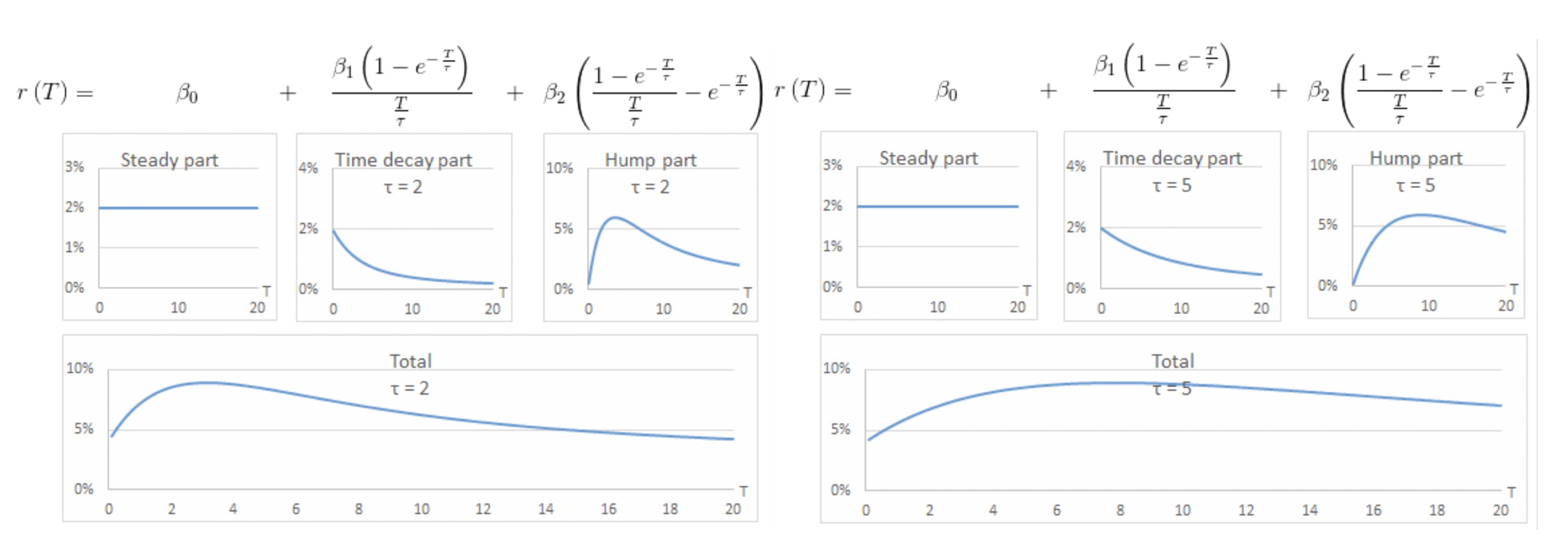
T is the time to maturity in annual units.
计算:
- $r(0,T)$ 表示从bootstraping得到的点, $R(0,T)$ 表示随机给参数赋初值后计算得到的点。
- $$\min_{\beta_0,\beta_1,\beta_2,\tau_1}\sum_{i=1}^N[r(0, T)-R(0, T)]^2$$
- 解这个方程,得到新的四个参数,就是要求的公式。
Nelson-Siegel-Svensson model
- Svensson 1994 extends the Nelson-Siegel formula adding a “second hump” with two more parameters $\beta_3$ and $\tau_2$ to allow for greater flexibility
- $$\begin{aligned}
R(0, T)= & \beta_0+\beta_1(\frac{1-e^{-\frac{T}{\tau_1}}}{\frac{T}{\tau_1}})+\beta_2(\frac{1-e^{-\frac{T}{\tau_1}}}{\frac{T}{\tau_1}}-e^{-\frac{T}{\tau_1}}) +\beta_3(\frac{1-e^{-\frac{T}{\tau_2}}}{\frac{T}{\tau_2}}-e^{-\frac{T}{\tau_2}})
\end{aligned}$$ - Central banks in the European Union widely adopt the Nelson-Seigel-Svensson model.
Polynomial Splines
- Spline originally meant a thin wood or metal slat in East Anglian dialect. By 1895, it had come to mean a flexible ruler used to draw curves.
- In mathematics, a spline is a numeric function that is piecewise-defined by polynomial functions. It possesses a high degree of smoothness at the places where the polynomial pieces connect, known as knots.
- We use Quadratic Splines for illustration, though Cubic Splines are more often used.
- $$B(0, t)= \begin{cases}B_0(t)=d_0+c_0 t+b_0 t^2 & t \in[0,1] \\ B_1(t)=d_1+c_1 t+b_1 t^2 & t \in[1,5] \\ B_2(t)=d_2+c_2 t+b_2 t^2 & t \in[5,7]\end{cases}$$
- 同样是最小化最小二乘,使用 solver 求解
Hermite Splines
在polynomial splines 基础上增加条件:
- 在 knots 点处,一阶导数也要相等
Central banks in the US, Japanese, British, Canadian, Chinese widely adopt the Splines-based model.
- 10 年前中国还用 NS model,现在用 splines-based model
Understand the yield curve
- Spot rate is the discount rate of a single future cash flow such as a zero-coupon bond:
- $$P_n=\frac{100}{(1+s_n)^n}$$
- Forward rate is the interest rate for a loan between two future dates contracted today:
- $$(1+s_n)^n=(1+f_{0,1})(1+f_{1,2})(1+f_{2,3}) \ldots(1+f_{n-1, n})$$
- 从这个式子来看,spot rate 可以看成是 forward rate 的一个 weighted average
- Generally, we have
- $$(1+f_{m, n})^{n-m}=\frac{(1+s_n)^n}{(1+s_m)^m}$$
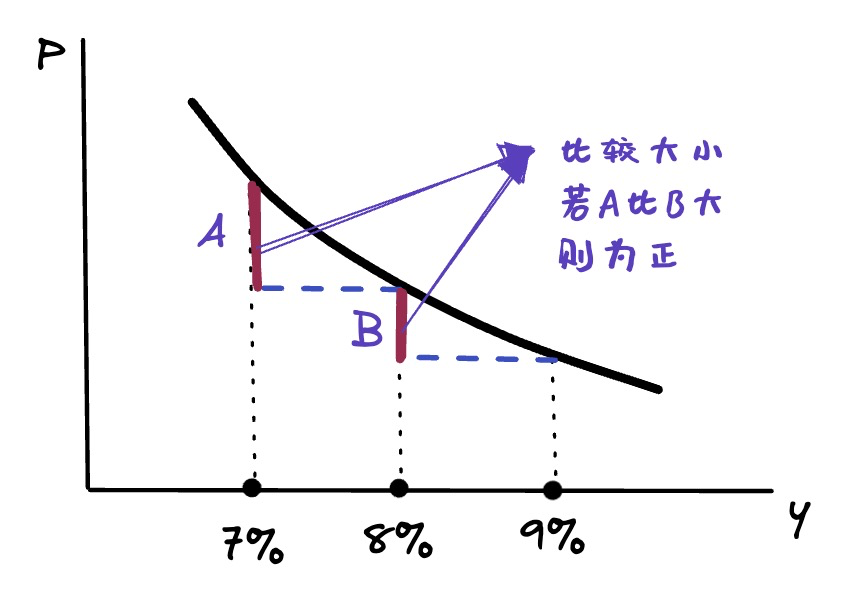
implied spot rates one year forward
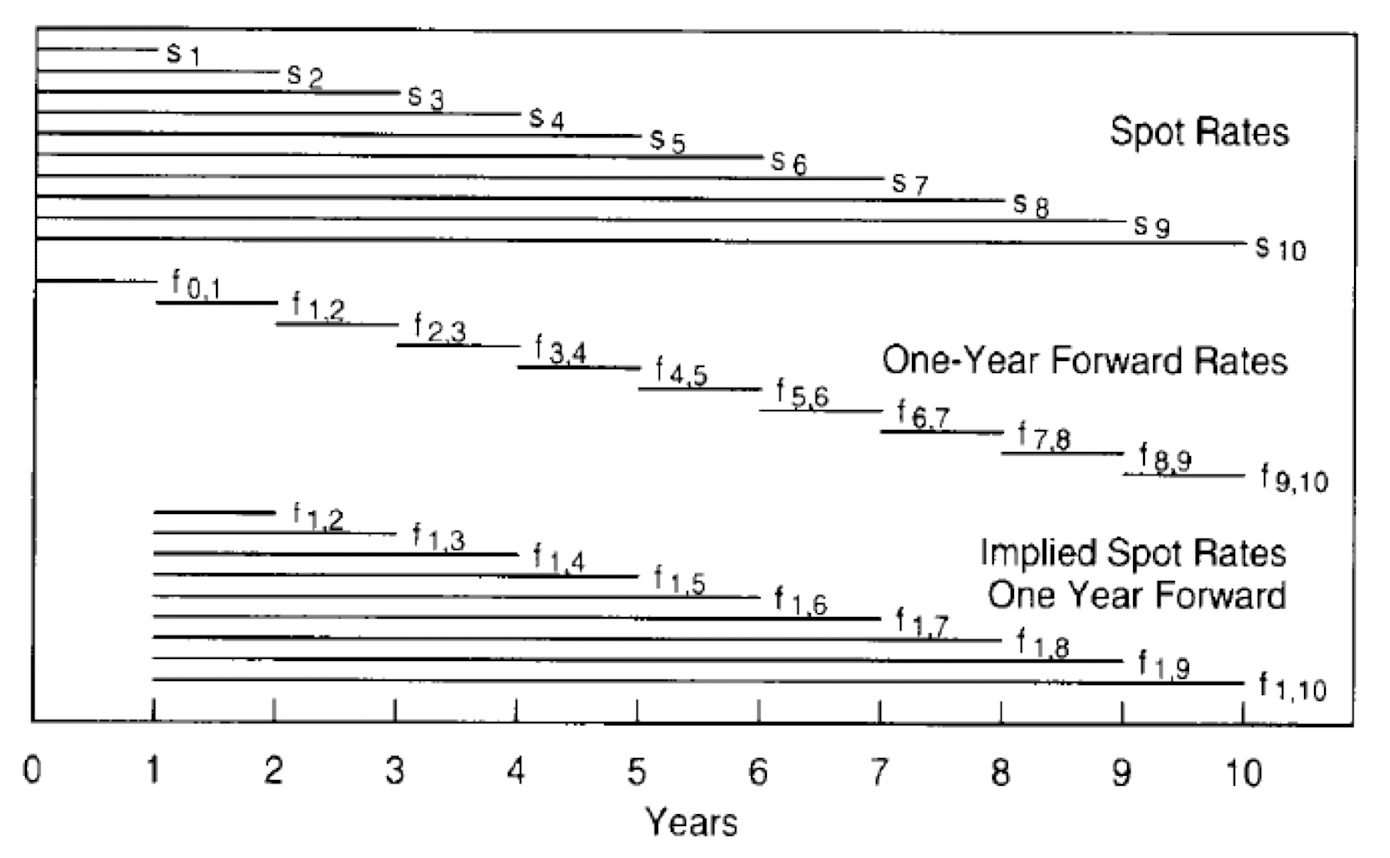
- 隐含的一年后的spot rate
- 只通过current spot rate就能推出来
- 如果 implied spot rates one year forward 全部实现,那么对于所有的 government bond,在 year 1的 holding period return 都一样
- $$\frac{(1+s_n)^n}{(1+f_{1,n})^{n-1}}=1+s_1$$
- 不管它本来的 maturity 是多少
- The forwards tell how much the yield of a longer-term bond needs to change to offset its initial yield advantage over the short-term rate.
- Alternatively, the forwards tell how much a given point on the spot curve has to shift to equate holding-period returns across bonds.
Implications,将bond yield分层
Pure Expectations Hypothesis (PEH)
- tells that any yield differences across bonds must imply future rate changes in expectation-implied spot rate one year forward is the result of aggregate expectations.
- Implication 1: all government bonds have the same near-term expected return $(S_1)$ regardless of their maturities.
- Implication 2: expected capital gains or losses offset the initial yield differences.
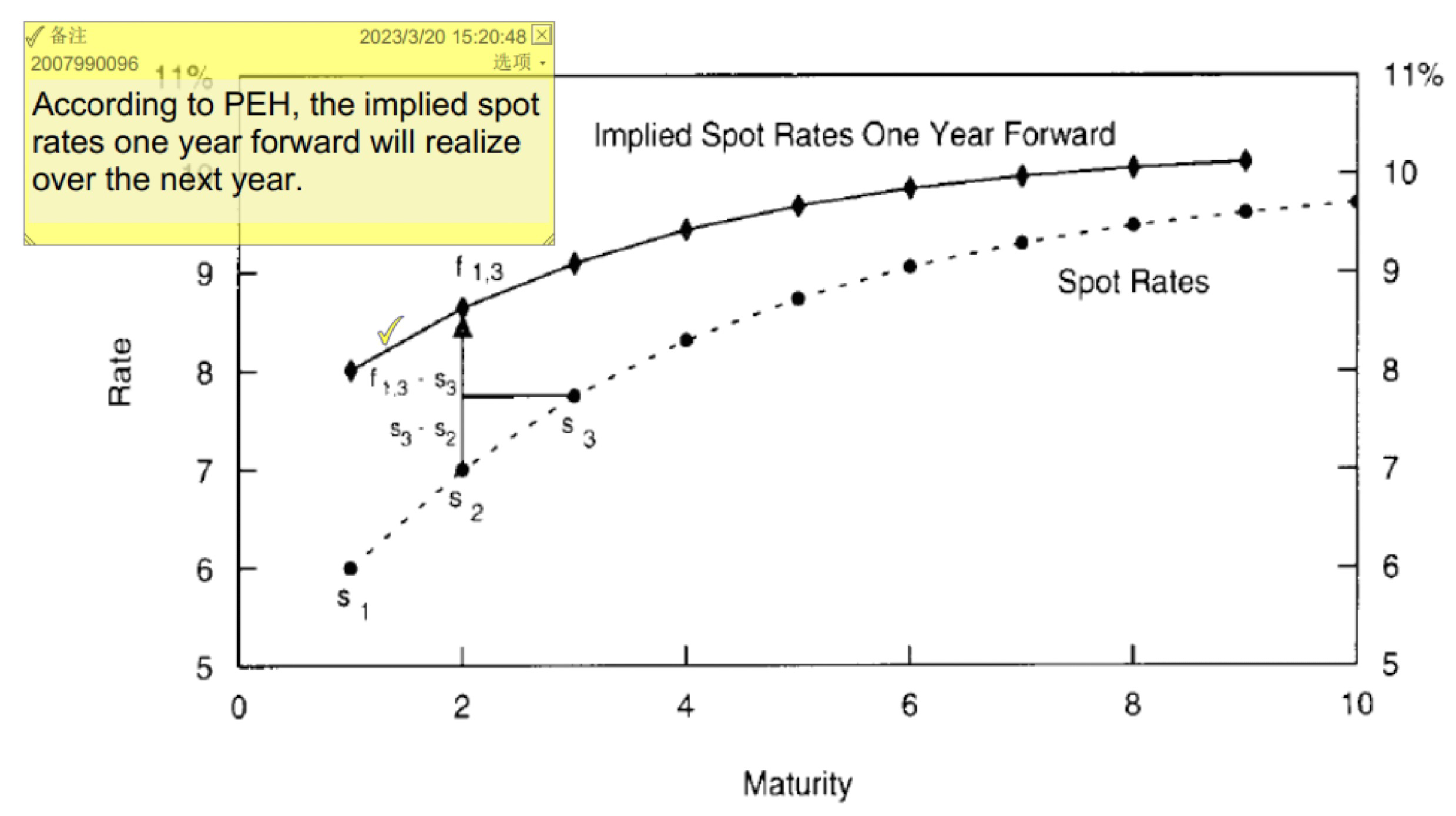
- 这一部分是在期望假设下的回报率
- 例子:
- 假设3年期债券 zero-coupon
- $$P_0=\frac{1}{(1+s_3)^3}$$
- $$P_1=\frac{1}{(1+f_{1,3})^2}$$
- $$\text{thus, }\frac{P_1}{P_0}=\frac{(1+s_3)^3}{(1+f_{1,3})^2}=1+s_1$$
- 这里就是一年期spot rate
Risk Premium Hypothesis (RPH)
- the forward rate reflects a bond’s expected return (due to embedded risks)
- Implication 1: there are no expected changes in the spot rates.
- Implication 2: An $n$-year bond will receive a one-year return of $f_{n-1, n}$, called rolling yield.
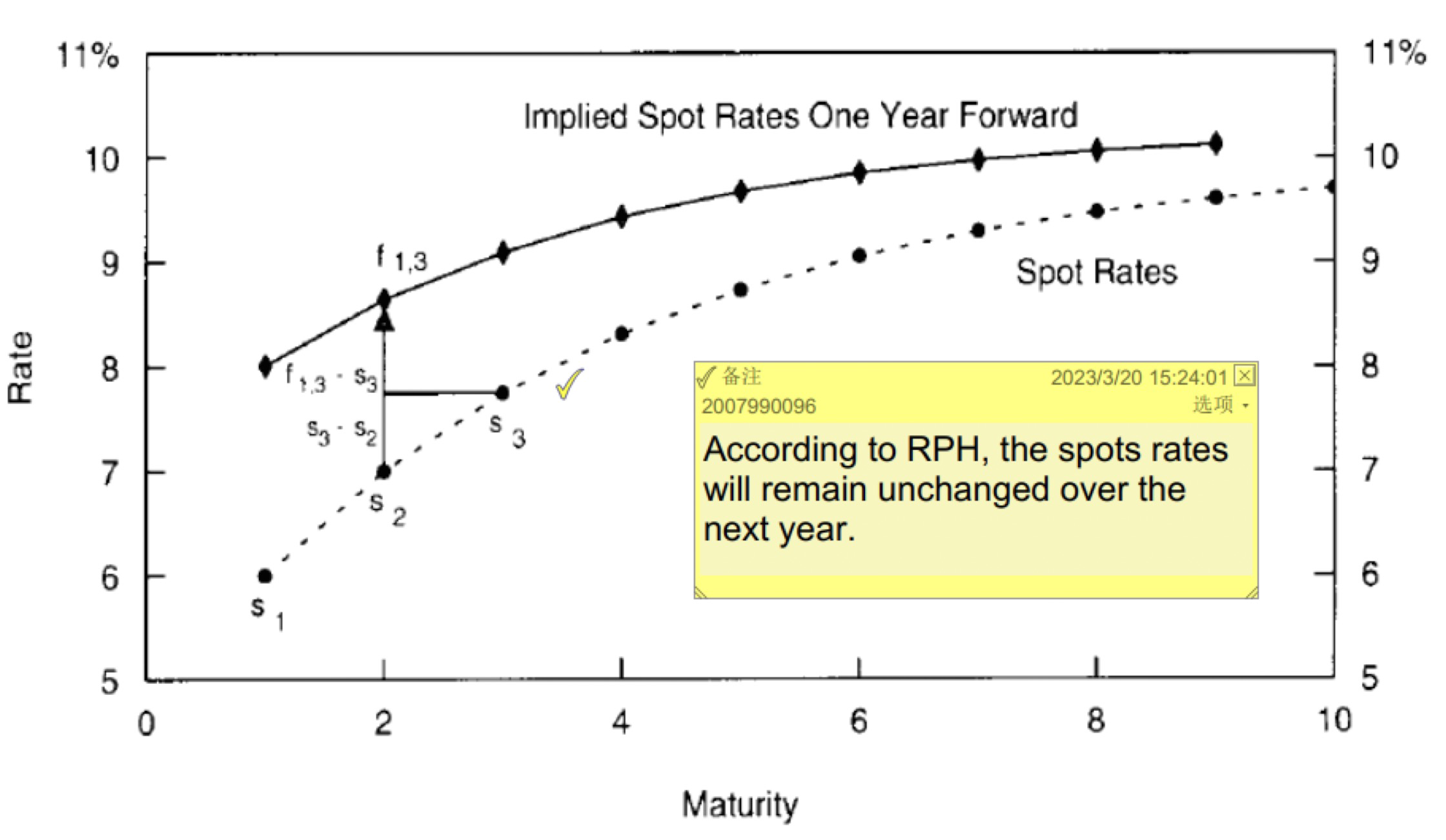
- 这一部分是在term structure不变的情况下的收益率
- 例子:
- 假设5年期债券,term structure 不变
- $$P_0=\frac{1}{(1+s_5)^5}$$
- $$P_1=\frac{1}{(1+s_4)^4}$$
- $$\text{thus, }\frac{P_1}{P_0}=\frac{(1+s_5)^5}{(1+s_4)^4}=1+f_{4,5}$$
- 这就是 rolling yield
put together
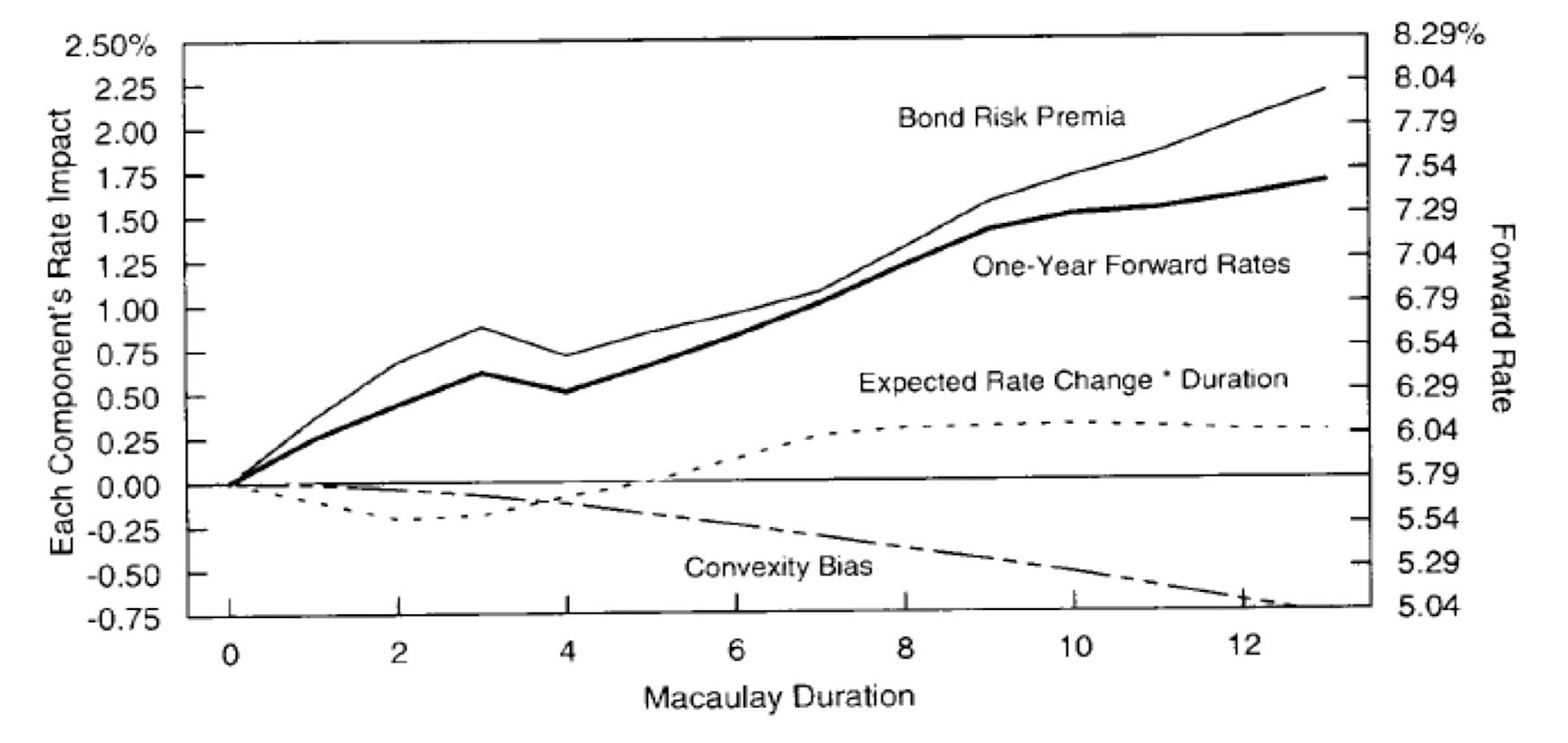
- The yield change implied by forwards can be split to an expected change in the $n-1$-year spot rate over the next year $E\left(\Delta S_{n-1}\right)$ and a bond risk premium $B R P_n$ :$$f_{1, n}-s_{n-1}=E(\Delta S_{n-1})+B R P_n$$where $B R P_n$ is the expected return of an $n$-year bond during the next year over the riskless one-year rate.
- The PEH assumes $B R P_n=0$.
- The RPH assumes $E(\Delta S_{n-1})=0$.
- 将收益率拆分成了两部分
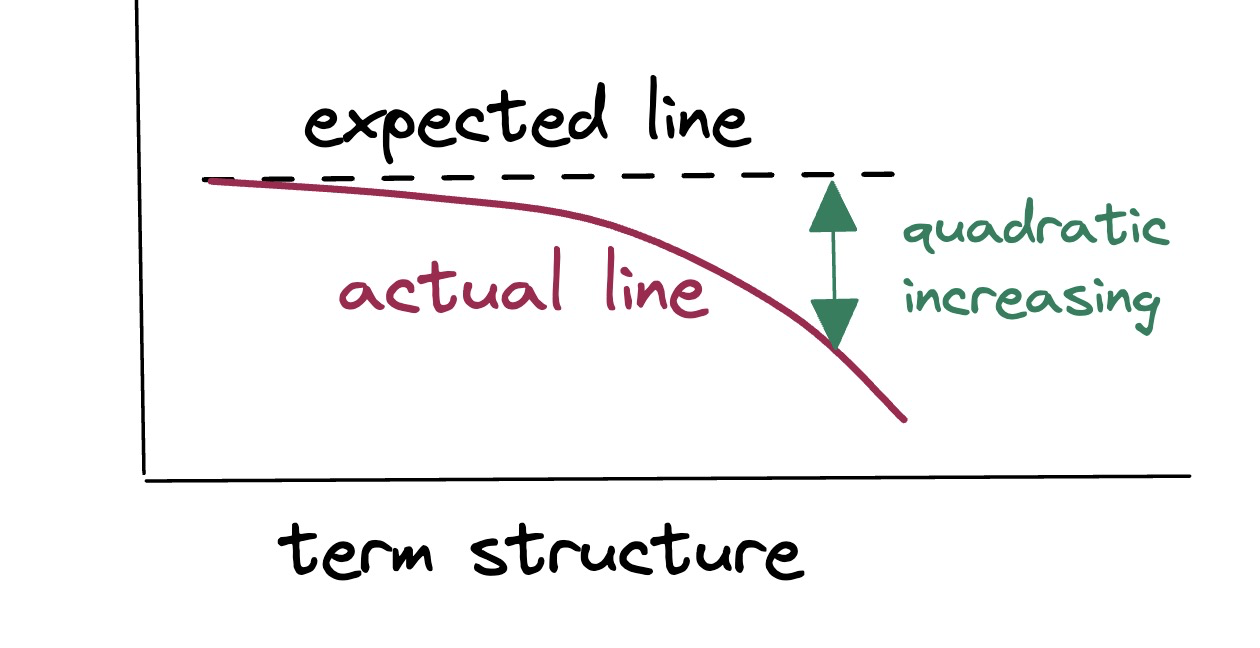
Impact of Convexity
- Convexity differentials across bonds tend to make the Treasury yield curve inverted or “humped.”
Convexity Bias
- Convexity-Adjusted Expected Return $=$ Rolling Yield + Convexity Value,
- Rolling Yield $=f_{n-1, n}$;
- Convexity Value $\approx-0.5 \times$ convexity $\times(\operatorname{Vol}(\Delta y))^2$.
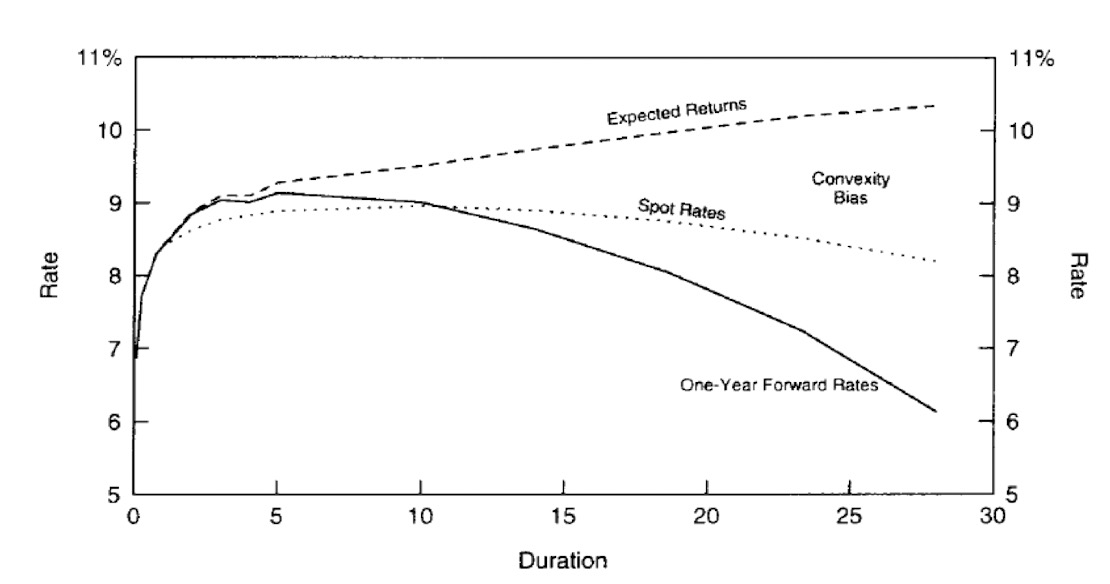
Implications of Convexity
- If an investor wants to assess a barbell-bullet trade’s relative cheapness, she needs to trade off the rolling yield give-up versus the convexity pick-up. The convexity-adjusted expected return provides a single number to measure the attractiveness of these trades.
- Typical barbell-bullet trades are more curve flatting trades than convexity trades. It is more likely that a given rolling yield disadvantage is offset by curve flattening than by the barbell’s convexity advantage.
Put all together
- $$\text{Rolling Yield} =\text{Short-Term Rate} + \text{Bond Risk Premium} + \text{Duration} \times E(\Delta s_{n-1})+ \text{Convexity Bias}$$where
- Rolling Yield $=f_{n-1, n}$;
- Short-Term Rate $=s_1$;
- Bond Risk Premium $=E(h_n-s_1)$;
- Convexity Bias $=-0.5 \times$ convexity $\times(\operatorname{Vol}(\Delta s_{n-1}))^2$;
将yield分层。
其中duration和convexity是泰勒展开项。
每一项都是可计算的,quantifiable。
L7: Interest rate modeling
- Why interest rating modeling?
- 定价现金流量取决于未来利率的变动的固定收益证券。
- Which rate to model?
- Most interest rate models are based on the (hypothetical) instantaneous spot rate—short rate.
- It can be thought of as a very short-term spot rate (e.g., overnight), though formally, it is for an instantaneous maturity.
- Some models work with forward rates, such as Heath, Jarrow, and Morton
The short rate is usually assumed to follow a stochastic process (Brownian motion):
- 一个随机游走过程
- $$d r_t=\mu(t) d t+\sigma(t) d W_t$$
Primer on Stochastic process
We consider a random variable $W$ whose value changes continuously.
In discrete-time, the change in $W$ in a small interval of time $\Delta t$ is $\Delta W$
We say that the variable $W$ follows a Wiener process (standard Brownian motion) if
- $\Delta W=\varepsilon \sqrt{\Delta t}$, where $\varepsilon$ is a random draw from a standard normal distribution $N(0,1)$;
- the values of $\Delta W$ in two different time intervals are independent.
Then we have the following properties:$$\begin{aligned}E[W(T)-W(t)] & =0 \\ V A R[W(T)-W(t)] & =T-t\end{aligned}$$
- where $t$ and $T$ denote the current and future time, respectively.
A Wiener process $W$ has a drift rate of 0 and a variance rate of 1 .
In general, if a random variable $x$ follows a generalized Wiener process, stochastic process, or Brownian motion:$$\Delta x=\mu \Delta t+\sigma \Delta W=\mu \Delta t+\sigma \mathcal{E} \sqrt{\Delta t}$$where the drift $\mu$ and the volatility $\sigma$ can be constants.
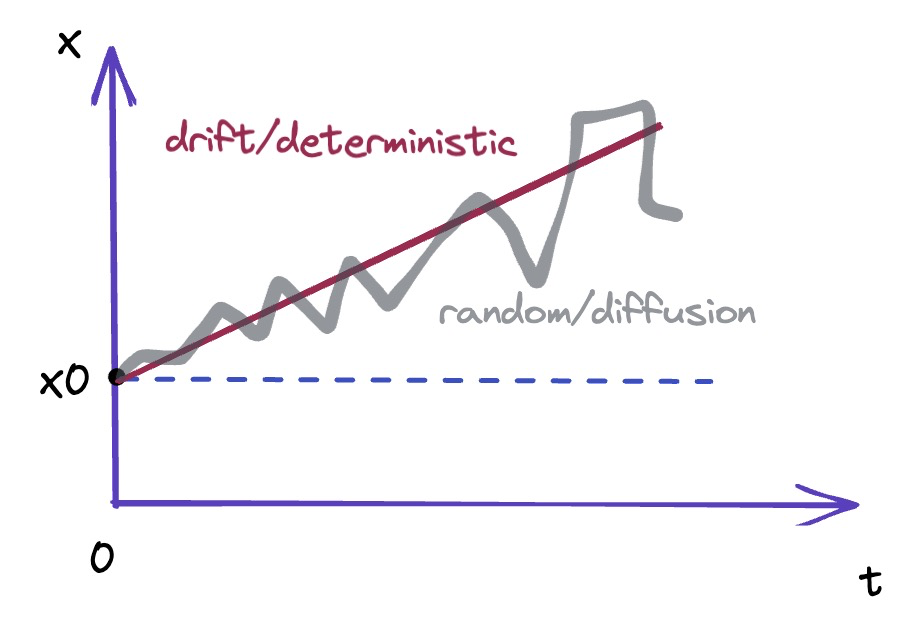
We have the following properties:$$\begin{aligned}E[\Delta x] & =\mu \Delta t \\ \operatorname{Var}(\Delta x) & =\sigma^2 \Delta t \end{aligned}$$
这个随机过程的目的
- We intend to build a realistic model to describe the underlying source of risk, e.g., interest rate fluctuation (default risk later);
- The model provides us with the probability distribution of outcomes at an important future time, e.g., expiration date of an option;
- If we assume stock price follow a geometric brownian motion, which means the return following a Brownian motion
- This probability distribution will allow us to compute the expected value of a security/derivative at the future time and subsequently its present value (price) via discounting.
Various short rate process
- Long-term trend and negative interest rates:$$r_t=\mu(t) d t+\sigma(t) d W_t$$
- 正常的随机游走
- Mean reversion (the Ornstein-Uhlenbeck process):$$d r_t=\kappa(\mu-r_t) d t+\sigma d W_t$$
- 其中 $\mu$ 是长期interest rate, $\kappa$ 是回归长期的速度,这种process随着时间变化总是围绕着长期利率波动
- Mean reversion and non-negative interest rate:$$d r_t=\kappa(\mu-r_t) d t+\sigma \sqrt{r} d W_t$$
- 在diffusion中添加了控制项,这样在 r 趋近于0时,波动项也趋近于0,只剩下了主项,这个过程中r永远非负。
- Geometric Brownian motion with time-varying drift and volatility:$$d \ln r(t)=[\theta(t)-\frac{\partial \sigma(t) / \partial t}{\sigma(t)} \ln r(t)] d t+\sigma(t) d W_t$$
- 每一种不同的process会有不同的数学性质,产生不同的解
- 首先需要明确采用什么随机过程
- 可能有解析解或者只能数值解
Desirable properties of an interest rate model
- Economic soundness,
- 例如:non-negativity of interest rate, mean reversion;
- Reasonable distribution of spot rates at a given maturity;
- Correlation structure between interest rates of different maturities;
- Volatility structure of interest rates,
- e.g., rate level-dependent volatility;
- Tractability (analytical solution versus numerical solution).
- 更倾向于有解析解的,更方便
Trade-offs
- All these desirable properties will never fit into one model!
- Which of these properties are necessary to squeeze into one model depends on the application.
- For example, it is more important to get the volatility structure right for pricing short-term derivatives rather than properly capturing mean reversion.
Models–Closed form
Vasicek model
- 最简单的解析解
- If the short rate follows a Brownian motion
- $$d r_t=\kappa(\mu-r_t) d t+\sigma d W_t$$
- then a zero-coupon bond’ price can be expressed as $$P(0, T)=A(T) e^{-B(T) r_0}$$where
- $$A(T)=exp{[\frac{(B(T)-T)(\kappa^2 \mu-\sigma^2/2)}{\kappa^2}-\frac{\sigma^2 B^2(T)}{4 \kappa}]}$$
- $$B(T)=\frac{1-e^{-\kappa T}}{\kappa}$$
- 如何应用
- 根据已知$P(0,T)$ 来估算式子中的三个变量(bootstraping and interpolation)
- 根据估出来的值来给别的定价
- 主要性质
- Continuous-time one factor model
- Allows negative interest rates
- Relatively simple, allowing closed-form solution
- Not for perfect calibration
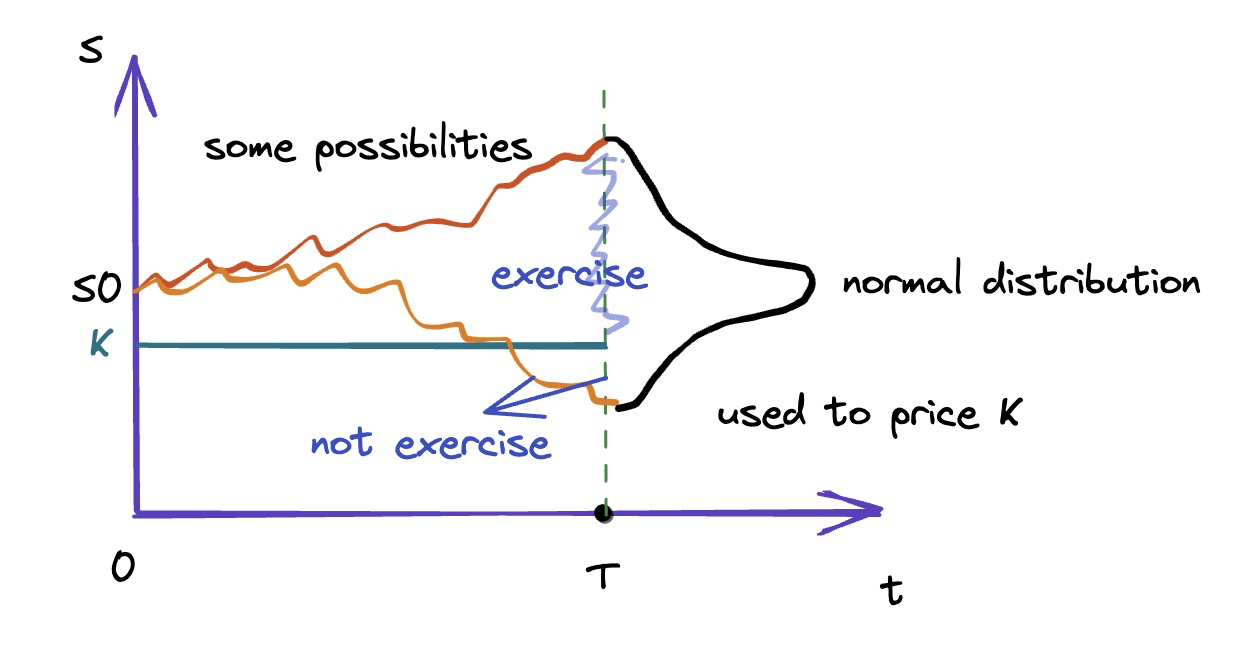
Pricing interest rate derivatives: an example
- Consider a European call option on a zero-coupon bond with the following information:
- $F$ is the face value of the underlying bond, $P(0, T)$ is the price of the discount bond maturing at time $T$
- $X$ is the strike price of the call option, $P(0, \tau)$ is the price of a discount bond maturing on the option’s expiration time $\tau$
- $N(\cdot)$ represents the cumulative standard normal distribution function
- $\sigma_P$ is the underlying bond’s price volatility. $\sigma$ is the spot rate’s volatility.
- $$\sigma_P=\frac{\sigma}{\kappa}(1-e^{-\kappa(T-\tau)}) \sqrt{\frac{1-e^{-2 \kappa \tau}}{2 \kappa}}$$
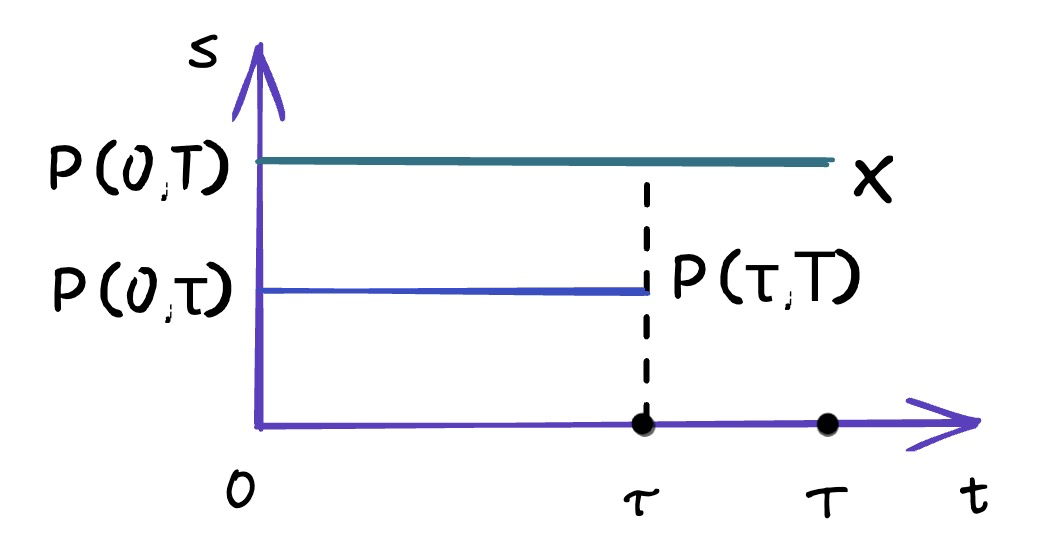
- 注:这种写法$P(0,T)$ 暗示了是simple discount
- Vasicek: short rate $\rightarrow$ underlying bond $\rightarrow$ price of option
- Black-Scholes: underlying bond $\rightarrow$ price of option
- Vasicek通过两层推出期权价格
Contrast: Vasicek and BS
- ==Vasicek (1977)==
- 期权定价模型 call option
- $$c=P(0, T) N(d)-X \cdot P(0, \tau) N(d-\sigma_P)$$
- 两个 N loosely 理解成执行两者的概率
- where$$d=\frac{1}{\sigma_P} \ln (\frac{P(0, T)}{P(0, \tau) X})+\frac{1}{2} \sigma_P$$
- Interpretation(loosely):$$c=P(0, \tau) E[\max (P(\tau, T)-X, 0)]$$
- ==Black-Scholes-Merton (1973)==
- $$c=S \cdot N(d)-X e^{-r T} N(d-\sigma \sqrt{T})$$
- where $$d=\frac{\ln (\frac{S}{x})+(r+\frac{\sigma^2}{2}) T}{\sigma \sqrt{T}}$$
- Interpretation: $$c=e^{-r T} E[\max (S^T-X, 0)]$$
The Cox-Ingersoll-Ross model
- If the short rate follows a Brownian motion:
- $$d r_t=\kappa(\mu-r_t) d t+\sigma \sqrt{r} d W_t$$
- then a zero-coupon bond’s price is expressed as$$P(0, T)=A(T) e^{-B(T) r_0}$$where$$\begin{aligned}& A(T)=(\frac{2 \gamma e^{(\kappa+\gamma+\lambda) \frac{T}{2}}}{2 \gamma+(\kappa+\gamma+\lambda)(e^{\gamma T}-1)})^{\frac{2 \kappa \mu}{\sigma^2}} \\ & B(T)=\frac{2(e^{\gamma T}-1)}{2 \gamma+\kappa+\gamma+\lambda)(e^{\gamma^T}-1)} \\ & \gamma=\sqrt{(\kappa+\lambda)^2+2 \sigma^2}\end{aligned}$$
- CIR 是证券定价模型,CRR是股票定价模型
- 四个参数待估计: $\kappa, \mu, \sigma$,$\lambda$.
- CIR模型的主要性质:
- Continuous-time one factor model
- Rules out negative interest rates
- Allows derivation of analytical formulae for derivatives prices
- Not for perfect calibration
Models–Numerical Method
- cost is high
Tree-based (lattice)model
Illustration
Backward Induction-Solving the tree model staring from a bond’s maturity backward for its price.
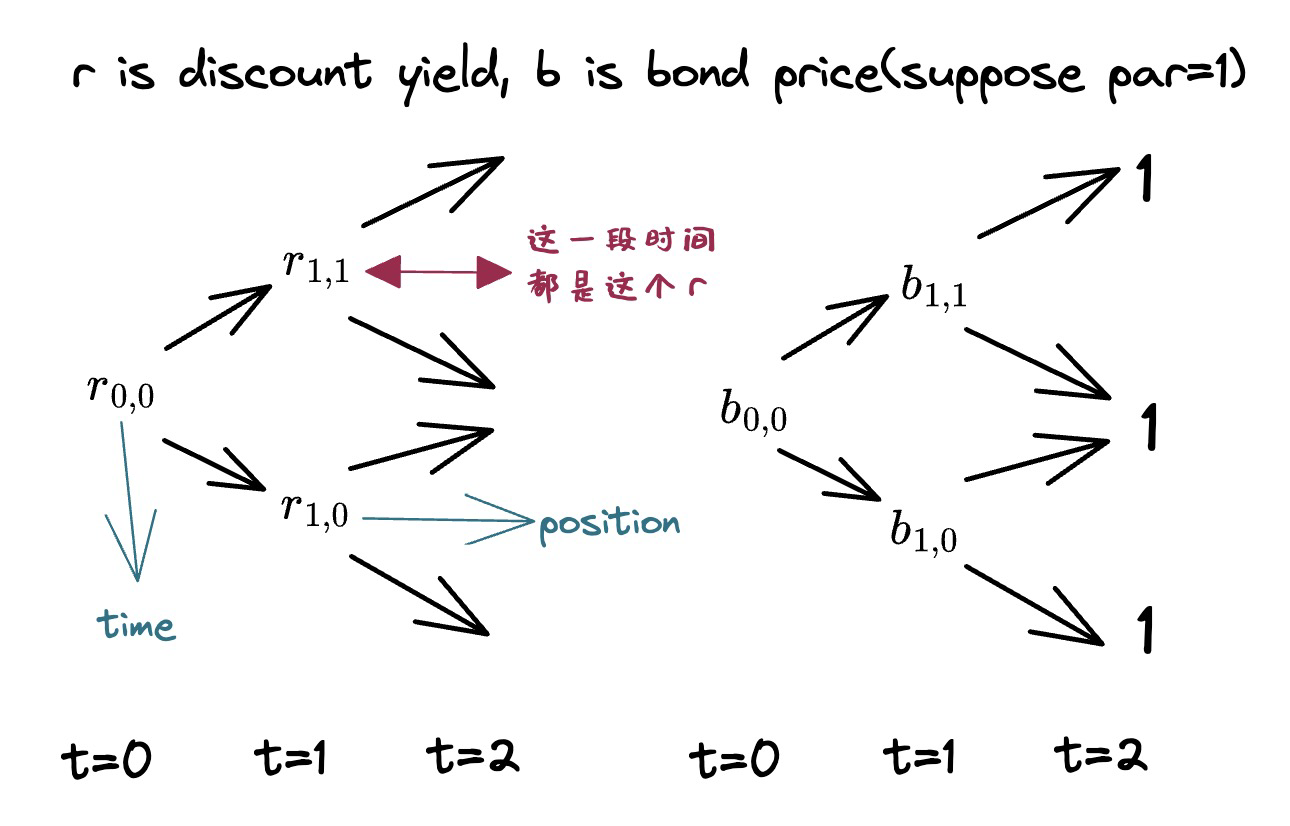
At time 2: $\quad b_{2,2}=\frac{1}{1+r_{2,2}} ; b_{2,1}=\frac{1}{1+r_{2,1}}$
At time 1: $\quad b_{1,1}=\frac{1}{1+r_{1,1}} E[b_2]=\frac{1}{1+r_{1,1}}[0.5 b_{2,2}+0.5 b_{2,1}]$
With the short rate tree, we have computed the discount bond prices!
- longer-term spot rates $(\sqrt{ })$
- forward rates $(\sqrt{ })$
- 如何构造short rate?
- 使用BDT model(见下)
Black-Derman-Toy Model
- We first need to specify a short rate process.
- The Black-Derman-Toy model assumes the short rate follows a Geometric Brownian motion:$$d \ln r(t)=[\theta(t)-\frac{\partial \sigma(t) / \partial t}{\sigma(t)} \ln r(t)] d t+\sigma(t) d W_t$$
- 两项都和t有关
- 该式子两侧有可能小于0,但 r 一定大于0
- The BDT model is a popular short rate model used in the pricing of bond options, swaptions, and other interest rate derivatives.
- 如果short rate 服从 Geometric Brownian motion:$$\ln r(t+1)=\ln r(t)+\theta \pm \sigma \Leftrightarrow r(t+1)=r(t) e^{\theta \pm \sigma}$$
- 排除了负利率的情况
- 如果short rate 服从Brownian motion (as in the Vasicek and CIR models):$$r(t+1)=r(t)+\theta \pm \sigma$$
- 通常在二叉树中上下的概率都是50%
注
- ==对于bond,年化波动率大概在10%-20%之间==
- ==对于stock,年化波动率大概在50%左右==