概率论与数理统计笔记

概率论

L1: 集合

• 集合：或叫 “空间” “样品空间”
• “样品空间”：$\Omega$ , 元素用 $\omega_1, \omega_2$ 表示
• “空集”： $\emptyset$
• 符号: $A \subset \Omega, A \subseteq \Omega$.
• $$A=B \Leftrightarrow A \subseteq B, B \subseteq A$$
  • 例: 偶数集 $={x \in \mathbb{R}: \sin (\pi x / 2)=0}$.

集合运算

• 余集： $A^c=\Omega \backslash A$

• 交换律：

  • $A \cap B=B \cap A$
  • $A \cup B=B \cup A$

• 结合律：

  • $(A \cap B)\cap C=A\cap(B \cap C)$
  • $(A \cup B)\cup C=A\cup(B \cup C)$

• 分配律：

  • $(A \cap B)\cup C=(A\cup B) \cap (A\cup C)$
  • $(A \cup B)\cap C=(A\cap B) \cup (A\cap C)$

• De Morgen:

  • $(A\cap B)^c=A^c\cup B^c$
  • $(A\cup B)^c=A^c\cap B^c$

• 对称差：

  • $A\Delta B=(A\backslash B)\cup (B\backslash A)$

• 若A交B为空

  • $A+B=A\cup B$

• 特征函数

  • $$I_A(\omega)= \begin{cases} 1 & \text{若属于A} \\ 0 & \text{若不属于 A}\end{cases}$$

• 记号，

  • $$\begin{aligned} & a \vee b=\max {a, b} \\ & a \wedge b=\min {a, b} .\end{aligned}$$

定理

• $$
  \begin{aligned}
  I_{A \cap B} & =I_A \times I_B=I_A \wedge I_B, \\
  I_{A \cup B} & =I_A \vee I_B, \\
  I_{A \cup B}+I_{A \cap B} & =I_A+I_B .
  \end{aligned}
  $$
• $$(A\Delta B)\Delta C=A \Delta (B\Delta C)$$

有限样本空间上概率的定义

• 满足三个条件：
  • 非负性
    • 对每个定义域内的点概率都大于等于0
  • 正规化
    • 全集加起来的概率是1
  • 有限可加性
    • 对不相交的A，B，$P(A)+P(B)=P(A+B)$

可数样本空间上概率的定义

• 满足三个条件：
  • 非负性
    • 对每个定义域内的点概率都大于等于0
  • 正规化
    • 全集加起来的概率是1
  • 可数可加性
    • 对任意不相交的 $A_n$，$P(\bigcup_{n=1}^{\infty} A_n)=\sum_{n=1}^{\infty} P(A_n)$

概率的性质

• 设P是有限样本空间上的概率
• 对任意 $A, B \subset \Omega$, 均有$$P(A \cup B)+P(A \cap B)=P(A)+P(B)$$

• 若 $A \subset B$, 则 $P(A) \leq P(B)$;
• 对每个 $A \subset \Omega$, 有 $0 \leq P(A) \leq 1$;
• 对两两不相交的 $A_1, A_2, \cdots, A_n \subset \Omega$, 均有$$P(A_1+A_2+\cdots+A_n)=\sum_{k=1}^n P(A_k)$$
• 对任意 $A_1, A_2, \cdots, A_n \subset \Omega$, 均有$$P(A_1 \cup A_2 \cup \cdots \cup A_n) \leq \sum_{k=1}^n P(A_k)$$

L2:

独立事件

• 定义:一个事件就是概率P定义域F中的一个点,即样本空间$\Omega$的一个可测子集A,使得$P(A)$有意义。
• 若两个事件独立，则 $P(A\cap B)=P(A)P(B)$
• 更一般的，$P(A_1\cap \cdots \cap A_n)=P(A_1)\cdots P(A_n)$
  • 注：例如若A，B，C独立，则需要同时满足（A，B），（A，C），（B，C），（A，B，C）

概率计算

• 抽样问题
• 分配问题

L3:

随机变量（在可数集上）

• $\Omega$ 是一个样本空间（有限或者无限都可以）

• 定义在这个空间上的一个数值函数X，称为一个随机变量，记为$X(\omega)$

• 特点：

  • X是一个数值函数
  • 定义域是样品空间

• 若X,Y是随机变量，则

  • $X+Y,X\times Y$ 等基本运算都是随机变量

分布

• 设 $A$ 是一个由某些实数构成的集合, 定义
  • $$P(X \in A)=P({\omega: X(\omega) \in A})$$
• 注意: 集合 ${\omega: X(\omega) \in A}$ 是一个可数集, 属于 $P$ 的定义域（因为这里假设 $\Omega$ 是一个可数样本空间, 不可数样品空间后面讨论）。
• 例: $A={x}$ 只含一点 $x$, 记$$P(X=x)=P(X \in{x})$$
• 定义（分布）: 称函数$$F_X(x)=P(X\leq x)$$为随机变量 $X$ 的分布函数。显然,
  • $$P(a<X \leq b)=P(X \leq b)-P(X \leq a)=F_X(b)-F_X(a)$$

性质

• $F$ 是单增的: 若 $x_1<x_2$, 则 $F(x_1) \leq F(x_2)$ 。
• $F(-\infty)=0$ 和 $F(+\infty)=1$ 。
• 右连续:$$F(x+0)=F(x)=\lim _{k \rightarrow \infty} P(X \leq x+\frac{1}{k})$$和左极限存在:
  $$
  F(x-0)=\lim _{k \rightarrow \infty} P\left(X \leq x-\frac{1}{k}\right)
  $$
  但可能 $F(x+0) \neq F(x-0)$ 。

期望

• $$E(X)=\sum_{\omega\in\Omega}X(\omega)P({\omega})$$
• 若 $X$ 是一个随机变量, 则 $\varphi(X)$ 也是一个随机变量, 其数学期望 $E(\varphi(X))$ 为$$E(\varphi(X))=\sum_{\omega \in \Omega} \varphi(X(\omega)) P({\omega})$$
• 特别地, $\varphi(x)=x^r$,$$E(\varphi(X))=\sum_{\omega \in \Omega}[X(\omega)]^r P({\omega})$$称为 $X$ 的第 $r$ 阶力矩。

期望性质

• $E(c)=c$
• $E(X+Y)=E(X)+(Y)$
• $E(aX)=aE(X)$
• $E(X)<E(y)\quad \text{ if X < Y}$

L4:

密度函数

• 定义在$R=(-\infty,\infty)$ 上的函数称为密度函数
• 满足：任意点大于0，在空间上积分为1

具有密度的随机变量

• 定义: 设 $X$ 是样品空间 $\Omega$ 上的函数, 如果其概率由一个密度函数 $f$ 决定，即$$P(a<X \leq b)=\int_a^b f(u) d u$$或更一般，如果对由若干有限或无限区间构成的集合 $A$,$$P(X \in A)=\int_A f(u) d u$$则称 $X$ 为具有密度函数的随机变量（有时称为连续的随机变量, 相对前面离散的随机变量）。
• 若 $A=(-\infty, x)$, 则$$F(x)=P(X \leq x)=\int_{-\infty}^x f(u) d u$$它是 $X$ 的分布函数。若 $f$ 连续, 则 $F^{\prime}(x)=f(x)$ 。

二元分布函数

• 一元分布函数：$F(x)=P(X<x)$
• 二元分布函数：$F(x,y)=P(X\leq x,Y\leq y)$
• 若存在函数$f(u,v)$ 使得$$F(x,y)=P(X\leq x,Y\leq y)=\int_{-\infty}^x\int_{-\infty}^yf(u,v)dudv$$
  • 称 $f(u,v)$ 为二元随机变量$(X,Y)$的联合密度

性质

• 关于每个分量是单调递增
• 关于每个分量是有连续的，左极限存在
• $0\leq F(x,y)\leq 1$

• $P((X, Y) \in S)=\iint_S f(u, v) d u d v$
• 数学期望 $E(\varphi(X, Y))$
  $$E(\varphi(X, Y))=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \varphi(u, v) f(u, v) d u d v$$

条件概率

• 设 $A, S \subset \Omega$, 定义$$P(A \mid S):=\frac{P(A S)}{P(S)}=\frac{P(A \cap S)}{P(S)}$$称此值为 $A$ 相对 $S$ 的条件概率。

公式

• 命题1: 对任意事件 $A_1, A_2, \cdots, A_n$, 有$$P(A_1 A_2 \cdots A_n)=P(A_1) P(A_2 \mid A_1) P(A_3 \mid A_1 A_2)\cdots P(A_n \mid A_1 A_2 \cdots A_{n-1})$$这里假设 $P\left(A_1 A_2 \cdots A_{n-1}\right)>0$ 。
• 命题2: 设 $\Omega=\sum_n A_n$ 是样品空间不相交的分割, 则对任意 $B$,$$P(B)=\sum_n P(A_n) P(B \mid A_n)$$
• 命题3（Bayes 定理, 1763）: 设命题2条件成立, 若 $P(B)>0$, 则$$P(A_n \mid B)=\frac{P(A_n) P(B \mid A_n)}{\sum_k P(A_k) P(B \mid A_k)}$$

L5:

随机变量的独立性

• 独立随机变量: 取可数值的随机变量 $X_1, X_2, \cdots, X_n$ 是独立的, 若对任意实数 $x_1, x_2, \cdots, x_n$, 有$$P(X_1=x_1, \cdots, X_n=x_n)=P(X_1=x_1) \cdots P(X_n=x_n)$$

命题

• 命题1: 设取可数值的随机变量 $X_1, X_2, \cdots, X_n$ 是独立的, 则对任意可数集 $S_1, S_2, \cdots, S_n$ :$$P(X_1 \in S_1, \cdots, X_n \in S_n)=P(X_1 \in S_1) \cdots P(X_n \in S_n)$$
• 命题2：设取可数值的 $X_1,X_2,\cdots$ 是独立的，则事件$${X_1\in S_1 },{X_2\in S_2} \cdots$$是独立的。
• 命题3: 设取可数值的随机变量 $X_1, X_2, \cdots, X_n$ 是独立的, $\varphi_1, \varphi_2, \cdots, \varphi_n$ 是定义在 $(-\infty, \infty)$ 上的任意实值函数, 则随机变量$$\varphi_1(X_1), \varphi_2(X_2), \cdots, \varphi_n(X_n)$$是独立的。

定义

• 定义: 称对一般的随机变量 $X_1, X_2, \cdots, X_n$ 是独立的, 当且仅当对任意实数 $x_1, x_2, \cdots, x_n$, 事件$${X_1 \leq x_1},{X_2 \leq x_2}, \cdots,{X_n \leq x_n}$$是独立的。特别地,$$P(X_1 \leq x_1, \cdots, X_n \leq x_n)=P(X_1 \leq x_1) \cdots P(X_n \leq x_n)$$即用分布函数的语言:$$F(x_1, \cdots, x_n)=F_1(x_1) \cdots F_n(x_n)$$
• 或者, 用密度函数的语言：$$\begin{aligned}P(X_1 \in S_1, \cdots, X_n \in S_n) ={\int_{S_1} f_1(u) d u} \cdots{\int_{S_n} f_n(u) d u} =\int_{S_1} \cdots \int_{S_n} f_1\left(u_1\right) \cdots f_n\left(u_n\right) d u_n \cdots d u_1\end{aligned}$$但左边等于$$\int_{S_1} \cdots \int_{S_n} f\left(u_1, \cdots, u_n\right) d u_n \cdots d u_1$$所以,$$f(u_1, \cdots, u_n)=f_1(u_1) \cdots f_n(u_n)$$

L6:

• $$\color{red}{E(I_A)=P(A)}$$
• 对任意集合 $A_1, A_2, \cdots, A_n$, 下列等式成立:
  • 庞加莱公式
  • $$\begin{aligned}P(\cup_{j=1}^n A_j) =\sum_j P(A_j)-\sum_{j, k} P(A_j A_k)+\sum_{j, k, l} P(A_j A_k A_l) -\cdots+(-1)^{n-1} P(A_1 A_2 \cdots A_n)\end{aligned}$$
  • 其中求和的指标不同、取值从1到n。特别地,
    • $$P(A_1 \cup A_2)=P(A_1)+P(A_2)-P(A_1 \cap A_2)$$
    • $$P(A_1 \cup A_2 \cup A_3)={P(A_1)+P(A_2)+P(A_3)} -{P(A_1 A_2)+P(A_1 A_3)+P(A_2 A_3)}+P(A_1 A_2 A_3)$$

L7:

方差和协方差

• X和Y是独立可积变量，则
  • $$E(XY)=E(X)E(Y)$$

力矩

• 对任意正整数r，$E(X^r)$ 称为随机变量的第r阶力矩。
• r=1，期望
• r=2，重要情况
  • 令 $X^0=X-E(X)$
  • 则 $X^0$ 的二阶力矩为X的方差， $Var(X)=E((X-E(X))^2)$
  • $\sigma(X)$ 为偏差（标准差）

方差

• 定理：若 $E\left(X^2\right)<\infty$, 则 $E(|X|)<\infty$, 且$$\sigma^2(X)=E\left(X^2\right)-[E(X)]^2$$从而 ${E(|X|)}^2 \leq E\left(X^2\right)$ 。

• 方差的意义：随机变量与均值间的平均偏差。

• 定理：若 X, Y 独立，方差均有限，则

  • $$\sigma^2(X+Y)=\sigma^2(X)+\sigma^2(Y)$$

• Cauchy-Schwarz 不等式：设 X,Y 为任意随机变量，则

  • $$[E(XY)]^2\leq E(X^2)E(Y^2)$$

协方差

• 协方差 $$E(X^0Y^0)=Cov(X,Y)=E(XY)-E(X)E(Y)$$
• 关联系数为$$\rho(X,Y)=\frac{E(X^0Y^0)}{\sqrt{E{(X^0)^2}E{(Y^0)^2}}}$$
  • $$-1\leq \rho(X,Y) \leq 1$$
• 若 X,Y 独立，则关联系数为0；反之，关联系数为0，X,Y不一定独立

生成函数或母函数

• 设X是随机变量，取值为非负整数。概率决定如下：

  • $$P(X=j)=a_j$$

• 引入函数：

  • $$g(z)=a_0+a_1z+a_2z^2+\cdots =\sum_{j=0}^\infty a_jz^j$$
  • 此函数为随机变量X的母函数/生成函数，变量z可以取复数值。
  • z的绝对值小于1时，级数收敛。

• 可求导

• $$\begin{aligned}
  g^{\prime}(z) & =a_1+2 a_2 z+\cdots=\sum_{n=1}^{\infty} n a_n z^{n-1} \\
  g^{\prime \prime}(z) & =2 a_2+6 a_3 z \cdots=\sum_{n=2}^{\infty} n(n-1) a_n z^{n-2} \\
  g^{(j)}(z) & =\sum_{n=j}^{\infty} n(n-1) \cdots(n-j+1) a_n z^{n-j}
  \end{aligned}$$

  • 令 $z=0$, 得 $g^{(j)}(0)=j ! a_j$, 或 $a_j=\frac{1}{j !} g^{(j)}(0)$, 故从 $g$ 可得 $a_j$ 的值, 生成函数和分布两者一一对应。
  • 令 $z=1$, 得
    • $$g^\prime(1)=\sum_{n=1}^\infty n a_n=E(X)$$
    • $$g^{\prime \prime}(1)=\sum_{n=2}^\infty n(n-1) a_n=\sum_{n=0}^\infty n^2 a_n-\sum_{n=0}^\infty n a_n=E(X^2)-E(X)$$
  • 故
    • $$\begin{aligned}

& E(X)=g^{\prime}(1), \quad E(X^2)=g^{\prime}(1)+g^{\prime \prime}(1) \\
& \sigma^2(X)=E(X^2)-(E(X))^2=g^{\prime}(1)+g^{\prime \prime}(1)-(g^{\prime}(1))^2
\end{aligned}$$

卷积

• 设 $Y$ 是另一个随机变量, 取值非负整数, 概率决定如下$$P(Y=j)=b_j, \quad j=0,1,2, \cdots$$

• 生成函数为 $h(z)=\sum_{j=0}^{\infty} b_j z^j$ 。问: 若 $X$ 和 $Y$ 独立, 求 $X+Y$ 的概率分布?

• 事实上,$$g(z) h(z)=(\sum_{j=0}^{\infty} a_j z^j)(\sum_{k=0}^{\infty} b_k z^k)=\sum_j \sum_k a_j b_k z^{j+k}$$令 $g(z) h(z)=\sum_{i=0}^{\infty} c_i z^i$ 得$$c_i=\sum_{j+k=i} a_j b_k=\sum_{j=0}^i a_j b_{i-j}$$

• 数列 $c_j$ 称为两个数列的卷积

  • 若 X 和 Y 独立，则
  • $$c_i=P(X+Y=i)$$

• 定理：若随机变量 $X_1,\cdots X_n$ 独立，生成函数分别为$g_1,\cdots g_n$ 则 $X_1+X_2+\cdots+X_n$ 的生成函数为 $g=g_1g_2\cdots g_n$

L8:

Laplace 变换

• $$E(e^{-\lambda x})=\int_{-\infty}^\infty e^{-\lambda u}f(u)du$$
• 称为随机变量的拉氏变换，其中f为X的密度函数

Fourier 变换

• 在拉氏变换中若$\lambda=-i\theta$ , 则$$E(e^{i\theta x})=\int_{-\infty}^\infty e^{i\theta u}f(u)du$$
  • 函数 $E(e^{i\theta x})$ 称为X的特征函数

Stirling公式

• 下列极限成立：$$\lim _{n \rightarrow \infty} \frac{n ! e^n}{n^{n+1 / 2}}=\sqrt{2 \pi}$$
• 即：
  • $$n!\sim \sqrt{2\pi}n^{n+1/2}e^{-n}$$
• 为后面的中心极限等定理推导铺垫。

L9:

• 定理1: 设 $0<p<1, q=1-p, A>0,|x_{n k}| \leq A$, 其中$$x_{n k}=\frac{k-n p}{\sqrt{n p q}}, \quad 0 \leq k \leq n$$则当 $n \rightarrow \infty$, 下列极限成立$$(\begin{array}{l}n \ k\end{array}) p^k q^{n-k} \sim \frac{1}{\sqrt{2 \pi n p q}} e^{-x_{n k}^2 / 2}$$
• De Moivre-Laplace 定理
  • 定理: 设掷硬币正面出现的概率为 $0<p<1$, 反面出现的概率为 $q$, $S_n$ 表示掷 $n$ 次硬币正面出现的次数, 则对任意实数 $-\infty<a<b<+\infty$,
  • $$\lim _{n \rightarrow \infty} P(a<\frac{S_n-n p}{\sqrt{n p q}} \leq b)=\frac{1}{\sqrt{2 \pi}} \int_a^b e^{-x^2 / 2} d x$$
  • 即趋近于正态分布

中心极限定理

引

• 先看bernoulli分布。

• 设 $X_j$ 是独立的Bernoulli随机变量, 令$$S_n=X_1+\cdots+X_n, \quad n \geq 1$$知 $E(X_j)=p, \sigma^2(X_j)=p q$, 且 $E(S_n)=n p, \sigma^2(S_n)=n p q$ 。令$$X_j^*=\frac{X_j-E(X_j)}{\sigma(X_j)} ; \quad S_n^*=\frac{S_n-E(S_n)}{\sigma(S_n)}=\frac{1}{\sqrt{n}} \sum_{j=1}^n X_j^*$$则$$\begin{array}{ll}
  E(X_j^*)=0, & \sigma^{(} X_j^*)=1, \\
  E(S_n^*)=0, & \sigma^{(} S_n^*)=1 .
  \end{array}$$

• 易知$$\begin{aligned}P(S_n=k) =P(S_n^*=x_{n k})=P(S_n^*=\frac{k-n p}{\sqrt{n p q}}) =(\begin{array}{l}n \ k\end{array}) p^k q^{n-k}\end{aligned}$$令 $P(S_n^* \leq x)=F_n(x)$ 。由De Moivre-Laplace定理

• 更一般

• 设 ${X_j, j \geq 1}$ 是独立的具有相同分布的随机变量 （不一定是Bernoulli分布）。令 $E(X_j)=m, \sigma^2(X_j)=\sigma^2$, 其中 $0<\sigma<\infty$ 。

• 设 $S_n, S_n^*$ 如前, 即$$S_n=X_1+\cdots+X_n, \quad S_n^*=\frac{S_n-E(S_n)}{\sigma(S_n)}$$知$$E(S_n)=n m, \sigma^2(S_n)=n \sigma^2$$同样，令$$X_j^*=\frac{X_j-E(X_j)}{\sigma(X_j)} ; \quad S_n^*=\frac{S_n-E(S_n)}{\sigma(S_n)}=\frac{1}{\sqrt{n}} \sum_{j=1}^n X_j^*$$则一样成立下列式子:$$\begin{array}{ll}E(X_j^*)=0, & \sigma^{(} X_j^*)=1, \\ E(S_n^*)=0, & \sigma^{(} S_n^*)=1\end{array}$$

定理

• 定理 （中心极限）: 设 $S_n, m, \sigma^2$ 如上, 则对任意实数$-\infty<a<b<+\infty$
• $$\lim _{n \rightarrow \infty} P(a<\frac{S_n-n m}{\sqrt{n} \sigma} \leq b)=\frac{1}{\sqrt{2 \pi}} \int_a^b e^{-x^2 / 2} d x$$
• 即
  • $$\lim_{n \rightarrow \infty} P(a<\frac{S_n-E(S_n)}{\sigma_{S_n}}\leq b)=\frac{1}{\sqrt{2\pi}} \int_a^b e^{-x^2/2}dx$$
• $S_n=X_1+X_2+\cdots+X_n$ 独立同分布
• 极限不依赖于$\theta$和$m$
• 中心极限定理可写成$$P(x_1 \sigma \sqrt{n}<S_n-m n<x_2 \sigma \sqrt{n}) \approx \Phi(x_2)-\Phi(x_1)$$或者令 $x_2=x, x_1=-x$
  • $$P(|S_n-m n|<x \sigma \sqrt{n}) \approx \Phi(x)-\Phi(-x)=2 \Phi(x)-1$$
• 对于那些不属于正态分布的数据，根据中心极限定理，在样本容量很大时，总体参数的抽样分布是趋向于正态分布的，最终都可以依据正态分布的检验公式对它进行下一步分析。

L10:

大数定律

• 定理：设中心极限定理假设满足，独立，同分布，方差有限
• 则对任意常数 c>0, $$\lim _{n \rightarrow \infty}P(|\frac{S_n}{n}-m|<c)=1$$
• 意义：算术平均$S_n/n$在概率意义下收敛到一个常数$E(X_1)$

推广的大数定律

• 定理：设随机变量 ${X_j, j \geq 1}$ 独立, 满足$$E(X_j)=m_j, \quad \sigma^2(X_j)=\sigma_j^2$$且存在常数 $M<\infty$ 使得对所有 $j$,$$\sigma_j^2 \leq M$$则对任意固定常数 $c>0$,$$\lim _{n \rightarrow \infty} P(|\frac{S_n-s_n}{n}|<c)=1$$其中 $S_n=X_1+\cdots+X_n, \quad s_n=m_1+\cdots+m_n$
• 允许不同分布

Chebyshev不等式

• 定理：设随机变量X第2阶力矩有限，则对任意常数c>0,
• $$P(|X|\geq c)\leq \frac{E(X^2)}{c^2}$$

分布总结

Bernoulli分布

• 两点分布
• $P(X=1)=p$
• $P(X=0)=q=1-p$
• $E(X)=p,\quad \sigma^2(X)=p(1-p)=pq$
• 概率质量函数：
  • $f(k;p)=P(X=k)=p^k(1-p)^{1-k}$
• 生成函数：
  • $g(z)=q+pz$

二项式分布

• 设 $X_1,X_2,\cdots$ 是 n 个独立的服从bernoulli的分布
• 随机变量$S_n$ 为$$S_n=X_1+X_2+\cdots+X_n$$
• $S_n$ 满足二项分布
• 概率质量函数：
  • $$f(k;n,p)=P(S_n=k)=(\begin{array}{l}n \ k \end{array}) p^k(1-p)^{n-k}, \quad k=0,1, \cdots, n$$
• $E(S_n)=np,\quad \sigma^2(S_n)=npq$
• X 服从二项式分布，称为 $X \sim B(n,p)$
• 若 $X \sim B(n,p)$, $Y \sim B(m,p)$, 则 $X+Y \sim B(m+n,p)$
• 二项式分布的极限是poisson分布
• 生成函数：
  • $g(z)=(q+pz)^n$
• 矩母函数：
  • $$M(t)=E(e^{tX})=(q+pe^t)^n$$
• 特征函数：
  • $$\varphi(\omega)=E(e^{i\omega X})=(q+pe^{i\omega})^n$$

多项式分布

• 二次多项式(binomial):$$(x_1+x_2)^n=\sum_{k=0}^n(\begin{array}{l}n \ k\end{array}) x_1^k x_2^{n-k}=\sum_{k+j=n} \frac{n !}{k ! j !} x_1^k x_2^j$$
• 多次多项式(multinomial):$$(x_1+x_2+\cdots+x_r)^n=\sum_{k_1+\cdots+k_r=n} \frac{n !}{k_{1} ! k_{2} ! \cdots k_{r} !} x_1^{k_1} x_2^{k_2} \cdots x_r^{k_r}$$
  即 $k_1 \geq 0, \cdots, k_r \geq 0$ 为非负整数, 且和为 $n$ :
  $$
  k_1+\cdots+k_r=n
  $$

Poisson分布

• Poisson分布的模型: 给定一个常数 $\alpha>0$, 设$$a_k=\frac{e^{-\alpha}}{k !} \alpha^k, \quad k=0,1,2 \cdots$$则 $\sum_{k=0}^{\infty} a_k=\sum_{k=0}^{\infty} \frac{e^{-\alpha}}{k !} \alpha^k=e^{-\alpha} e^\alpha=1$, 其均值为$$\sum_{k=0}^{\infty} k a_k=e^{-\alpha} \sum_{k=0}^{\infty} \frac{k}{k !} \alpha^k=\alpha e^{-\alpha} \sum_{k=1}^{\infty} \frac{\alpha^{k-1}}{(k-1) !}=\alpha$$

• 定义（Poisson分布）: 参数为 $\alpha$ 的Poisson分布:$$P(X=k)=\frac{e^{-\alpha}}{k !} \alpha^k, \quad k \in N^0$$其中 $N^0={0,1,2, \cdots}$ 为非负整数集。

• 设 $X$ 是服从参数为 $\alpha$ 的Poisson分布的随机变量, 则 $\mathbb{E}(X)=\alpha$, 生成 函数为$$g(z)=\sum_{k=0}^{\infty} a_k z^k=\sum_{k=0}^{\infty} \frac{e^{-\alpha}}{k !} \alpha^k z^k=e^{-\alpha} e^{\alpha z}=e^{\alpha(z-1)}$$微分两次得$$g^{\prime}(z)=\alpha e^{\alpha(z-1)}, \quad g^{\prime \prime}(z)=\alpha^2 e^{\alpha(z-1)}$$所以$$\begin{aligned}
  E(X) & =g^{\prime}(1)=\alpha, E(X^2)=g^{\prime}(1)+g^{\prime \prime}(1)=\alpha+\alpha^2 \\
  \sigma^2(X) & =E(X^2)-E(X)^2=\alpha
  \end{aligned}$$

• 定理: 设随机变量 $X_j$ 独立, 且具有Poisson分布 $\pi\left(\alpha_j\right)$, 则 $X_1+\cdots+X_n$ 具有Poisson分布 $\pi(\alpha_1+\cdots+\alpha_n)$

• 生成函数：

  • $g(z)=e^{\alpha (z-1)}$

• 矩母函数：

  • $$M(t)=e^{α(e^t-1)} $$

• 特征函数：

  • $$\varphi(\omega)=e^{α(e^{i\omega}-1)}$$

• Poisson分布是二项式分布的极限

正态分布

• 也叫 Gauss 分布

• 密度函数为$$\varphi(x)=\frac{1}{\sqrt{2 \pi}} e^{-x^2 / 2}, \quad-\infty<x<+\infty$$的分布称为正态分布，其分布函数为$$\Phi(x):=P(X \leq x)=\int_{-\infty}^x \varphi(t) d t=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-t^2 / 2} d t$$

• 正态分布也称为Gauss分布, 或Laplace-Gauss分布, 等等。验证一下:$$\int_{-\infty}^{\infty} \varphi(x) d x=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} e^{-t^2 / 2} d t=1$$

• 密度函数的性质：

  • 偶函数，即 $\varphi(x)=\varphi(-x)$
  • 无穷可微性，各阶导数均存在
  • 总质量为1

• 力矩生成函数/矩母函数：

  • $$M(\theta)=E(e^{\theta X})=\int_{-\infty}^{\infty}e^{\theta u}\varphi(u)du=e^{\theta^2/2}$$

• 力矩：

  • $$m^{(n)}=E(X^n)=\int_{-\infty}^{\infty}u^n\varphi(u)du$$
  • $$m^{(2n-1)}=0,\quad m^{2n}=\frac{(2n)!}{2^nn!}$$

• 定义: 对任意实数 $m$ 和任意 $\sigma>0$, 称随机变量 $X$ 具有正态分 布 $N(m, \sigma^2)$, 如果变形的随机变量$$X^*=\frac{X-m}{\sigma}$$服从单位正态分布, 即具有分布函数 $\Phi$ :$$\Phi(x):=P(X^* \leq x)=\int_{-\infty}^x \varphi(t) d t=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-t^2 / 2} d t$$当 $m=0, \sigma=1$ 时， $X^*=X$ 是原来的单位正态分布。

• $X$ 的密度函数为$$\frac{1}{\sqrt{2 \pi} \sigma} \exp (-\frac{(x-m)^2}{2 \sigma^2})=\frac{1}{\sigma} \varphi(\frac{x-m}{\sigma})$$

• $X$ 的矩母函数为$$M_X(\theta)=E(e^{\theta X})=e^{m\theta + \sigma^2 \theta^2/2}$$

• 定理: 设随机变量 $X_j$ 独立, 具有正态分布 $N(m_j, \sigma_j^2)$, 则$$X_1+X_2+\cdots+X_n$$具有正态分布 $N(m_1+\cdots+m_n, \sigma_1^2+\cdots+\sigma_n^2)$

• 中心极限定理，见上

一般的正态分布

• 密度函数为$$f(x)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp (-\frac{(x-\mu)^2}{2 \sigma^2}), x \in(-\infty,+\infty)$$分布函数为$$F(x) =P(X \leq x)=\int_{-\infty}^x f(u) d u=\frac{1}{\sqrt{2 \pi \sigma^2}} \int_{-\infty}^x \exp \left(-\frac{(u-\mu)^2}{2 \sigma^2}\right) d u$$

超几何分布

• 假设一个箱子里有b个蓝色球和r个红色球， $X_n$ 表示n次抽奖中蓝色球出现的次数。

• 若抽样不放回，即每次抽出的球不放回在箱子里，$$P(X_{n}=k)=\frac{\binom{b}{k}\binom{r}{n-k}}{\binom{b+r}{n}}$$

• 此为超几何分布，其均值和方差分别为$$\mu=\frac{n b}{b+r},\quad\sigma^{2}=\frac{n b r(b+r-n)}{(b+r)^{2}(b+r-1)}$$

• 令$b+r=N$ ，蓝色球的比例为p，红色球的比例为 $q=1-p$ ，则$$p={\frac{b}{b+r}}={\frac{b}{N}},\quad q={\frac{r}{b+r}}={\frac{r}{N}}.$$于是，若抽样不放回，则$$\mathbb{P}(X_{n}=k)={\frac{\binom{Np}{k}\binom{Nq}{n-k}}{\binom{N}{n}}}$$即超几何分布，其均值和方差分别为$$\mu=n p,\quad\sigma^{2}=\frac{n p q(N-n)}{N-1}.$$当 $N\to\infty$ 我们有$$\mathbb{P},(X_{n}=,k)={\binom{n}{k}}p^{k}q^{n-k}$$以及 $$\mu=n p,\quad\sigma^{2}=n pq$$情形与放回抽样一样，即服从二项式分布

一致分布

• 随机变量 $X$ 是连续的, 取值为区间 $[a, b]$;
• 密度函数 $f$ 为分段常数:$$f(x)= \begin{cases}1 /(b-a), & a \leq x \leq b, \\ 0, & \text {其它}\end{cases}$$此分布称为一致分布（或均匀分布）。分布函数为$$F(x)=P(X \leq x)= \begin{cases}0, & x<a \\ (x-a) /(b-a), & a \leq x \leq b \\ 1, & x>b\end{cases}$$均值和方差分别为$$\mu=\frac{1}{2}(a+b), \quad \sigma^2=\frac{1}{12}(b-a)^2$$

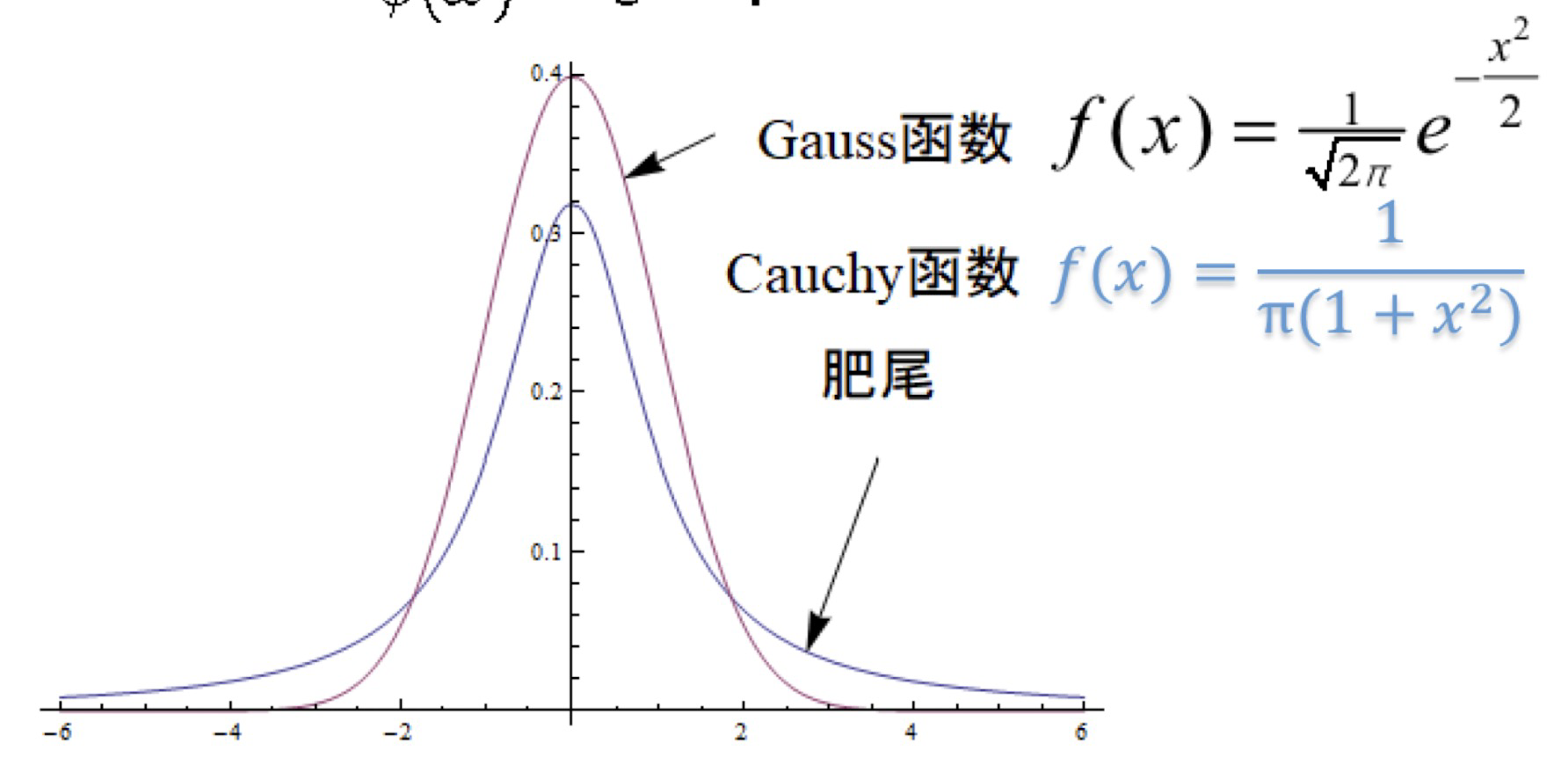
柯西分布

• 随机变量 $X$ 是连续的, 取值为区间 $(-\infty, \infty)$;
• 密度函数 $f$ 为$$f(x)=\frac{a}{\pi(x^2+a^2)}, \quad a>0, x \in(-\infty, \infty)$$此分布称为柯西分布（课堂练习题：证明它是密度函数）。但均值、方差、高阶力矩均不存在，而特征函数为$$\phi(\omega)=e^{-a \omega}$$
• 

Gamma分布

• 随机变量 $X$ 是连续的, 取值为区间 $(-\infty, \infty)$;
• 密度函数 $f$ 为一个分片函数:$$f(x)= \begin{cases}\frac{x^{\alpha-1} e^{-x / \beta}}{\beta^\alpha \Gamma(\alpha)}, & x>0 \\ 0, & x \leq 0\end{cases}$$其中 $\alpha, \beta>0, \Gamma(\alpha)$ 为微积分中的Gamma函数, 此分布称为Gamma分布.
• 均值、方差为$$\mu=\alpha \beta \quad \sigma^2=\alpha \beta^2 \text {, }$$
• 矩母函数、特征函数为$$M(t)=(1-\beta t)^{-\alpha}, \quad \phi(\omega)=(1-\beta i \omega)^{-\alpha}$$

Beta分布

• 随机变量 $X$ 是连续的, 取值为区间 $(-\infty, \infty)$;
• 密度函数 $f$ 为一个分片函数:$$f(x)= \begin{cases}\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}, & 0<x<1, \\ 0, & \text { 其它, }\end{cases}$$其中 $\alpha, \beta>0, B(\alpha, \beta)$ 为 Beta函数, 此分布称为 Beta分布。
• 均值、方差为$$\mu=\frac{\alpha}{\alpha+\beta}, \quad \sigma^2=\frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)} $$
  问：矩母函数、特征函数为什么? (课后思考题)

• （附注）Beta函数：对任何 $\alpha>0, \beta>0$,$$\begin{aligned}& B(\alpha, \beta)=\int_0^1 x^{\alpha-1}(1-x)^{\beta-1} d x \\ & B(\alpha, \beta)=\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)} \end{aligned}$$

卡方分布

• 设$X_1,X_2,\cdots,X_\nu$是$\nu$个独立单位正态分布，考虑随机变量$$\chi^{2}=X_{1}^{2}+X_{2}^{2}+\cdot\cdot\cdot+X_{\nu}^{2}$$那么，对x<0， $$\mathbb{P}\left(\chi^{2}\leq x\right)=0$$ ；对x> 0$$P(\chi^{2}\leq x)=\frac{1}{2^{\nu/2}\Gamma(\nu/2)}\int_{0}^{x}u^{\nu/2-1}{e}^{-u/2}d u$$

• 此分布称为chi方分布，p称为自由度。卡方分布可看作Gamma分布的特殊情形， $$\alpha=\nu/2,\beta=2$$故$$\mu=\nu$$$$\sigma^2=2\nu$$$$M(t)=(1-2t)^{-\nu/2}$$$$\phi(\omega)=(1-2i\omega)^{-\nu/2}$$

• 密度函数：$$F(x)=\frac{1}{2^{n/2}\Gamma(n/2)}x^{n/2-1}e^{-x/2}(x>0)$$

• 定理1: 设$X_1, X_2,\cdots,X_\nu$是$\nu$个独立单位正态分布，则随机变量 $$\chi^{2}=X_{1}^{2}+X_{2}^{2}+\cdot\cdot\cdot+,X_{\nu}^{2}$$ 服从卡方分布。

• 定理2: 设$U_1,U_2,\cdots,U_{K}$ 是k个独立卡方分布，自由度分别为$\nu_1,\nu_2,\cdots,\nu_k$, 则随机变量$W=:U_{1}+U_{2}+\cdots + U_k$是自由度为 $$\nu_{1}+\nu_{2}+\cdots+\nu_k$$ 的卡方分布。

• 定理3: 设$V_1,V_2$是两个独立分布，$V_1$是自由度为$\nu_{1}$ 的卡方分布，随机变量$V=V_{1}+V_2$是自由度为$\nu$的卡方分布,则$V_2$是自由度为$\nu-\nu_1$的卡方分布。

t分布

• 若随机变量的密度函数为$$\ell(t)={\frac{\Gamma\left({\frac{\nu+1}{2}}\right)}{\sqrt{\nu\pi}\Gamma(\nu/2)}}\left(1+{\frac{t^{2}}{\nu}}\right)^{-(\nu+1)/2},\ t\in(-\infty,\infty)$$此分布称为t分布，$\nu$称为自由度。若$\nu$很大（$\nu$ >30），该分布逼近单位正态分布。其均值、方差为$$\mu=0,\quad\sigma^{2}=\frac{\nu}{\nu-2},\left(\nu>2\right)$$
• 定理: 设Y,Z是两个独立分布，Y是单位正态分布，Z是自由度为$\nu$的卡方分布，则$$T={\frac{Y}{\sqrt{Z/\nu}}}$$是自由度为$\nu$的t分布。

几何分布

• 随机变量X表示伯努利试验直到第一次成功（等时）的次数，则$$P(X=k)=pq^{k-1},k=1,2,\cdot\cdot\cdot.$$这里p表示单一试验成功的概率。均值、方差、矩母函数如下:$$\mu=\frac{1}{p}$$$$\sigma^2=\frac{q}{p^{2}}$$$$M(t)=\frac{p e^t}{1-q e^t}$$

数理统计

抽样理论

总体（population）与样本(sample）

• 例：欲知12000名学生中的平均身高和体重？方法：随机抽取100名学生。
• 以上称为抽样。
• “总体”（population)是指研究对象的全体(如12000名学生），不可能或很难检验；有时，总体也指观察的数据，或者数据的分布，其意义要从上下文确定。
• 总体的一部分成为“样本”（如100名学生），可以检验。一方面，由于样本是从总体中随机抽取的，抽取前无法预知它们的数值，因此，样本是随机变量，用大写字母$X_1,X_2,\cdots X_n$表示；另一方面，样本在抽取以后经观测就有确定的观测值，因此，样本又是一组数值，此时也可用小写字母$x_1,x_2, \cdots X_n$，其中n表示样本的大小（称为样本容量）

随机抽样和随机数:

• 有限样本中的每个元素选取的机会一样, 称为随机抽样。
• 样本容量n也是一个随机数。

• 随机性：总体中每一个个体都有同等机会被选入样本, 即 $X_i$ 与总体 $X$ 有相同的分布。
• 独立性: 样本中每一样品的取值不影响其它样品的取值, 即随机变量 $X_1, X_2, \cdots X_n$ 是相互独立的。

以上方法称为简单随机抽样方法。所以, 我们得

• 样本 $X_1, X_2, \cdots X_n$ 可以看成是独立同分布 iid 的随机变量，其共同分布即为总体分布。
• 设总体 $X$ 具有分布函数 $F(x), X_1, X_2, \cdots X_n$ 是取自该总体的容量为 $n$ 的样本, 则样本联合分布函数为
  $$
  F\left(x_1, x_2, \cdots, x_n\right)=F\left(x_1\right) F\left(x_2\right) \cdots F\left(x_n\right)
  $$

总体参数

• 让X表示从 12000 名学生中随机抽取的学生身高, 它是一个随机变量, 对应有均值 $\mu$ 、方差 $\sigma$ 、中 位数、偏态等数量;
• 这些数量都称为总体参数。
• 若随机变量 $X$ 的概率分布或密度函数已知，则我们可知总体的信息。

样本统计量

• 在估计总体参数中, 任何从样本得来的量都称为样本统计量, 故统计量有时指随机变量, 有时指它的值。
• 样本统计量的分布称为抽样分布。

样本均值

• 样本均值
  • $${X_1, X_2, \cdots X_n}$$是来自(随机)样本中的随机变量（无特殊说明, 一般假设它们是独立、同分布的）, 则样本平均为$$\bar{X}=\frac{X_1+X_2+\cdots+X_n}{n}$$对应的样本均值为$$\bar{x}=\frac{x_1+x_2+\cdots+x_n}{n}$$
• 样本平均 $\bar{X}$ 是一个随机变量, 而样本均值 $\bar{x}$ 是对应的数值; 有时两者不加区别, 统称样本均值。

样本均值的抽样分布

• 定理1。设 $\mu$ 为总体的数学期望, 则样本平均 $\bar{X}$ 的数学期望为$$\mu_{\bar{X}}:=\mathbb{E}(\bar{X})=\mu$$即样本平均的期望值等于总体的数学期望。
• 定理2。若总体无限、抽样随机, 或者总体有限、放回抽样, 则样本平均的方差为$$\sigma^2_\bar{X}:=\operatorname{Var}(\bar{X})=\mathbb{E}[(\bar{X}-\mu)^2]=\frac{\sigma^2}{n}$$其中 $\sigma^2$ 为总体方差。
• 定理3。若总体大小为 $N$ ，抽样不放回, 样本大小为 $n \leq N$, 则样本平均的方差为$$\sigma_{\bar{X}}^2=\operatorname{Var}(\bar{X})=\frac{\sigma^2}{n} \cdot \frac{N-n}{N-1} \leq \frac{\sigma^2}{n}$$
  • 与超几何分布相关。
• 定理4。若总体服从期望为 $\mu$ 、方差为 $\sigma^2$ 的正态分布, 则随机变量 $Z:=\frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}$ 收敛单位正态分布:$$\lim_{n \rightarrow \infty} P(Z \leq x)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^xe^{-u^2/2}du$$这里假设总体无限, 或者抽样复位 （即独立同分布）。

抽样分配的差与和

• 现给定两个总体。第一、二个样本分别来自第一、二个总体, 样本容量、统计量分别为 $n_1, n_2$ 和 $S_1, S_2$, 均值和标准差（即偏差）分别为 $\mu_{S_1}, \mu_{S_2}$ 和 $\sigma_{S_1}, \sigma_{S_2}$ 。现考虑所有来自这两个总体样本的所有组合, 可得和、差$$S_1+S_2, S_1-S_2$$的分布。不难知道，若 $S_1, S_2$ 独立，则
  • $$\mu_{S_1-S_2}=\mu_{S_1}-\mu_{S_2}, \sigma_{S_1-S_2}=\sqrt{\sigma_{S_1}^2+\sigma_{S_2}^2}$$
  • $$\mu_{\bar{X}_1-\bar{X}2}=\mu_1-\mu_2, \sigma{\bar{X}_1-\bar{X}_2}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}$$

样本方差

• 样本方差:

  • 如果 $X_1, X_2, \cdots X_n$ 表示容量为 $n$ 随机样本, 则样本方差对应的随机变量定义为$$S^2=\frac{(X_1-\bar{X})^2+\cdots+(X_n-\bar{X})^2}{n}$$

• 由定理1知, $\mathbb{E}(\bar{X})=\mu$ 。当统计数据的期望值等于相应总体参数的期望值, 我们称统计数据为无偏差, 该值为该参数的无偏估计 （unbiased estimate）。

• 定理5：设总体方差为 $\sigma^2$, 则$$\mu_{S^2}:=\mathbb{E}\left(S^2\right)=\frac{n-1}{n} \sigma^2$$（该值收敛 $\sigma^2$, 当 $n \rightarrow \infty$ ）

• 因为$$\mu_{S^2}-\sigma^2=\frac{n-1}{n} \sigma^2-\sigma^2 \neq 0$$$S^2$ 与总体有偏差。理想的无偏估计要乘一个因子，即定义为$$\widehat{S}^2=\frac{n}{n-1} S^2=\frac{(X_1-\bar{X})^2+\cdots+(X_n-\bar{X})^2}{n-1}$$

• 于是, 当在总体无限或有限总体而放回抽样的情况下,$$\mathbb{E}(\widehat{S}^2)=\frac{n}{n-1} \mathbb{E}(S^2)=\frac{n}{n-1} \cdot \frac{n-1}{n} \sigma^2=\sigma^2$$

• 即 $\widehat{S}^2$ 为一个无偏统计量。

• 对不放回抽样的有限总体，则有$$\mathbb{E}(S^2)=(\frac{N}{N-1})(\frac{n-1}{n}) \sigma^2$$

样本方差的抽样分布

• 考虑所有容量为 $n$ 的随机样本, 然后计算每个样本的方差, 此方差也是一个随机变量, 于是我们可以得到该方差 （随机变量） 的抽样分布。与计算 $\widehat{S}^2$ 或 $S^2$ 的抽样分布相比, 有时较易计算下列随机变量的抽样分布:$$V=\frac{n S^2}{\sigma^2}=\frac{(n-1) \widehat{S}^2}{\sigma^2}=\frac{(X_1-\bar{X})^2+\cdots+(X_n-\bar{X})^2}{\sigma^2}$$
• 定理6。设随机样本的容量为 $n$, 对应的总体服从方差为 $\sigma^2$ 正态分布, 则随机变量V服从自由度为 $n-1$ 的卡方分布。

总体均值的估计

• 若总体服从正态分布 $N\left(\mu, \sigma^2\right)$, 则正规化的随机变量$$Z=\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}$$服从单位正态分布 $N(0,1)$ 。

• 一般地（总体不一定服从正态分布）, 根据中心极限定理, 只要满足独立、同分布, 该随机变量总是收敛到单位正态分布(如 $n \geq 30$ )。若总体方差 $\sigma$ 已知, Z可以用来估计总体的均值。

  • 若总体方差末知怎么办? 一种可能性是使用样本方差 （$S$ 或 $\widehat{S}$, 均是一个随机变量）, 然后利用Z来估计总体均值。

• 定理7: 设随机样本容量为 $n$ 、总体服从均值为 $\mu$ 的正态分布, 则$$T=\frac{\bar{X}-\mu}{\widehat{S} / \sqrt{n}}=\frac{\bar{X}-\mu}{S / \sqrt{n-1}}$$服从自由度为 $v=n-1$ 的 $\mathbf{t}$ 分布, 即密度函数为$$f(t) =\frac{\Gamma(\frac{v+1}{2})}{\sqrt{v \pi} \Gamma(v / 2)}(1+\frac{t^2}{v})^{-(v+1) / 2}=\frac{1}{\sqrt{v} B(\frac{1}{2}, \frac{v}{2})}(1+\frac{t^2}{v})^{-\frac{1}{2}-\frac{v}{2}}, t \in(-\infty, \infty)$$这里用到 $B\left(\frac{1}{2}, \frac{v}{2}\right)=\frac{\Gamma\left(\frac{1}{2}\right) \Gamma\left(\frac{v}{2}\right)}{\Gamma\left(\frac{(1+v}{2}\right)}=\frac{\sqrt{\pi} \Gamma\left(\frac{v}{2}\right)}{\Gamma\left(\frac{1+v}{2}\right)}$ 。

• 注：t-分布用于估计“样本较小、方差末知、总体服从正态分布”的均值

分组数据

• 
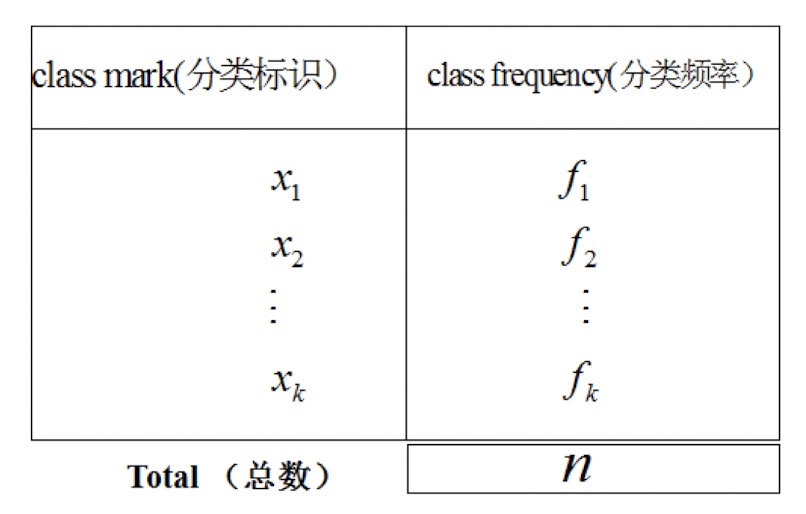
• $n=f_1+f_2+\cdots+f_k$
• 既然有 $f_1$ 个元素取值为 $x_1$, 有 $f_2$ 个元素取值为 $x_2$, 等等, 则均值为$$\bar{x}=\frac{f_1 x_1+f_2 x_2+\cdots+f_k x_k}{n}=\frac{\sum f x}{n}$$
• 方差为$$s^2=\frac{f_1(x_1-\bar{x})^2+f_2(x_2-\bar{x})^2+\cdots+f_k(x_k-\bar{x})^2}{n}$$
• 关于均值的r阶力矩为$$m_r=\frac{f_1(x_1-\bar{x})^r+\cdots+f_k(x_k-\bar{x})^r}{n}=\frac{\sum f(x-\bar{x})^r}{n}$$
• 关于原点的r阶力矩为$$m_r^{\prime}=\frac{f_1 x_1^r+\cdots+f_k x_k^r}{n}=\frac{\sum fx^r}{n}$$

估计理论

1. 无偏估计和有效估计

• 定义：若一个统计量的数学期望等于总体的数学期望, 则称该统计量为总体参数的无偏估计量, 对应的统计值称为无偏估计值 （unbiased estimate）
• 如果两个统计量的抽样分布有相同的数学期望（或均值）, 具有较小方差的统计量称为更有效的均值估计量, 相应的值称为有效估计（efficient estimate）

2. 点估计，区间估计和可靠性

• 由单一数量所决定的总体参数估计, 称为参数的点估计。
• 由两个数量构成的区间、且认为该参数位于该区间的 （总体参数） 估计，称为参数的区间估计。
• 例如：如果说距离是5.28米, 这就是点估计; 如果我们说距离 是 $5.280 \pm 0.03$ 米, 即距离位于5.25和5.31米之间, 这就是一个区间估计。
• 一个估计的误差或精度称为其可靠性。

置信区间

• 置信区间是总体参数的一种区间估计, 用来衡量估计的可靠性;
• 它的计算来自观察数据，不同的抽样有不同的置信区间。 置信水平表明抽样所得的置信区间反应真正总体参数的概率, 通常用百分比表示, 如 “我们 $99 %$ 相信参数真值在置信区间中”
• 置信水平越大，置信区间越大，从而参数估计越不精确。

情况1

• 第一种情况是 $\sigma$ 已知。 此时, 枢轴量为$$T=\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}$$它服从单位正态分布;
• 例：
  • 假设随机变量X服从均值为250（理想值，未知） 、偏差为 $\sigma=2.5$ 的正态分布, 即 $X \sim N\left(250,2.5^2\right)$ 。随机抽样 $n=25$ ，发现数值分别为 $X_1, \cdots, X_{25}$, 均值为$$\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i=250.2$$
  • 如果取另外一个抽样, 可以想象均值有变化。
  • 围绕观察值250.2, 有一个样品均值 $\mu$ 区间, 使得观察数据不会出现异常, 此区间称为 $\mu$ 的置信区间。
  • 具体问： $\mu$ 的值在 $95 %$ 的情况下位于什么区间?
• 解：
  • 第一步，推导数学公式：$Z=\frac{\bar{X}-\mu}{\sigma / \sqrt{n}}=\frac{\bar{X}-\mu}{0.5} \quad$ （称为枢轴量）服从单位正态分布 $N(0,1)$ 。从而, 可能找出不依赖 $\mu$ 数 值 $-z$ 和 $z$, 使得随机变量 $Z$ 在 $-z$ 和 $z$ 之间的概率 为 $1-\alpha=0.95$, 即$P(-z \leq Z \leq z)=1-\alpha=0.95$
  • 第二步，简化计算：分布函数 $\Phi$ 为$$\Phi(z)=P(Z \leq z)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^z e^{-\frac{u^2}{2}} d u$$所以,$\Phi(z)=1-\frac{\alpha}{2}=1-\frac{1-0.95}{2}=0.975$
  • 第三步，计算区间端点：已知 $\Phi(z)=0.975$, 从单位正态分布表查得$0.975=\Phi(1.96)$，所以, $z=1.96$, 即$$\begin{aligned}0.95 & =1-\alpha=P(-z \leq Z \leq z) \\ & =P(-1.96 \leq \frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \leq 1.96) \\ & =P(\bar{X}-1.96 \frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X}+1.96 \frac{\sigma}{\sqrt{n}})\end{aligned}$$已知 $\sigma=2.5, n=25$, 则$$1.96 \times \frac{\sigma}{\sqrt{n}}=1.96 \times 0.5=0.98$$
  • 因此,$$0.95=P(\bar{X}-0.98 \leq \mu \leq \bar{X}+0.98)$$
  • 解释如下：参数 $\mu$ 介于随机端点 $\bar{X}-0.98$ 和 $\bar{X}+0.98$ 之间的概率 为 0.95 。 注意, 此处 $\bar{X}$ 来自观测数据, 不同的人可能得到不同的数据。我们得数据是 $\bar{X}=250.2$ ，从而我们的置信区间为$$(250.2-0.98,250.2+0.98)=(249.22,251.18)$$
  • 换言之, 可以说 $\mu$ 的值在 $95 %$ 的情况下位于上述区间, 不在上述区间的情况只有 $5 %$ 。由于 $\mu$ 的理想值是 250 , 没有理由说自动售货机不正常。解毕。

情况2

• 第二种情况是 $\widehat{S}$ 已知 （ $\sigma$ 末知） 。此时, 枢轴量为$$T=\frac{\bar{X}-\mu}{\widehat{S} / \sqrt{n}}$$它服从自由度为 $\nu=n-1$ $t$ 分布（即第一种情况的 $\sigma$ 变为 $\widehat{S}$ ，单位正态分布变 为 $t$ 分布）。
• 例：
  • 经抽样, 我们得到数据$$n=12, \bar{X}=4.7092, \widehat{S}^2=0.0615$$求 $\mu$ 的$95%$置信区间。（此处 $\sigma$ 未知）
• 解：
  • 已建立数学公式 （即已知枢轴量）。设 $F_\nu(t)=P(T \leq t)$ 为 分布函数, $\nu=12-1=11$ 。
  • 第一步（求临界值）:利用对称性 $F_\nu(-c)=1-F_\nu(c)$, $F_\nu(c)-F_\nu(-c)=P(-c \leq T \leq c)=0.95=p$ 即 $F_\nu(c)=\frac{1+p}{2}=0.975$, 从而 $c=2.20$ （查表）.
  • 第二步（求置信区间）:计算$$\frac{c \widehat{S}}{\sqrt{n}}=2.20 \times \sqrt{\frac{0.0615}{12}}=0.157$$所求置信区间为$$\begin{aligned}& (\bar{X}-\frac{c \widehat{S}}{\sqrt{n}}, \bar{X}+\frac{c \widehat{S}}{\sqrt{n}})=(4.7092-0.157,4.7092+0.157) \\ & =(4.552,4.866) . \quad(\text { 比较 } \bar{X}=4.7092 \text { 的值 }) \text { 解毕。 }\end{aligned}$$

$\sigma^2$ 置信区间

• $\mu$ 末知时， 如何求方差 $\sigma^2$ 的 $1-\alpha$ 置信区间?
• 方法：第一步（求临界值）：注意随机变量$$T=\frac{(n-1) \widehat{S}^2}{\sigma^2} \sim \chi^2(n-1)$$即枢轴量 $T$ 服从卡方分布。但卡方分布是偏态分布, 分布函数的图像不对称。回忆 $\chi^2(k)$ 的密度函数 $f_k$ 为$$f_k(x)=\frac{1}{2^{k / 2} \Gamma(k / 2)} x^{k / 2-1} e^{-x / 2}, \quad x>0$$通常寻找等尾置信区间, 即将分布函数图像两侧面积分别取为 $\frac{\alpha}{2}$, 中间剩余面积为 $1-\alpha$ 。记分布函数为 $F_{n-1}(x)$, 令$$\begin{aligned}\frac{\alpha}{2} & =F_{n-1}(x_1)=\int_0^{x_1} f_{n-1}(x) d x, \\ 1-\frac{\alpha}{2} & =F_{n-1}(x_2)=\int_0^{x_2} f_{n-1}(x) d x\end{aligned}$$既然 $\alpha$ 已知, 查表可知 $x_1, x_2$ 的值。
• 第二步（求区间端点）：于是,$$P(x_1 \leq \frac{(n-1) \widehat{S}^2}{\sigma^2} \leq x_2)=1-\alpha$$所以 $\sigma^2$ 的 $1-\alpha$ 置信区间为$$(\frac{(n-1) \widehat{S}^2}{x_2}, \frac{(n-1) \widehat{S}^2}{x_1})$$再开方, 可得 $\sigma$ 的 $1-\alpha$ 置信区间$$(\widehat{S} \sqrt{\frac{(n-1)}{x_2}}, \widehat{S} \sqrt{\frac{(n-1)}{x_1}})$$解毕。

3. 极大似然估计

• 虽然置信区间在总体参数估计中很重要，但有时单个估计或点估计更方便。为了获得一个“最佳”估计，我们采用最大似然法或“费舍尔”方法。该方法如下：设总体具有密度函数，带参数 $\theta$, 表示为 $f(x, \theta)$ 。假设有 $n$ 个独立观测 $X_1, \cdots, X_n$, 联合密度函数为$$L=f(x_1, \theta) f(x_2, \theta) \cdots f(x_n, \theta)$$称为“似然”。令导数 $\frac{d L}{d \theta}=0$ （两边取对数再求导），故$$\frac{1}{f(x_1, \theta)} \frac{\partial f(x_1, \theta)}{\partial \theta}+\frac{1}{f(x_2, \theta)} \frac{\partial f(x_2, \theta)}{\partial \theta}+\cdots+\frac{1}{f(x_n, \theta)} \frac{\partial f(x_n, \theta)}{\partial \theta}=0$$其解 $\theta=\theta(x_1, \cdots, x_n)$ 称为 $\theta$ 的极大似然估计量。
• 例题: 设总体服从方差已知、但均值末知的正态分布, $X_1, \cdots, X_n$ 为 $n$ 个观测量, 求均值的极大似然估计。
• 解：
  • 密度函数$$f(x_k, \mu)=\frac{1}{\sqrt{2 \pi \sigma^2}} e^{-(x_k-\mu)^2 /(2 \sigma^2)}$$从而我们得$$\begin{aligned} & L=f(x_1, \mu) \cdots f(x_n, \mu)=(2 \pi \sigma^2)^{-n / 2} e^{-\sum_{k=1}^n(x_k-\mu)^2 /(2 \sigma^2)}, \\ \Rightarrow & \ln L=-\frac{n}{2} \ln (2 \pi \sigma^2)-\frac{1}{2 \sigma^2} \sum(x_k-\mu)^2 \\ \Rightarrow & \frac{1}{L} \frac{\partial L}{\partial \mu}=\frac{1}{\sigma^2} \sum(x_k-\mu)\end{aligned}$$
  • 令 $\frac{\partial L}{\partial \mu}=0$ 得，$$\mu=\frac{\sum x_k}{n}$$即均值的极大似然估计就是样品均值。

4. 贝叶斯估计