Ch1 Introductory
what is econometrics
- Combine statistical techniques with economic theory.
- Estimating economic relationships.
- testing economic theories.
- evaluating and implementing government and business policy.
basic types
Descriptive
- challenges
- Sampling
- draw conclosion about the population based on sample.
- Summary statistics
- nice way to summarize complicated data.
- Sampling
- If we have data we would know the answer.
- Conditional Expectations: if I condition X to be some value, what is the expect value of Y. Often a variable that can take on a very large number of values is treated as continuous for convenient.
- Example
- Mothers smoke one more cigarette during pregnancy are expected to give birth to child with 15g lower birth weight.
Forecasting
- challenges
- Underfitting
- Overfitting
- If we know the data and wait long enough, we will know the answer.
Causal (for structural)
- Correlation: how two random variables move together
- The difference between causation and correlation is a key concept in econometrics. We would like to identify causal effects and estimate their magnitude.
- It is generally agreed that this is very difficult to do; having an economic model is often essential in establishing the causal interpretation.
- Unless run perfect experiment, we will never know the answer.
- requires $𝐸(𝑢|𝑥) = 0$
- Econometrics focus on causal problems inherent in collecting and analyzing observational economic data.
- 有几种可能:
- x -> y
- z -> x, z -> y
- y -> x
- Example
- Mothers smoke one more cigarette during pregnancy causes their child to have 15g lower birth weight.
Structure of Economic data
Cross-sectional data
- A cross-sectional data set consists of a sample of units taken at a given point in time.
- 截面数据
- assume:
- sample is drawn from the underlying population randomly
- Violation of random sampling: We want to obtain a random sample of family income. However, wealthier families are more likely to refuse to report.
Time-Series data
- Each observation is uniquely determined by time
- 时间序列
- A time series data set consists of observations on a variable or several variables over time.
- 可以是对多个变量的时间序列
- Time is an important dimension in a time series data set.
Pooled Cross Sections and Panel or Longitudinal Data
- Pooled cross sections include cross-sectional data in multiple years.
- A panel data set consists of a time series for each cross-sectional member in the data set.
- Panel data:
- the same units over time
- pooled cross sections:
- diferent units, diferent time.
- Each observation is uniquely determined by the unit and the time.
- 同时具备时间和变量差异
Ch2 The Simple Regression Model:
Interpretation and Estimation
Descriptive analysis
- Define conditional expectation E(y|x)
- if I condition X to be some value, what is the expected value of Y?
Simple Linear model
$$E(y|x)=\beta_0+\beta_1x$$
$$\beta_0=E(y|x=0)$$
$$\beta_1=\frac{\partial E(y|x)}{\partial x}$$
let $u=y-E(y|x)$, thus $E(u|x)=0$
$$\hat{u_i}=y_i-\hat{\beta_0}-\hat{\beta_1}x_i$$
using law of iterated expectation, we get
- $E(u)=0$, and $E(ux)=0$
对于总体,写成 $y_i=\beta_0+\beta_1x_i+u_i$
对于样本,写成 $y_i=\hat{\beta_0}+\hat{\beta_1}x_i+\hat{u_i}$
- 带帽子表示的是样本,用来估计实际值
Method of Moments
Method of moments: use the sample average to estimate the population expectation
Use $\frac{1}{N}\sum$ to replace $E[·]$
population expectations sample analogue $E(u)=0$ $\frac{1}{N}\sum \hat{u_i}=0$ $E(ux)=0$ $\frac{1}{N}\sum x_i\hat{u_i}=0$ using $\hat{u_i}=y_i-\hat{\beta_0}-\hat{\beta_1}x_i$ to represent u, the result is :
- $$\hat{\beta_1}=\frac{\frac{1}{N}\sum_{i=1}^N(x_i-\bar{x})(y_i-\bar{y})}{\frac{1}{N}\sum_{i=1}^N(x_i-\bar{x})^2}$$
- $$\hat{\beta_0}=\bar{y}-\hat{\beta_1}\bar{x}$$
Causal Estimation
- $$y=\beta_0+\beta_1 x+u$$
- $\beta_{0}$ and $\beta_1$ are unknown numbers in the nature we want to uncover
- You choose x
- Nature chose u in a way that is unrelated to your choice of x
- u represent things affect y other than x
- we think of u as some real thing, It’s just we can’t observe it
- u 是一个实际存在的变量
- To estimate the model,we need to know how u is determined.
- The simplest case is that u is assigned at random
- We can write this as $E(u|x)=0$.
- u 不随着 x 而变
- 重要!协方差为0
- 均值是0
- u 不随着 x 而变
- 对于上式两边取期望,对x求偏导:
- $$\frac{\partial E[y|x]}{\partial x}=\beta_{1}+\frac{\partial E[u|x]}{\partial x}$$
- 只有当$E[u|x]$ 是常数时,$\beta_1$ 表示当x变化1时,y的平均变化。
- This condition gives the model a causal interpretation:
- if $E(u|x)$ does not vary when x changes, then any change in y can be attributed to x
- 因此$\beta_{1}$ 反应了x对y的因果关系
Forecasting
- 我们希望得到:
- $$\hat{y}^*=\hat{\beta_0}+\hat{\beta_1}x^*$$
- 和causal不同,因为我们没有自己选择 $x^*$
- 使用最小二乘法,argmax来判断回归的y和真实值的关系。
两种方法:moment和OLS
Properties of Simple Regression Model
Properties of OLS on Any Sample of Data
$$\sum_{i=1}^{N}\hat{u}_{i}=0.$$
$$\sum_{i=1}^{N}x_{i}{\hat{u}}_{i}=0.$$
$$\sum_{i=1}^N\hat{y}_i\hat{u}_i=0$$
$$\hat{\beta_0}+\hat{\beta_1}\bar{x}=\bar{y}$$
Goodness of Fit
- measure how well our model fits the data
- decompose $y_i$ into two parts: the fitted value and the residual.
- $$y_i=\hat{y_i}+\hat{u_i}$$
- 第一部分是模型解释的,第二部分不是
- Define the following terms:
Total sum of squares(SST)$$S S T=\sum_{i=1}^{N}\bigl(y_{i}-\bar{y}\bigr)^{2}.$$
Explained sum of squares(SSE)$$S S E=\sum_{i=1}^{N}({\hat{y}}_{i}-{\bar{y}})^{2}.$$
Residual sum of squares(SSR)$$S S R=\sum_{i=1}^{N}\hat{u}_{i}^{2}.$$
$$SST=SSE+SSR$$
- 定义 Goodness of fit, $R^2$
- $$R^2=\frac{SSE}{SST}$$
- 即y有多大的部分是由$y_i$ 解释的
- 总是在0到1之间
- 只是描述了x和y的相关性,并不能表示因果关系
Functional form
$$log(y)=\beta_0+\beta_1 x+u$$
- $$\beta_1=\frac{dlog(y)}{dy}=\frac{dy}{y}\cdot\frac{1}{x}$$

Expected Values and Variances of the OLS Estimators
Unbiasedness of OLS
- Unbiasedness means the expectation of the estimator equals the true value.
- 无偏性
- $E(\hat{\beta})=\beta$
假设:SLR(simple linear regression)
- Linear in Parameters
- Random Sampling
- $Cov(u_i,u_j)=0$
- Sample Variation in the Explanatory Variable
- 即自变量x的取值不能只有一个点
- Zero Conditional Mean: $E(u|x) = 0$
在上面四个条件成立时,$\beta_0$ 和 $\beta_1$ 都满足无偏性
- Though the OLS estimator is unbiased, it is still possible that the estimates calculated using the sample is very different from β in the population.
- Homoskedasticity
- The error u has the same variance given any value of the explanatory variable.
- In other words, $Var(u|x)=\sigma^2$
- 同方差性
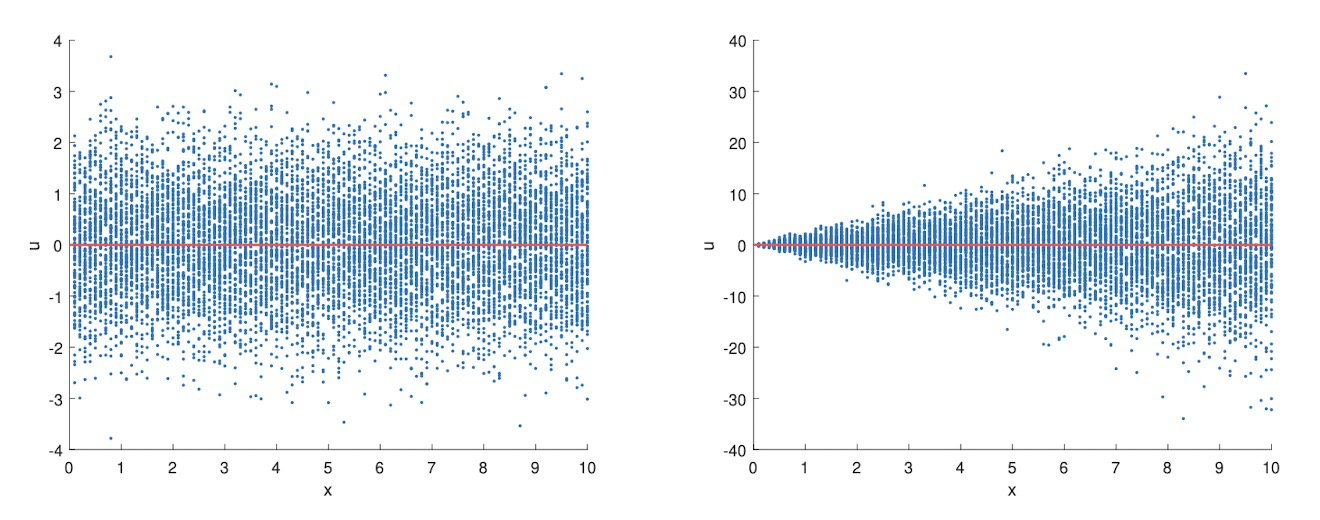
在上面5个条件成立时,可以求方差:
- $$Var(\hat{\beta_1}|x)=\frac{\sigma^2}{\sum_{i=1}^N(x_i-\bar{x})^2}=\frac{\sigma^2}{SST_x}$$
- 其中 $\sigma$ 是 u 的标准差
- 当 $\sigma$ 大时$V a r(\hat{\beta}_{1}|x)$ 方差大
- 当 x 的方差大时 $V a r(\hat{\beta}_{1}|x)$ 小
- $$V a r(\hat{\beta_0}|x)=\frac{\sigma^2\sum_{i=1}^Nx_i^2}{N\sum_{i=1}^N(x_i-\bar{x})^2}$$
估计$\sigma$
- 需要用sample来估计 $\sigma^2$
- $$s^2\equiv\hat{\sigma}^2=\frac{1}{N-2}\sum_{i=1}^N\hat{u}_i^2$$
- 这是无偏估计,其中-2是因为有两个约束条件,少了两个自由度。
Ch3 Multiple Regression Analysis: Estimation
Why we need multiple regression model?
- Descriptive analysis: sometimes we want to estimate the conditional mean of y on multiple variables
- Causal estimation: we know that something other than x may afect y, so we explicitly control them.
- Forecasting: we want to use more variables to better predict y
Estimation and Interpretation
- Population regression model:$$y=\beta_0+\beta_1 x_1+\cdots+\beta_nx_n+u$$
- zero conditional mean:
- $$E(u|x_1,\cdots,x_n)=0$$
- besides, using law of iterated expectation
- $$E(x_ju)=0\quad E(u)=0$$
- zero conditional mean:
- Fitted value: $$\hat{y_i}=\hat{\beta_0}+\hat{\beta_1}x_{i1}+\cdots+\hat{\beta_k}x_{i k}$$
- residual: $$\hat{u_i}= y_{i}-\hat{y_i}$$
Sample analog
| population expectations | sample analogue |
|---|---|
| $E(u)=0$ | $\frac{1}{N}\sum \hat{u_i}=0$ |
| $E(x_1u)=0$ | $\frac{1}{N}\sum x_{i1}\hat{u_i}=0$ |
| $E(x_ku)=0$ | $\frac{1}{N}\sum x_{ik}\hat{u_i}=0$ |
OLS
- $$H\equiv\sum_{i=1}^n\hat{u_i}^2=\sum(y_i-b_0-b_1x_{i1}-\cdots-b_kx_{i k})^2$$
- 求最小值,得一阶条件:
- $$\frac{\partial H}{\partial b_0}=-\sum_{i=1}^n2(y_i-\hat{\beta_0}-\hat{\beta_1}x_{i1}-\cdots-\hat{\beta_k}x_{ik})=0$$
- $${\frac{\partial H}{\partial b_{j}}}=-\sum_{i=1}^{n}2x_{i j}(y_{i}-{\hat{\beta_0}}-{\hat{\beta_1}}x_{i1}-\cdots-{\hat{\beta_k}}x_{i k})=0,\forall j=1,2,…,k.$$
- OLS and sample analogue give the same answer.
Interpretation
The coeicient of $x_i$ represents holding fixed other factors, the change in y when $x_i$ increases by one unit.
$$\Delta\hat{y}=\hat{\beta}_1 \Delta x_1+\hat{\beta}_2 \Delta x_2+\cdots+\hat{\beta}_k \Delta x_k$$
求 $\hat{\beta_j}$: Frisch-Waugh-Lovell Theorem
- Regress $x_j$ on other independent variables (including the constant), obtain the residual $\hat{r_{ij}}$.
- Regress y on other independent variables (including the constant), obtain the residual $\hat{r_{iy}}$.
- Regress $\hat{r_{iy}}$ on $\hat{r_{ij}}$, The resulting slope coefficient is $\hat{\beta_j}$
Goodness of fit
- 和 SLR 相同
- 但随着变量增加 $R^2$ 几乎一定会增大
- 引入 Adjusted R2
- $$\bar{R}^2=1-\frac{SSR/(N-k-1)}{SST/N-1}=1-(1-R^2)\frac{N-1}{N-k-1}$$
- N represents the size of the sample, k represents the number of independent variables (excluding the constant)
Expected Values and Variances of the OLS Estimators
假设:MLR(multiple linear regression)
- Linear in Parameters
- Random Sampling
- $Cov(u_i,u_j)=0$
- No perfect collinearity
- 不能线性相关
- 不然无法区别这些线性相关成分
- Zero Conditional Mean:
- $E(u|x_1,\cdots,x_k) = 0$
- 在上面四个条件成立时,$\beta_0$ 和 $\beta_1$ 都满足无偏性
- Homoskedasticity
- $Var(u|x_1,\cdots,x_k)=\sigma^2$
- 同方差性
MLR1-5合成 Gauss-Markov Assumption
在Gauss-Markov条件下,方差满足:
- $$V a r(\hat{\beta_j})=\frac{\sigma^{2}}{SST_j(1-R_j^2)}$$
- $R_j^2$ is the R-squared from regressing $x_j$ on all other independent variables and including an intercept
The unbiased estimator of $σ^2$ is:
- $$\hat{\sigma}^{2}=\frac{1}{N-k-1}\sum_{i=1}^{n}\hat{u}_{i}^{2}.$$
- 自由度:N-k-1
- 是无偏估计
BLUE
| sdandard deviation | standard error |
|---|---|
| $sd(\hat{\beta_j})$ | $se(\hat{\beta_j})$ |
| $\frac{\sigma}{[SST_j(1-R_j^2)]^{1/2}}$ | $\frac{\hat{\sigma}}{[SST_j(1-R_j^2)]^{1/2}}$ |
| $\sigma^2=\text{Var of u}$ | $\hat{\sigma}^{2}=\frac{1}{n-k-1}\sum \hat{u}^2$ |
| unknown | estimated using sample |
- OLS 是 best linear unbiased estimator, BLUE
- 满足线性,并且方差最小。
Practical issues
Omitted bias
假设有两个自变量,但只对其中一个进行回归,那么得到的$\hat{\beta}$ 与实际值有一个误差。
$E(\tilde{\beta}_1)=\beta_1+\beta_2\tilde{\delta}_1$
thus, $Bias(\tilde{\beta_1})=\beta_{2}\tilde{\delta}_{1}$
$Corr(x_1,x_2)>0$ $Corr(x_1,x_2)<0$ $\beta_2>0$ Positive Bias Negative Bias $\beta_2<0$ Negative Bias Positive Bias 影响无偏性
including irrelavent
- 不影响无偏性,但方差会变大
Multicollinearity
- high (but not perfect) correlation between two or more independent variables
- 不影响无偏性,但方差会变大
Ch4 Multiple Regression Analysis: Inference
Classical Linear Regression Model
The Distribution of $\hat{β_j}$
为了得到分布,在Gauss-Markov条件上还要加上一条:
MLR6: Normality
- $$u\sim N(0,\sigma^2)$$
Assumptions MLR.1 through MLR.6 are called the classical linear model CLM assumptions.
summarize the population assumptions of the CLM is
- $$y|{\bf x}\ \sim\ No r m a l(\beta_{0}\ +\beta_{1}x_{1}+\ldots+\beta_{k}x_{k},\sigma^{2})$$
在CLM条件下,$\beta$ 服从正态分布
- $$\frac{\hat{\beta}_j-\beta_j}{sd(\hat{\beta}_j)}\sim Normal(0,1)$$
但由于实际中标准差不知道,需要用标准误来算。
- $$\frac{\hat{\beta_j}-\beta_j}{s e(\hat{\beta_j})}\sim t_{N-k-1}= t_{d f},$$
- 服从t分布,N-k-1是自由度,N是多少个样本,k是回归里面有多少个x
t检验
- 检验某个系数是否为0
Null hypothesis
- Let $H_0$ be the null hypothesis that we want to test. Let $H_1$ be the alternative hypothesis.
- We reject the null hypothesis when the test statistic falls in the rejection region.
rejection region
- type 1 error:
- significance level = α = $Pr(\text{rejecting }H_0|H_0\text{ is true})$
- type 2 error:
- $Pr(\text{not rejecting }H_0|H_1\text{ is true})$
- 我们的想法是先固定一个significance level,确定对type 1 error 的容忍度,然后再最小化 type 2 error
Testing Against One-Sided Alternatives
- Suppose we are interested in testing
$$
\begin{array}{ll}
H_0: & \beta_j=0 . \\
H_1: & \beta_j>0 .
\end{array}
$$ - Consider a test statistic:$$\frac{\hat{\beta}_j-\beta_j}{\operatorname{se(}(\hat{\beta}_j)}$$
- When $H_0$ is true, the test statistic is: $$\frac{\hat{\beta_j}}{s e(\hat{\beta_j})} \sim t_{N-k-1}=t_{df}$$
- It depends on the data.
- We know its distribution under $H_0$.
- 令 $$t_{\hat{\beta}_j} \equiv \frac{\hat{\beta}_j}{s e(\hat{\beta}_j)}$$
- We often call $t_{\hat{\beta}_j}$ t-statistic or t-ratio of $\hat{\beta}_j$.
- $t_{\hat{\beta}_j}$ has the same sign as $\hat{\beta}_j$, because $\operatorname{se}(\hat{\beta}_j)>0$.
- 直觉上, 当 $t_\hat{\beta_j}$ 足够大的时候拒绝 $H_0$ : $t_\hat{\beta_i}$ 越大, $H_0$ 是真的可能性越低, $H_1$ 是真的可能性越高。
- 多大算足够大?
- Fix a significance level of $5 %$. The critical value, $c$ is the 95 th percentile when $H_0$ is true. It means when $H_0$ is true, the probability of getting a value as large as $c$ is $5 %$.
- Rejection rule:$t_{\hat{\beta}_j}>c$
- Rejecting $H_0$ when $t_{\hat{\beta}_j}>c$ means the probability of making a type I error, that is, the probability of rejecting $H_0$ when $H_0$ is true, is $5 %$.
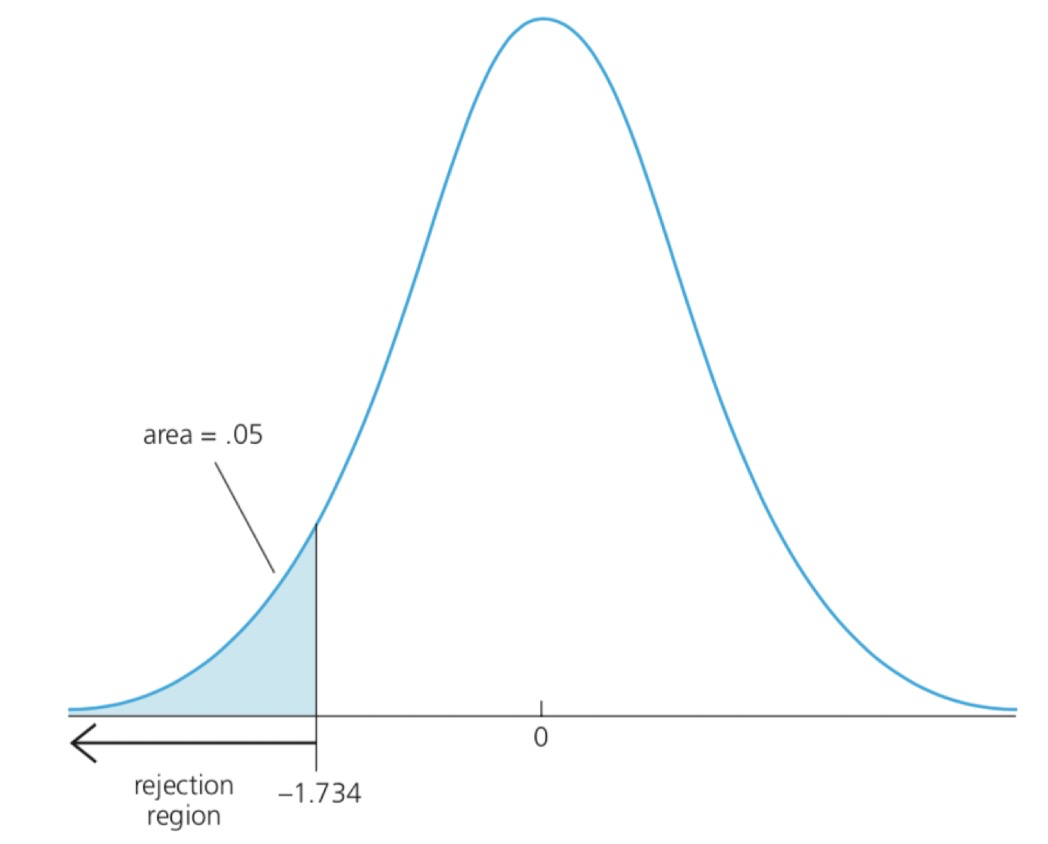
The idea of test
- Fix a significance level $\alpha$. That is, decide our level of “tolerence” for the type I error.
- Find the critical value associated with $\alpha$. For $H_1: \beta_j>0$, this means finding the $(1-\alpha)$-th percentile of the $\mathrm{t}$ distribution with $d f=N-k-1$.
- Reject $H_0$ if $t_{\hat{\beta}_j}>c$
- 通常第一类错误和第二类错误是不能同时缩小的。需要取舍。
Two-sided Alternatives
We want to test:$$\begin{array}{ll}H_0: & \beta_j=0 . \\ H_1: & \beta_j \neq 0 .
\end{array}$$This is the relevant alternative when the sign of $\beta_j$ is not well determined by theory.
Even when we know whether $\beta_j$ is positive or negative under the alternative, a two-sided test is often prudent.
求法:
- Fix a significance level $\alpha$. That is, decide our level of “tolerence” for the type I error.
- Find the critical value associated with $\alpha$. For $H_1: \beta_j \neq 0$, this means finding the $(1-\alpha / 2)$-th percentile of the $\mathrm{t}$ distribution with $d f=N-k-1$.
- Reject $H_0$ if$$|t_{\hat{\beta}_j}|>c .$$
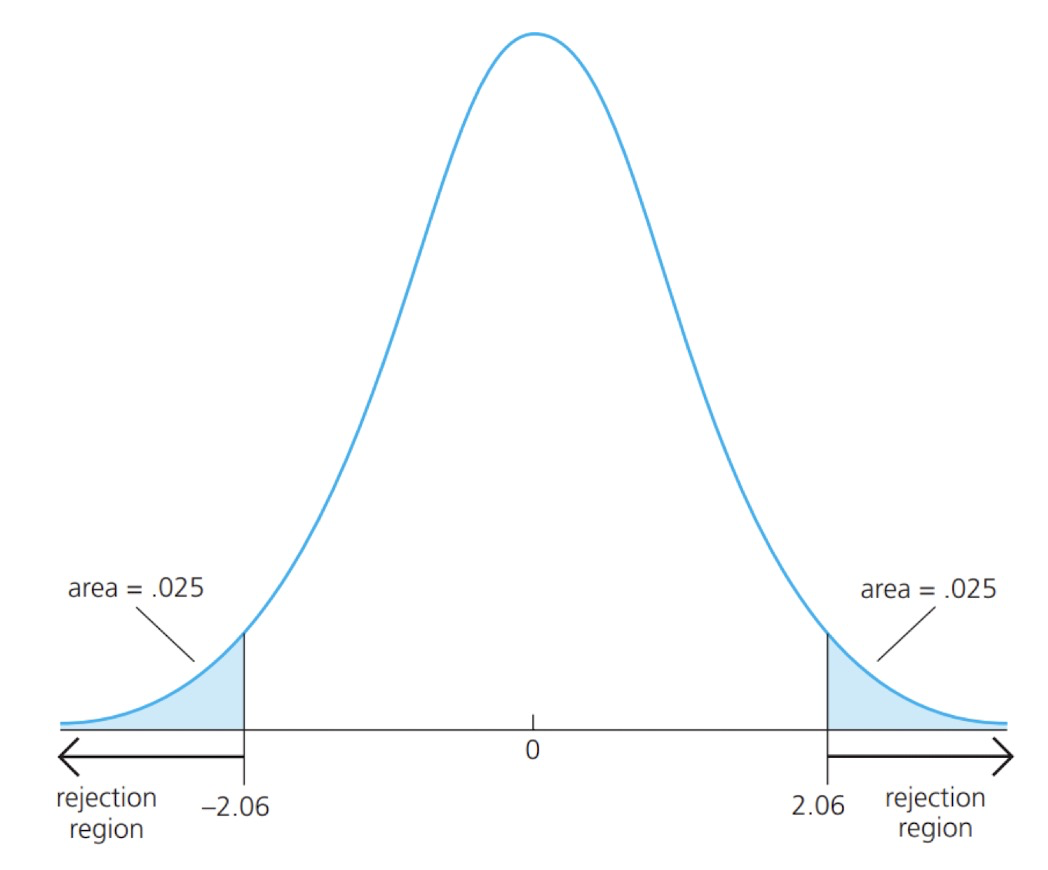
没有说明的话通常是双边的
If $H_0$ is rejected in favor of $H_1: \quad \beta_j \neq 0$ at the $5 %$ level, we usually say that “ $x_j$ is statistically significant, or statistically different from zero, at the $5 %$ level.”
If $H_0$ is not rejected, we say that “ $x_j$ is statistically insignificant at the $5 %$ level.”
Other Hypothesis
- If the null is stated as:
$$
H_0: \beta_j=a_j
$$
Then the t-statistic is$$\frac{\hat{\beta_j}-a_j}{\operatorname{se}(\hat{\beta_j})} \sim t_{N-k-1}$$
We can use the general t statistic to test against one-sided or two-sided alternatives.
p-Values for t Tests
- Given the observed value of the t statistic, what is the smallest significance level at which the null hypothesis would be rejected?
- We call this “smallest signiicance level” p-value.
- p-value represents the probability of observing a value as extreme as $t_{\hat{\beta}_j}$ under the $H_0$
- $$
\begin{array}{ll}
H_0: & \beta_j=0 . \\
H_1: & \beta_j \neq 0 .
\end{array}
$$- The p-value in this case is$$P(|T|>|t|),$$
- where we let $T$ denote a $\mathrm{t}$ distributed random variable with $N-k-1$ degrees of freedom and let $t$ denote the numerical value of the test statistic.
- The p-value nicely summarizes the strength or weakness of the empirical evidence against the null hypothesis.
- The p-value is the probability of observing a $t$ statistic as extreme as we did if the null hypothesis is true.
- Signiicance level and critical value一一对应
Economic versus Statistical Signiicance
- The statistical significance of a variable $x_j$ is determined entirely by the size of $t_{\hat{\beta}_j}$, whereas the economic significance or practical significance of a variable is related to the size (and sign) of $\hat{\beta}_j$.
- We often care about both statistical significance and economic significance.
Confidence interval
- We can construct a confidence level depending on $\alpha$. We call it a $(1-\alpha)$ confidence interval:$$[\hat{\beta}_j-c \cdot \operatorname{se}(\hat{\beta}_j), \hat{\beta}_j+c \cdot \operatorname{se}(\hat{\beta}_j)]$$
- The critical value $c$ is the $(1-\alpha / 2)$ percentile in a $\mathrm{t}$ distribution with $d f=N-k-1$.
- The meaning of a 95% conidence interval: if we sample repeatedly many times, then the true $β_j$ will appear in 95% of the confidence intervals.
- 对于很多次取样来说的可能性,但对于某一次特定的取样不能确定是否一定在置信区间里面。
三种方法一样:
- Fix a significance level $\alpha$, calculate the critical value $c$, and then reject $H_0$ if $|t_{\hat{\beta}_j}|>c$.
- Fix a significance level $\alpha$, calculate the $\mathrm{p}$-value, reject $H_0$ if $p<\alpha$.
- reject if 0 is not in the confidence level.
Testing Multiple Linear Restrictions: The F Test
- $$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\beta_3 x_3+u$$We want to test$$H_0: \quad \beta_1=0 \text { and } \beta_2=0$$$$H_1: H_0\text{ is not true.}$$
- Method:
- Consider the restricted model when $H_0$ is true$$y=\gamma_0+\gamma_3 x_3+u$$
- If $H_0$ is true, the two models are the same. That means when we include $x_1$ and $x_2$ into the model, the sum of squared residuals should not change much.
- However, if $H_0$ is false that means that at least one of $\beta_1, \beta_2$ is nonzero and the sum of squared residuals should fall when we include these new variables
- 看SSR是否相等
- F-test
- $$F \equiv \frac{(S S R_r-S S R_{u r}) / q}{S S R_{u r} /(N-k-1)}= \frac{(R_{u r}^2-R_r^2) / q}{(1-R_{u r}^2) /(N-k-1)}$$
- $q$ is the number of linear restrictions, which is the difference in degrees of freedom in the restricted model versus the unrestricted model.
- $S S R_r$ is the sum of squared residuals from the restricted model and $S S R_{u r}$ is the sum of squared residuals from the unrestricted model.
- Since $S S R_r$ can be no smaller than $S S R_{u r}$, the $\mathrm{F}$ statistic is always nonnegative.
- We can show that the sampling distribution of the F-stat: $F \sim F_{q, N-k-1}$. We call this an $\mathrm{F}$ distribution with $q$ degrees of freedom in the numerator and $N-k-1$ degrees of freedom in the denominator.
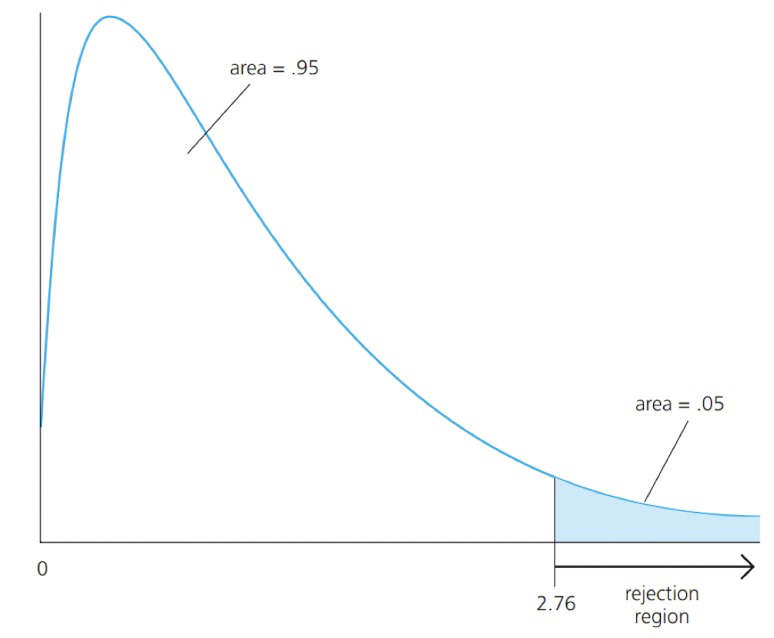
- t分布的平方就是F分布,因此单变量也可以用F分布。
- In the $\mathrm{F}$ testing context, the $\mathrm{p}$-value is defined as$$P(\mathcal{F}>F) $$where $\mathcal{F}$ denote an $\mathrm{F}$ random variable with $(q, N-k-1)$ degrees of freedom, and $\mathrm{F}$ is the actual value of the test statistic.
- p-value is the probability of observing a value of $\mathrm{F}$ at least as large as we did, given that the null hypothesis is true.
- $\rightarrow$ Reject $H_0$ if $p<\alpha$
- 通常情况下使用SSR形式的F检验比较好,因为有时候restricted的形式与unrestricted不同,不能直接用R2来计算。
Testing Multiple Linear Restrictions: The LM statistic
- Lagrange multiplier (LM) statistic
- The LM statistic can be used in testing multiple exclusion restrictions (as in an $F$ test) under large sample.
- 对于模型$$y=\beta_0+\beta_1 x_1+\ldots+\beta_k x_k+u$$We want to test whether the last $q$ of these variables all have zero population parameters:$$H_0: \beta_{k-q+1}=\beta_{k-q+2}=\ldots=\beta_k=0$$
- $L M$ statistic
- First estimate the restricted model:$$y=\tilde{\beta_0}+\tilde{\beta_1} x_1+\cdots+\tilde{\beta_{k-q}} x_{k-q}+\tilde{u}$$If the coefficients of the excluded independent variables $x_{k-q+1}$ to $x_k$ are truly zero in the population model, then they should be uncorrelated to $\tilde{u}$.
- So regress $\tilde{u}$ on all $x$$$\tilde{u} \sim x_1, x_2, \ldots, x_k$$Let $R_u^2$ denote the R-squared of this regression. The smaller the $R_u^2$, the more likely $H_0$ is true. So a large $R_u^2$ provides evidence against $H_0$.
- $L M=N \cdot R_u^2$. We can show that $L M$ follows chi-square distribution with $q$ degrees of freedom: $\mathcal{X}_q^2$.
- Reject $H_0$ if $L M>$ critical value $(p<$ significance level)

- 在大样本时,LM和F检验结果很相似
Ch5 Multiple Regression Analysis: OLS Asymptotics
Asymptotic Properties
- Finite sample properties: properties hold for any sample of data.
- Examples
- Unbiasedness of OLS
- OLS is BLUE
- Sampling distribution of the OLS estimators
- Asymptotic properties or large sample properties: not defined for a particular sample size; rather, they are defined as the sample size grows without bound.
- 渐近性质
Consistency
- 一致性
- Let $W_N$ be an estimator of $\theta$ based on a sample $Y_1, Y_2, \ldots, Y_N$ of size $N$. Then, $W_N$ is a consistent estimator of $\theta$ if for every $\epsilon>0$$$P(|W_N-\theta|>\epsilon) \rightarrow 0 \text { as } N \rightarrow \infty .$$
- We also say consistency means:$$\operatorname{plim}(W_N)=\theta$$
- Intuitively, consistency means when the sample size becomes larger, the estimator gets closer and closer to the true value.
- 一致性和无偏性没有必然联系
Consistency of OLS
- Under Assumptions MLR.1 through MLR.4, the OLS estimator $\hat{\beta}_j$ is consistent for $\beta_j$, for all $j=0,1, \ldots, k$.
- When the sample size is larger, the OLS estimator is centered around the true parameter closer and closer.
Central Limit Theorem
- Use the notation$$\hat{\theta}_N \stackrel{a}{\sim} N(0, \sigma^2)$$to mean that as the sample size $N$ gets larger, $\hat{\theta}_N$ is approximately normally distributed with mean 0 and variance $\sigma^2$.
- Central Limit Theorem
- Let ${Y_1, Y_2, \ldots, Y_N}$ be a random sample with mean $\mu$ and variance $\sigma^2$. Then,$$Z_N=\frac{\bar{Y}_N-\mu}{\sigma / \sqrt{N}} \stackrel{a}{\sim} N(0,1)$$
- Intuitively, it means when the sample size gets larger, the distribution of the sample average is closer to a normal distribution.
- 不管Y的分布如何,当样本量足够大,都会趋向于正态分布
Asymptotic Normality of OLS
- Under the Gauss-Markov Assumptions MLR.1 through MLR. 5 , for each $j=0,1, \ldots, k$
- $$\begin{aligned}
& \frac{\hat{\beta}_j-\beta_j}{s d(\hat{\beta}_j)} \stackrel{a}{\sim} \operatorname{Normal}(0,1) . \\
& \frac{\hat{\beta}_j-\beta_j}{\operatorname{se}(\hat{\beta}_j)} \stackrel{a}{\sim} \operatorname{Normal}(0,1) .
\end{aligned}$$ - OLS estimators are approximately normally distributed in large enough sample sizes.
- 这个定理说明当样本量足够大的时候,不需要u的正态分布假定。
Summary
- Under MLR.1-MLR.4, OLS estimators are consistent.
- Under MLR.1-MLR.5, OLS estimators have an asymptotic normal distribution.
Ch6 Multiple Regression Analysis: Further Issues
Efects of Data Scaling on OLS Statistics
changing unit of measurement
- Consider the simple regression model:$$y=\beta_0+\beta_1 x+u$$
- Now suppose $y^*=w_1 y$ and $x^*=w_2 x$, Then for this model:$$y^*=\beta_0^*+\beta_1^* x^*+u$$
- $\hat{\beta}_0^*$ and $\hat{\beta}_0$, and $\hat{\beta}_1^*$ and $\hat{\beta}_1$ 的关系是?
- $$\hat{\beta}_0^*=w_1 \hat{\beta}_0, \quad \hat{\beta}_1^*=\frac{w_1}{w_2} \hat{\beta}_1$$
- $$\operatorname{se}(\hat{\beta}_0^*) =w_1 \operatorname{se}(\hat{\beta}_0), \quad\operatorname{se}(\hat{\beta}_1^*) =\frac{w_1}{w_2}\operatorname{se}(\hat{\beta}_1)$$
- $$t_\hat{\beta_0}^*=t_\hat{\beta_0} \quad t_\hat{\beta_1}^* =t_\hat{\beta_1}$$
- $$R^{2*}=R^2$$
- the statistical signiicance does not change.
Unit Change in Logarithmic Form
- 只影响截距,不影响系数
Beta Coefficients
- Sometimes, it’s useful to obtain regression results when all variables are standardized: subtracting off its mean and dividing by its standard deviation.
- $$
\begin{aligned}
y_i & =\hat{\beta_0}+\hat{\beta_1} x_{i 1}+\cdots+\hat{\beta_k} x_{i k}+\hat{u_i} . \\
(y_i-\bar{y}) / \hat{\sigma_y} & =(\hat{\sigma_1} / \hat{\sigma_y}) \hat{\beta_1}[(x_{i 1}-\bar{x_1}) / \hat{\sigma_1}]+\cdots \\
& +(\hat{\sigma_k} / \hat{\sigma_y}) \hat{\beta_k}[(x_{i k}-\bar{x_k}) / \hat{\sigma_k}]+(\hat{u_i} / \hat{\sigma_y}) \\
z_y & =\hat{b_1} z_1+\cdots+\hat{b_k} z_k+\text { error }
\end{aligned}
$$ - where $z_y$ denotes the z-score of $y$. The new coefficients are$$\hat{b}_j=(\hat{\sigma}_j / \hat{\sigma}_y) \hat{\beta}_j$$
- If $x_1$ increases by one standard deviation, then $\hat{y}$ changes by $\hat{b}_1$ standard deviation.
- 归一化了
More on Functional Form
- 对于log形式 $$z=log(y)=\beta_0+\beta_1 x+u$$
- 当x变化$\Delta$ 时,$$\%\Delta E(y|x)=100[exp(\beta_1\Delta)-1]$$
- 当 $\Delta$ 趋近0时,$$\%\Delta E(y|x)\approx 100\beta_1\Delta$$
- 对于x取值小于0的,可以使用 inverse hyperbolic sine: $$IRS(x)=arcsinh(x)=log(x+\sqrt{x^2+1})$$
- 当x对y的影响是非线性的,可以考虑二次方。
More on Goodness of Fit
- 在Ch4中通过F检验来判断是否可以restrict模型,那么对于non-nested model怎么办呢?
- 例如: $$\begin{aligned}
& y=\beta_0+\beta_1 x_1+\beta_2 x_2+u \\
& y=\gamma_0+\gamma_1 x_4+e
\end{aligned}$$ - 这时候需要用 Adjusted R-square
- 选择 $\bar{R}^2$ 最高的
Prediction Analysis
confidence interval for E(y|x)
- Suppose we have estimated the equation$$\hat{y}=\hat{\beta}_0+\hat{\beta}_1 x_1+\hat{\beta}_2 x_2+\ldots+\hat{\beta}_k x_k$$Let $c_1, c_2, \ldots, c_k$ denote particular values for each of the $k$ independent variables.
- The parameter we would like to estimate is$(\theta)=E(y \mid x_1=c_1, \ldots, x_k=c_k)=\beta_0+\beta_1 c_1+\beta_2 c_2+\ldots+\beta_k c_k$
- The estimator of $\theta$ is$$\hat{\theta}=\hat{\beta}_0+\hat{\beta}_1 c_1+\hat{\beta}_2 c_2+\ldots+\hat{\beta}_k c_k$$
- $$y=\theta+\beta_1(x_1-c_1)+\beta_2(x_2-c_2)+\ldots+\beta_k(x_k-c_k)+u$$
- So we can regress $y_i$ on $(x_{i 1}-c_1), \ldots,(x_{i k}-c_k)$. The standard error and confidence interval of the intercept of this new regression is what we need.
Prediction Interval
- $$y=E(y \mid x_1, \ldots, x_k)+u$$
- The previous method form a confidence interval for $E(y \mid x_1, \ldots, x_k)$.
- Sometimes we are interested in forming the confidence interval for an unknown outcome on $y$.
- We need to account for the variation in $u$.
- Let $x_1^0, \ldots, x_k^0$ be the new vales of the independent variables, which we assume we observe. Let $u^0$ be the unobserved error.
$$
y^0=\beta_0+\beta_1 x_1^0+\ldots+\beta_k x_k^0+u^0 .
$$ - Our best prediction of $y^0$ is estimated from the OLS regression line
$$
\hat{y}^0=\hat{\beta}_0+\hat{\beta}_1 x_1^0+\ldots+\hat{\beta}_k x_k^0
$$ - The prediction error in using $\hat{y}^0$ to predict $y^0$ is
- Note $E(\hat{y}^0)=y^0$, because the $\hat{\beta}_j$ are unbiased. Because $u^0$ has zero mean, $E\left(\hat{e}^0\right)=0$.
- Note that $u^0$ is uncorrelated with each $\hat{\beta}_j$, because $u^0$ is uncorrelated with the errors in the sample used to obtain the $\hat{\beta}_j$.
- Therefore, the variance of the prediction error (conditional on all in-sample values of the independent variables) is:
$$
\operatorname{Var}(\hat{e}^0)=\operatorname{Var}(\hat{y}^0)+\operatorname{Var}(u^0)=\operatorname{Var}(\hat{y}^0)+\sigma^2 .
$$
- The standard error of $\hat{e}^0$ is:$$se(\hat{e}^0)={[se(\hat{y}^0)]^2+\hat{\sigma}^2}^{1 / 2}$$
- The prediction interval for $y^0$ is
$$
\sqrt{\hat{y}^0 \pm c \cdot s e\left(\hat{e}^0\right)}
$$
Ch7 Multiple Regression Analysis with Qualitative Information
A Single Dummy Independent Variable
We often capture binary information by defining binary variable or a zero-one variable.$$\text { female }= \begin{cases}0, & \text { if the individual is man } \\ 1, & \text { if the individual is woman }\end{cases}$$
zero-one leads to natural interpretations of the regression parameters
假设 $$\text { wage }=\beta_0+\delta_0 \text { female }+u$$
If we estimate the model using OLS$$\begin{aligned}
& \hat{\beta_0}=\overline{w a g e_{m e n}} \\
& \hat{\delta_0}=\overline{w a g e_{women}}-\overline{w a g e_{m e n}}\end{aligned}$$If we regress $y$ on a dummy variable $x$, then the OLS estimate of the intercept represents the sample average of $y$ when $x=0$, the OLS estimate of the slope coefficient represents the difference between the sample average of $y$ when $x=1$ and $x=0$.
当增加变量时,例如 $$w a g e=\beta_0+\delta_0 \text { female }+\beta_1 e d u c+u$$
$δ_0$ is the difference in hourly wage between women and men, given the same amount of education.
线性相关
- $wage=\beta_0 + \beta_1female+u$ 是可以的
- 选定了 male 作为 baseline group
- $wage=\beta_0 male + \beta_1female+u$ 是可以的
- $wage=\beta_0+\beta_1 male + \beta_2female+u$ 是不行的
Without intercept
- $wage=\beta_0 male + \beta_1female+u$ 没有截距,在解释和计算检验的时候不方便,并且 $R^2$ 可能是负的。
- In general, if there is no intercept in the regression model, the $R^2$ could be negative.
- To address the issue, some researchers use the uncentered R-squared when there is no intercept in the model$$R_0^2=1-\frac{S S R}{S S T_0},$$where $S S T_0=\sum_{i=1}^N y_i^2$.
Using Dummy Variables for Multiple Categories
多个组别的时候,两种选择
第一种,k-1个独立的变量:
- $$\text { wage }=\beta_0+\beta_1 \text { marrmale }+\beta_2 \text { marrfemale }+\beta_3 \text { singfem }+u \text {. }$$
第二种,乘积项:
- $$\text { wage }=\beta_0+\beta_1 \text { female }+\beta_2 \text { married }+\beta_3 \text { female } \cdot \text { married }+u$$
注意如果一个变量只能在几个离散值之间选择,最好把每个值的情况独立成一个哑元,否则相当于暗示了斜率变化是线性的。
- 例如CR可以取0,1,2,3,4
- $$MBR=\beta_0+\beta_1 C R+\text { other factors }+u \text {. }$$
- $$MBR=\beta_0+\delta_1 C R 1+\delta_2 C R 2+\delta_3 C R 3+\delta_4 C R 4+\text{other factors}+u$$
- 第二种模型更好。
Interactions Involving Dummy Variables
- 在 $wage=\beta_0+\beta_1female+\beta_2educ+u$ 中我们假定了 educ 对于男女的影响是相同的。
- 为了区别,需要添加一个乘积项:$$E(\text { wage } \mid \text { female }, \text { educ })=\beta_0+\delta_0 \text { female }+\beta_1 \text { educ }+\delta_1 \text { female } \cdot \text { educ. }$$
Testing for Differences in Regression Functions across Groups
- $$\text { wage }=\beta_0+\beta_1 \text { educ }+\beta_2 \text { exper }+\beta_3 \text { tenure }+u$$
- We want to test whether all the coefficients are the same for men and women.
- We can include interactive terms for all variables:$$
\begin{aligned}
\text { wage }= & \beta_0+\delta_0 \text { female }+\beta_1 \text { educ }+\delta_1 \text { educ } \cdot \text { female }+ \\
& \beta_2 \text { exper }+\delta_2 \text { exper } \cdot \text { female }+ \\
& \beta_3 \text { tenure }+\delta_3 \text { tenure } \cdot \text { female }+u .
\end{aligned}$$
- The null hypothesis:$$H_0: \delta_0=0, \delta_1=0, \delta_2=0, \delta_3=0$$We can use F test to test the hypothesis: estiamte the unrestricted and restricted model, and then calculate the F-stat.
Chow statistic
- 对于只有一个二元变量和很多其他连续变量的回归,我们想判断其他所有的变量是否关于两组完全相同
- We can show that the sum of squared residuals from the unrestricted model can be obtained from two separate regressions, one for each group: $S S R_{u r}=S S R_1+S S R_2$
- The F-statstic:$$F=\frac{S S R_p-(S S R_1+S S R_2)}{S S R_1+S S R_2} \cdot \frac{N-2(k+1)}{k+1}$$$S S R_p$ : SSR from pooling the groups and estimating a single equation.
- This is also called a Chow statistic.
- Note: use the Chow test if
- the model satisfies homoskedasticity
- we want to test no differences at all between the groups
Program Evaluation
- 在社会学实验中控制变量法
Ch8 Heteroskedasticity
Consequence of Heteroskedasticity for OLS
- Heteroskedasticity does not cause bias or inconsistency in the OLS estimators
- 对于一致性和无偏性无影响
- The interpretation of our goodness-of-fit measures is also unaffected by the presence of heteroskedasticity.
- 对于goodness of fit 无影响
- $R^2$ and adj- $R^2$ are different ways of estimating the population R-squared, $1-\sigma_u^2 / \sigma_y^2$.
- both variances in the population $R^2$ are unconditional variances
- SSR/ $N$ consistently estimates $\sigma_u^2$, and $S S T / N$ consistently estimates $\sigma_y^2$, whether or $\operatorname{not} \operatorname{Var}(u \mid x)$ is constant
- With heteroskedasticity, $\operatorname{Var}\left(\hat{\beta}_j\right)$ is biased.
- 对于方差有影响
- 标准差,t数据,置信区间都不再可靠
- 大样本也不能解决
- OLS is no longer BLUE.
Heteroskedasticity-Robust Inference after OLS Estimation
- Consider the simple linear regression model:$$y_i=\beta_0+\beta_1 x_i+u_i$$Assume SLR.1-SLR.4 are satisfied, and there exists heteroskedasticity:$$\operatorname{Var}(u \mid x_i)=\sigma_i^2$$$\operatorname{Var}(u)$ takes on different values when $x$ varies
- We don’t know the exact functional form of $\sigma_i^2$, it can be any function of $x$
Estimating $\operatorname{Var}\left(\hat{\beta}_j\right)$ under Heteroskedasticity
- One valid estimator (White,1980):$$\widehat{\operatorname{Var}}(\hat{\beta_1})=\frac{\sum_{i=1}^N(x_i-\bar{x})^2 \hat{u_i}^2}{[\sum_{i=1}^N(x_i-\bar{x})^2]^2} \equiv \frac{\sum_{i=1}^N(x_i-\bar{x})^2 \hat{u_i}^2}{SST_x^2}$$where $$SST_x=\sum_{i=1}^N(x_i-\bar{x})^2$$.
- For multiple regression model:$$\begin{gathered}y_i=\beta_0+\beta_1 x_{i 1}+\beta_2 x_{i 2}+\ldots+\beta_k x_{i k}+u_i . \\ \operatorname{Var}(\hat{\beta_j})=\frac{\sum_{i=1}^N \hat{r_{ij}}^2 \sigma_i^2}{[\sum_{i=1}^N \hat{r_{ij}}^2]^2} \equiv \frac{\sum_{i=1}^N \hat{r_{ij}}^2 \sigma_i^2}{SSR_j^2}\end{gathered}$$The estimator:$$\widehat{\operatorname{Var}}(\hat{\beta_j})=\frac{\sum_{i=1}^N \hat{r_{ij}}^2 \hat{u_i}^2}{[\sum_{i=1}^N \hat{r_{ij}}^2]^2}=\frac{\sum_{i=1}^N \hat{r_{ij}}^2 \hat{u_i}^2}{SSR_j^2}$$
- $\hat{r_{ij}}$ is the residual from regressing $x_j$ on all other independent variables
- $S S R_j$ is the sum of residual squared of this regression
- The square root of $\widehat{\operatorname{Var}}\left(\hat{\beta}_j\right)$ is called the heteroskedasticity-robust standard error, or simply, robust standard errors.
- Robust-standard error 是一致的
Compare the variance formula
- Under homoskedasticity, $\operatorname{Var}(\hat{\beta_1})$ is simplified as$$\operatorname{Var}(\hat{\beta_j})=\frac{\sum_{i=1}^N \hat{r_{ij}}^2 \sigma_i^2}{SSR_j^2}=\frac{\sigma^2}{SSR_j}$$
- Under heteroskedasticity,$$\operatorname{Var}(\hat{\beta_j})=\frac{\sum_{i=1}^N r_{i j}^2 \sigma_i^2}{SSR_j^2}=\frac{1}{SSR_j} \sum_{i=1}^N \frac{\hat{r_{ij}}^2}{SSR_j} \sigma_i^2=\frac{1}{SSR_j} \sum_{i=1}^N w_{ij} \sigma_i^2$$where $w_{ij}=\frac{\hat{\tau_{ij}}^2}{S S R_j}$. We know that $w_{ij}>0$ and $\sum_{i=1}^N w_{ij}=1$.
- 即,进行了加权平均。
- Robust standard errors can be either larger or smaller than the usual standard errors.
More on RSE
- 在有些情况下,特别是异方差性不强的情况下,robust-standard-error的表现不如传统的standard-error
- 小样本时rse存在误差
- rse的样本方差更大
- 在实践中通常在大样本时报告rse,在小样本时都报告。
Weighted Least Squares Estimation
Generalized Least Squares (GLS)
- Assume MLR.1-MLR.4 are satisfied:$$y_i=\beta_0+\beta_1 x_{i 1}+\ldots+\beta_k x_{i k}+u_i$$
- Assume that the variance of $u$ takes the following form:$$\operatorname{Var}(u \mid x_1, \ldots, x_k)=\sigma^2 h(x_1, \ldots, x_k)$$
- We write $\sigma_i^2=\sigma^2 h\left(x_{i 1}, \ldots, x_{i k}\right)=\sigma^2 h_i$.
- Consider an alternative regression model:$$\frac{y_i}{\sqrt{h_i}}=\beta_0 \frac{1}{\sqrt{h_i}}+\beta_1 \frac{x_{i 1}}{\sqrt{h_i}}+\ldots+\beta_k \frac{x_{i k}}{\sqrt{h_i}}+\frac{u_i}{\sqrt{h_i}}$$
- Let $\mathbf{x}$ denote all the explanatory variables. Conditional on $\mathbf{x}, E\left(u_i / \sqrt{h_i} \mid \mathbf{x}\right)=E\left(u_i \mid \mathbf{x}\right) / \sqrt{h_i}=0$.
- $\operatorname{Var}\left(u_i / \sqrt{h_i} \mid \mathbf{x}\right)=\sigma^2$, satisfying homoskedasticity.
- Denote the OLS estimator after the transformation as ${\beta_j^*}$
- We can prove that ${\beta_j^*}$ minimizes$$\sum_{i=1}^N(y_i-b_0-b_1 x_{i 1}-\cdots-b_k x_{i k})^2 / h_i$$
- Weighted least squares estimator(WLS):
- the weight for each $\hat{u}_i$ is $1 / h_i$. We give less weight for observations with higher variance. Intuitively, they provide less information.
- ${\beta_j^*}$ is still one estimator for the original model, and have the same interpretation
- Because ${\beta_j^*}$ satisfies MLR.1-MLR.5, so it is BLUE under heteroskedasticity with the form $\sigma_i^2=\sigma^2 h_i$
- ${\beta_j^*}$ is also called generalized least squares estimators (GLS)
Feasible Generalized Least Squares (FGLS)
- 实际中需要估计 $h_i$
- Assume $h_i$ takes the following form:$$\begin{aligned}\operatorname{Var}(u \mid x) & =\sigma^2 \exp \left(\delta_0+\delta_1 x_1+\ldots+\delta x_k\right) \\ u^2 & =\sigma^2 \exp \left(\delta_0+\delta_1 x_1+\ldots+\delta x_k\right) v,\end{aligned}$$where $v$ has a mean of one.
- We take $\exp (\cdot)$ to guarantee that $\operatorname{Var}(u)>0$
- Equivalently,
$$
\log \left(u^2\right)=\alpha+\delta_1 x_1+\ldots+\delta x_k+e .
$$
- As usual, we replace the unobserved $u$ with the OLS residuals $\hat{u}$, and estimate $\log \left(\hat{u}^2\right) \sim 1, x_1, \ldots x_k$, calculate the fitted value $\hat{g}_i$. Then $\hat{h}_i=\exp \left(\hat{g}_i\right)$.
Procedure
- Run the regression of $y$ on $1, x_1, \ldots, x_k$, get the residual $\hat{u}_i$
- Calculate $\log \left(\hat{u}_i^2\right)$
- Estimate $\log \left(\hat{u}_i^2\right) \sim 1, x_1, \ldots x_k$, get the fitted value $\hat{g}_i$
- Compute $\hat{h}_i=\exp \left(\hat{g}_i\right)$
- Use $1 / \hat{h}_i$ as weights, estimate $y \sim 1, x_1, \ldots, x_k$ using WLS.
FGLS is consistent, and has smaller asymptotic variance than OLS.
WLS or RSE
- There is no guarantee that WLS is more efficient than OLS.
- It is alwasy advised to report robust standard errors with WLS.
- two solutions for heteroskedasticity:
- Use OLS to estiamte the model, calculate the robust standard errors (or use the max of the conventional s.e. and robust s.e.)
- Use FGLS to estimate the model, report conventional s.e. or robust s.e.
- In practice, the first method is preferred in most cases
Testing for Heteroskedasticity
Breusch-Pagan Test for Heteroskedasticity
- We want to know in model $y=\beta_0+\beta_1 x_1+. .+\beta_k x_k+u$, whether $u^2$ is correlated with $x$
- Estimate $y=\beta_0+\beta_1 x_1+. .+\beta_k x_k+u$, get the residual $\hat{u}$
- Estimate the following model and get $R_{\hat{u}^2}^2$ :$$\hat{u}_i^2=\delta_0+\delta_1 x_1+\ldots+\delta_k x_k+v$$
- We test $H_0: \delta_1=\ldots=\delta_k=0$
- Calculate the $L M$ statistic: $N \cdot R_{\hat{u}^2}^2$; or calculate the $F$ $\operatorname{statistic}\left[R_{\hat{u}^2}^2 / k\right] /\left[\left(1-R_{\hat{u}^2}^2\right) /(N-k-1)\right]$.
- Reject homoskedasticity if
- test statistic $>$ critical value
- $p<$ significance level
The White Test for Heteroskedasticity
- OLS standard errors are asymptotically valid if MLR.1-MLR.5 holds.
- It turns out that the homoskedasticity assumption can be replaced with the weaker assumption that the squared error, $u^2$, is uncorrelated with all the independent variables $\left(x_j\right)$, the squares of the independent variables $\left(x_j^2\right)$, and all the cross products $\left(x_j x_h, \forall j \neq h\right)$.
- When the model contain $k=2$ independent variables, the White test is based on an estimation of$$\hat{u}^2=\delta_0+\delta_1 x_1+\delta_2 x_2+\delta_3 x_1^2+\delta_4 x_2^2+\delta_5 x_1 x_2+v$$The White test for heteroskedasticity is the LM statistic for testing that all of the $\delta_j$ are zero, except for the intercept.
- Problem: with many independent variables, we uses many degrees of freedom. Solution: use $\hat{y}^2$ :$$\hat{u}^2=\delta_0+\delta_1 \hat{y}+\delta_2 \hat{y}^2+v$$We then use the $\mathrm{F}$ or LM statistic for the null hypothesis $H_0: \delta_0=\delta_2=0$.
Ch12 Serial Correlation
Serial Correlation
Times series data
- Time series data: observations on variables over time.
- random sampling is often violated
Classical Assumptions about Time Series Data
- The stochastic process ${(x_{t 1}, \ldots, x_{t k}, y_t): t=1,2, \ldots, T}$ follows the linear model:$$y_t=\beta_0+\beta_1 x_{t 1}+\ldots+\beta_k x_{t k}+u_t$$
- No perfect collinearity.
- Zero conditional mean.$$E(u_t \mid \mathbf{X})=0, t=1,2, \ldots, T$$
- where $\mathbf{X}$ is the explanatory variables for all time periods.
- $E\left(u_t \mid \mathbf{X}\right)=0$ means both $E\left(u_t \mid x_t\right)=0$ and also $E\left(u_t \mid x_s\right)=0, \forall t \neq s$.
- Unbiasedness of $\mathrm{OLS}$
- Under assumptions TS.1, TS.2 and TS.3, the OLS estimators are unbiased and consistent.
Serial Correlation
- No serial correlation assumption:$$\operatorname{Cov}((x_t-\bar{x}) u_t,(x_s-\bar{x}) u_s \mid X)=0, \forall t \neq s$$Or$$E(u_s u_t \mid X)=0, \forall t \neq s$$
- For time-series data, this is often not true.
Auto-regression,AR
- Think about a simple regression model:$$y_t=\beta_0+\beta_1 x_t+u_t$$
- Assume that$$u_t=\rho u_{t-1}+e_t, t=1,2, \ldots, T$$where $|\rho|<1$, and $e_t$ are i.i.d with $E\left(e_t\right)=0$. This is called an autoregressive process of order one $(\operatorname{AR}(1))$.
Properties of AR
- Because $e_t$ is i.i.d, $u_t$ will be correlated with current and past $e_t$, but not future values. If the time series has been going on forever$$u_t =\rho u_{t-1}+e_t=\rho^k u_{t-k}+\rho^{k-1} e_{t-(k-1)}+\ldots+e_t =\sum_{j=0}^{\infty} \rho^j e_{t-j}$$
- $$E(u_t) =E(\sum_{j=0}^{\infty} \rho^j e_{t-j})=\sum_{j=0}^{\infty} \rho^j E(e_{t-j})=0$$
- We can show that$$\begin{aligned}
\operatorname{Var}(u_t) & =\operatorname{Var}(\sum_{j=0}^{\infty} \rho^j e_{t-j})=\sum_{j=0}^{\infty} \rho^{2 j} \operatorname{Var}(e_{t-j}) \\
& =\operatorname{Var}(e_t) \sum_{j=0}^{\infty} \rho^{2 j}=\frac{\operatorname{Var}(e_t)}{1-\rho^2}\end{aligned}$$ - Also$$\begin{aligned}\operatorname{Cov}(u_t, u_{t+1}) & =\operatorname{Cov}(u_t, \rho u_t+e_t)=\rho \operatorname{Var}(u_t) \\
\operatorname{Cov}(u_t, u_{t+j}) & =\rho^j \operatorname{Var}(u_t)
\end{aligned}$$ - Assume further that $\bar{x}=0$ and homoskedasticity, that is $\operatorname{Var}\left(u_t \mid X\right)=\operatorname{Var}\left(u_t\right)=\sigma^2$. Then
- $$
\begin{aligned}
\operatorname{Var}(\hat{\beta} \mid \mathbf{X}) & =\frac{\operatorname{Var}(\sum_{t=1}^T x_t u_t \mid \mathbf{X})}{S S T_x^2} \\
& =\frac{\sum_{t=1}^T x_t^2 \operatorname{Var}(u_t)+2 \sum_{t=1}^{T-1} \sum_{j=1}^{T-t} x_t x_{t+j} E(u_t u_{t+j})}{S S T_x^2} \\
& =\frac{\sigma^2}{S S T_x}+\frac{2 \sigma^2}{S S T_x^2} \sum_{t=1}^{T-1} \sum_{j=1}^{T-t} \rho^j x_t x_{t+j}
\end{aligned}$$
Consequence of ignore serial correlation
- 仍然是无偏、一致的
- 但传统的方差有问题了
- 会低估方差
- 完善方法:
- 使用FGLS
- 使用OLS,修正se
FGLS
- Assume TS.1-TS.3. Further, assume $\operatorname{Var}\left(u_t \mid X\right)=\sigma^2$.$$
\begin{aligned}
& y_t=\beta_0+\beta_1 x_t+u_t . \\
& u_t=\rho u_{t-1}+e_t, t=1,2, \ldots, T .
\end{aligned}$$- where $e_t$ is i.i.d and $E\left(e_t\right)=0$.
- Transform the regression:$$\begin{aligned}
y_t-\rho y_{t-1} & =(1-\rho) \beta_0+\beta_1(x_t-\rho x_{t-1})+e_t, t \geq 2 . \\
\tilde{y}_t & =(1-\rho) \beta_0+\beta_1 \tilde{x}_t+e_t, t \geq 2\end{aligned}$$
We can use FGLS to estimate:
- Estimate the model using OLS and obtain the OLS residuals $\hat{u}_t$
- Use OLS to estimate $\hat{u_t} \sim \hat{u_{t-1}}$ and obtain $\hat{\rho}$.
- Calculate $\tilde{y_t}=y_t-\hat{\rho} y_{t-1}$ and $\tilde{x_t}=x_t-\hat{\rho} x_{t-1}$, then use OLS to regress $\tilde{y_t}$ on $\tilde{x_t}$.
Serial Correlation-Robust Inference after OLS
- 了解即可,记住HAC(heteroskedasticity and auto-correlation consistent)
- We can show that$$AVar(\hat{\beta_1})=(\sum_{t=1}^T E(r_t^2))^{-2} Var(\sum_{t=1}^T r_t u_t)$$where $r_t$ is the error term in $x_{t 1}=\delta_0+\delta_2 x_{t 2}+\ldots+\delta_k x_{t k}+r_t$. We want to find and estimator for $A \operatorname{Var}(\hat{\beta}_1)$.
- Let $\hat{r}_t$ denote the residuals from regressing $x_1$ on all other independent variables, and $\hat{u}_t$ as the OLS residual from regressing $y$ on all $x$.
- Define$$\hat{\nu}=\sum_{t=1}^T \hat{a_t}^2+2 \sum_{h=1}^g[1-h /(g+1)](\sum_{t=h+1}^T \hat{a_t} \hat{a_{t-h}}),$$where $\hat{a_t}=\hat{r_t} \hat{u_t}$.
- Then$$s e(\hat{\beta_1})=[se_c(\hat{\beta_1}) / \hat{\sigma}]^2 \sqrt{\hat{\nu}}$$where $se_c(\hat{\beta_1})$ is the conventional standard error of $\hat{\beta}_1$, and $\hat{\sigma}$ is the square root of the sum of the OLS residual squared.
- We use $g$ to capture how much serial correlation we are allowing in computing the standard error.
- For annual data, choose $g=1$ or $g=2$
- Use a larger $g$ for larger sample size.
- When $g=1$,$$\hat{\nu}=\sum_{t=1}^T \hat{a_t}^2+\sum_{t=2}^T(\hat{a_t} \hat{a_{t-1}})$$
- This formula is robust to arbitrary serial correlation and arbitrary heteroskedasticity. So people sometimes call this heteroskedasticity and auto-correlation consistent, or HAC, standard errors.
Spatial Correlation
Data with group structure
- group structure, 例如不同班级的学生,在同班之内是有相关性的
- Example: class size and test score$$y_{i g}=\beta_0+\beta_1 x_g+u_{i g}$$
- Use $i$ to denote student, who are randomly assign to different class $g . y_{i g}$ is the test score of student $i$ (who is in class $g$ ), $x_g$ is the class size (which has the same value for students in the same class.)
- Assume that $E(u \mid X)=0$
- However, observations within the same $g$ is not independent (students in the same class are exposed to the same teacher and classroom…)$$E(u_{i g} u_{j g})=\rho_u \sigma_u^2 \neq 0$$
- We call $\rho_u$ intraclass correlation coefficient.、
- 这种相关性就叫 spatial correlation
- 存在这种情况时,一致性和无偏性还是保证的,但方差和标准差有变化。
Fix spatial correlation
OLS and Cluster Standard Errors
- The general idea is to model correlation of error terms within a group, and assume no correlation across groups.
- group数量变多的时候是consistent的
- 当数量大于42的时候就可以认为group数量够多了
Use group mean
- Estimate$$\bar{y}_g=\beta_0+\beta_1 x_g+\bar{u}_g$$by WLS using the group size as weights.
- We can generalize the method to models with microcovariates$$y_{i g}=\beta_0+\beta_1 x_g+\beta_2 w_{i g}+u_{i g}$$
- Estimate$$y_{i g}=\mu_g+\beta_2 w_{i g}+\eta_{i g}$$The group effects, $\mu_g$, are coefficients on a full set of group dummies.
- Regress the estimated group effects on group-level variables$$\hat{\mu}_g=\beta_0+\beta_1 x_g+e_g$$In this step, we could either weight by the group size, or use no weights.
Ch9 Proxy Variable and Measurement Error
Endogeneity and Exogeneity
- Zero conditional mean condition:$$E(u \mid x)=0$$
- $x_j$ is endogenous if it is correlated with $u$.
- $x_j$ is exogenous if it is not correlated with $u$.
- Violating the zero conditional mean condition will cause the OLS estimator to be biased and inconsistent.
Proxy Variable
- 代理变量
Omitted Variable Bias
- $$\log (\text { wage })=\beta_0+\beta_1 e d u c+\beta_2 a b i l+u$$
- In this model, assume that $E(u \mid e d u c,abil)=0$
- 假设首要目的是估计 $\beta_1$ consistently,不关注 $\beta_2$.
- 但我们没有关于abil的数据, 所以只用 educ 回归 $\log ($ wage $)$
- There is an omitted variable bias if $\operatorname{cov}(abil,educ) \neq 0$ and $\beta_2 \neq 0$.
- One solution: use proxy variable for the omitted variable
- Proxy variable: related to the unobserved variable that we would like to control for in our analysis
- 只需要这个变量proxy variable与abil相关,即correlated,不需要完全相同
Proxy
Formally, we have a model$$y=\beta_0+\beta_1 x_1+\beta_2 x_2^*+u$$
Assume that $E\left(u \mid x_1, x_2^*\right)=0$
$x_1$ is observed and $x_2^*$ is unobserved
We have a proxy variable for $x_2^*$, which is $x_2$$$x_2^*=\delta_0+\delta_2 x_2+v_2$$
where $v_2$ is the error to allow the possibility that $x_2$ and $x_2^*$ is not exactly related. $E\left(v_2 \mid x_2\right)=0$.
Replace the omitted variable by the proxy variable:$$\color{red}{y=(\beta_0+\beta_2 \delta_0)+\beta_1 x_1+\beta_2 \delta_2 x_2+(u+\beta_2 v_2)}$$To get an unbiased and consistent estimator for $\beta_1$, we require$$E(u+\beta_2 v_2 \mid x_1, x_2)=0$$
Break this down into two assumptions:
- $E\left(u \mid x_1, x_2\right)=0$ : the proxy variable should be exogenous (intuitively, since $x_2^*$ is exogenous, the proxy variable is only good if it is also exogenous)
- 代理变量需要时外生的
- $E\left(v_2 \mid x_1, x_2\right)=0$ : this is equivalent as$$E(x_2^* \mid x_1, x_2)=E(x_2^* \mid x_2)=\delta_0+\delta_2 x_2$$Once $x_2$ is controlled for, the expected value of $x_2^*$ does not depend on $x_1$
- $E\left(u \mid x_1, x_2\right)=0$ : the proxy variable should be exogenous (intuitively, since $x_2^*$ is exogenous, the proxy variable is only good if it is also exogenous)
在上面的例子中,变成:$$\log (w a g e)=\alpha_0+\alpha_1 e d u c+\alpha_2 I Q+e$$
In the wage equation example, the two assumptions are:
- $E(u \mid e d u c, I Q)=0$
- $E($ abil|educ, $I Q)=E(a b i l \mid I Q)=\delta_0+\delta_3 I Q$
- The average level of ability only changes with IQ, not with education (once IQ is fixed).
在这样的变化中,$\beta_1$ 是无偏的
- 违反假设,会造成误差
Using Lagged Dependent Variables as Proxy Variables
- 滞后因变量
- $$\text { crime }=\beta_0+\beta_1 \text { unem }+\beta_2 \text { expend }+\beta_3 \text { crime }_{-1}+u$$
- By including crime $_{-1}$ in the equation, $\beta_2$ captures the effect of expenditure of law enforcement on crime, for cities with the same previous crime rate and current unemployment rate.
Measurement Error
Measurement Error in the Dependent Variable
- 因变量的测量误差
- Let $y^*$ denote the variable that we would like to explain.$$y^*=\beta_0+\beta_1 x_1+\ldots+\beta_k x_k+u,$$and we assume it satisfies the Gauss-Markov assumptions.
- Let $y$ to denote the observed measure of $y^*$
- Measurement error is defined as$$e_0=y-y^*$$
- Plug in and rearrange$$y=\beta_0+\beta_1 x_1+\ldots+\beta_k x_k+u+e_0$$
- 当e和自变量都无关的时候,结果仍然是一致且无偏的,但方差会变大
- 仍然适用OLS
Measurement Error in the Independent Variable
- 自变量的测量误差
- Consider a simple regression model:$$y=\beta_0+\beta_1 x_1^*+u$$We assume it satisfies the Gauss-Markov assumptions.
- We do not observe $x_1^*$. Instead, we have a measure of $x_1^*$; call it $x_1$
- The measurement error$$e_1=x_1-x_1^*$$Assume $E\left(e_1\right)=0$.
- Plug in $x_1^*=x_1-e_1$$$y=\beta_0+\beta_1 x_1+(u-\beta_1 e_1)$$
- To derive the properties of the OLS estimators, we need assumptions.
- First, assume that:$$E(u \mid x_1^*, x_1)=0$$This implies $E(y \mid x_1^*, x_1)=E(y \mid x_1^*): x_1$ does not affect $y$ after $x_1^*$ has been controlled for.
- Next, we consider two (mutually exclusive) cases about how the measurement error is correlated with $x$
- $\operatorname{Cov}(x_1, e_1)=0$
- $\operatorname{Cov}(x_1^*, e_1)=0$
Case 1:$\operatorname{Cov}(x_1, e_1)=0$
- Plug in $x_1^*=x_1-e_1$$$y=\beta_0+\beta_1 x_1+(u-\beta_1 e_1)$$
- Then $E\left(u-\beta_1 e_1 \mid x_1\right)=0$, so the OLS estimator of the slope coefficient of $x_1$ in the above model gives us unbiased and consistent estimator of $\beta_1$.
- If $u$ is uncorrelated with $e_1$, then $\operatorname{Var}\left(u-\beta_1 e_1\right)=\sigma_u^2+\beta_1^2 \sigma_{e_1}^2$.
- 一致性和无偏性仍然成立
Case 2:$\operatorname{Cov}(x_1^*, e_1)=0$
- The classical errors-in-variables (CEV) assumption is that $e_1$ is uncorrealted with the unobserved variables.
- Idea: the two components of $x_1$ is uncorrelated$$x_1=x_1^*+e_1$$
- Plug in $x_1^*=x_1-e_1$$$y=\beta_0+\beta_1 x_1+(u-\beta_1 e_1)$$
- Then$$\operatorname{Cov}(u-\beta_1 e_1, x_1)=-\beta_1 \operatorname{Cov}(x_1, e_1)=-\beta_1 \sigma_{e_1}^2 \neq 0$$
- 此时一致性和无偏性都破坏了
- The probability limit of $\hat{\beta}_1$
- $$\operatorname{plim}(\hat{\beta_1}) =\beta_1+\frac{\operatorname{Cov}(x_1, u-\beta_1 e_1)}{\operatorname{Var}(x_1)}=\beta_1-\frac{\beta_1 \sigma_{e_1}^2}{\sigma_{x_1}^{2 *}+\sigma_{e_1}^2}=\beta_1(\frac{\sigma_{x_1}^{2 *}}{\sigma_{x_1}^{2 *}+\sigma_{e_1}^2}) $$
- $\operatorname{plim}(\hat{\beta}_1)$ is closer to zero than $\beta_1$.
- This is called the attenuation bias in OLS due to CEV
- If the variance of $x_1^*$ is large relative to the variance in the measurement error, then the inconsistency in OLS will be small.
Case 3:$\operatorname{Cov}(x_1, e_1)=0 \text{ and } \operatorname{Cov}(x_1^*, e_1)=0$
- 这种情况下,OLS几乎一定会造成无偏性和一致性失效。
Ch15 Instrumental Variable
IV Estimator
Omitted Variable bias
- $$\log (\text { wage })=\beta_0+\beta_1 e d u c+\beta_2 a b i l+e$$
- In this model, assume that $E(e \mid e d u c, a b i l)=0$
- 只想一致地估计 $\beta_1$ 不在意 $\beta_2$.
- 假设没有abli的数据,只进行下面回归$$y=\beta_0+\beta e d u c+u$$where $u=\gamma a b i l+e$.
- Note that $E(u \mid e d u c)=E\left(\beta_2 a b i l+e \mid e d u c\right)=\beta_2 E(a b i l \mid e d u c)$. If $E(a b i l)$ changes when educ changes, then the zero conditional mean assumption is not satisfied.
- $$\begin{aligned}
\hat{\beta_{OLS}} & =\frac{\sum_{i=1}^N(y_i-\bar{y})(x_i-\bar{x})}{\sum_{i=1}^N(x_i-\bar{x})^2} =\beta+\frac{\sum_{i=1}^N(x_i-\bar{x}) u_i}{\sum_{i=1}^N(x_i-\bar{x})^2} \\
\hat{\beta_{OLS}} & \stackrel{plim}{\longrightarrow} \beta+\frac{\operatorname{cov}(x, u)}{\operatorname{var}(x)} .
\end{aligned}$$ - Since $E(u \mid x) \neq 0, E\left(\hat{\beta}_{O L S}\right) \neq \beta$, OLS is not unbiased
- Since $\operatorname{cov}(x, u) \neq 0$, OLS is not consistent.
- 此时无偏性和一致性都不满足
Instrumental Variable (IV)
- 用z来替换x
- $$y=\beta_0+\beta_1 x+u$$
- 仍然可以保证 $E(u)=0$,因为可以调整截距项
- With $E(u \mid x) \neq 0$, we no longer have $E(x u)=0$.
- Estimation idea: find another variable $z$, where$$\operatorname{Cov}(x, z) \neq 0 ; \quad \operatorname{Cov}(z, u)=0$$
- $\operatorname{Cov}(z, u)$ implies$\operatorname{Cov}(z, u)=E(u z)-E(z) E(u)=E(u z)=0$
Use $E(u z)=0$ and $E(u)=0$ to find the sample analogue, $$E(u z)=0 \quad \frac{1}{N} \sum_{i=1}^N z_i \hat{u_i}=0 $$$$E(u)=0 \quad \frac{1}{N} \sum_{i=1}^N \hat{u_i}=0$$and solve the equations.
$$\begin{aligned}
\hat{\beta_1}^{I V} & =\frac{\sum_{i=1}^N\left(y_i-\bar{y}\right)\left(z_i-\bar{z}\right)}{\sum_{i=1}^N\left(x_i-\bar{x}\right)\left(z_i-\bar{z}\right)} \\
\hat{\beta_0}^{I V} & =\bar{y}-\hat{\beta_1}^{I V} \bar{x}
\end{aligned}$$把这个叫做 IV estimator
OLS求的值是一种特殊的IV estimator,当z=x时。
Assumptions on IV
- Instrument relevance:
- 相关性
- $\operatorname{Cov}(x, z) \neq 0: z$ is relevant for explaining variation in $x$.
- $x=\pi_0+\pi_1 z+v$, 进行零检验 $H_0: \pi_1=0$.
- Instrument exogeneity:
- 外生性
- $\operatorname{Cov}(u, z)=0$ : 保证了一致性.
- 不能直接从数据中检验,需要根据金融理论。
Properties and Inference with the IV Estimator
- 一致性满足
- 无偏性不满足
- consider the expectation of $\hat{\beta_1}^{IV}$ conditional on $z$$$E(\hat{\beta_1}^{I V})=\beta+E(\frac{\sum_{i=1}^N(z_i-\bar{z}) u_i}{\sum_{i=1}^N(x_i-\bar{x})(z_i-\bar{z})})=\beta+E(E[\frac{\sum_{i=1}^n(z_i-\bar{z}) u_i}{\sum_{i=1}^N(x_i-\bar{x})(z_i-\bar{z})} \mid z])$$
- 由于x不是常数,因此不能进一步化简
- 方差:
- 增加假设$$E[u^2 \mid z]=\sigma^2$$
- 在如上假设情况下:$$AVar(\hat{\beta_1}^{IV})=\frac{\sigma^2}{N \sigma_x^2 \rho_{x, z}^2}$$
- 其中 $\sigma_x^2$ 是总体x的方差,$\sigma^2$ 是总体u的方差, $\rho_{x,z}^2$ 是总体x和z的相关性
- The asymptotic variance of $\hat{\beta}_1^{I V}$ is
- $$\widehat{AVar}(\hat{\beta_1}^{IV})=\frac{\hat{\sigma}^2}{SST_xR_{x,z}^2}$$
- where $S S T_x=\sum_{i=1}^n(x_i-\bar{x})^2$, and $R_{x, z}^2$ is the R-squared of $x_i$ on $z_i$.
- Note that the variance of the OLS estimator is
- $$\widehat{\operatorname{Var}}(\hat{\beta}_1^{O L S})=\frac{\hat{\sigma}^2}{S S T_x}$$
- So the IV estimator has a larger variance.
- If $x$ an $z$ are only slightly correlated, then $R_{x, z}^2$ can be small, and this translate into a large sampling variance of the IV estimator.
Two Stage Least Squares
Multiple Instrumental Variables
- 有可能不只一个IV
- 考虑模型$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+u$$
- Assume $x_1$ is endogenous and has two IVs: $z_1$ and $z_2$. Assume $x_2$ is exogenous.
- Two-stage least squares (2SLS): 使用两个IV的线性组合来构造新的IV
2SLS
接着上面的例子
The steps of 2SLS
- Stage 1: estimate (using OLS)$$x_1=\alpha_0+\alpha_1 z_1+\alpha_2 z_2+\alpha_3 x_2+v$$and calculate $\hat{x}_1$.
- 这个阶段的回归需要包含所有的外生变量
- Stage 2: use $\hat{x}_1$ as an IV for $x_1$. Or directly estimate$$y=\beta_0+\beta_1 \hat{x}_1+\beta_2 x_2+u$$
- Stage 1: estimate (using OLS)$$x_1=\alpha_0+\alpha_1 z_1+\alpha_2 z_2+\alpha_3 x_2+v$$and calculate $\hat{x}_1$.
多个内生变量时:
考虑有两个内生变量的模型:$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\beta_3 x_3+u$$where $x_1$ and $x_2$ are endogenous (whose IV are $z_1$ and $z_2$), $x_3$ is exogenous.
In the first stage, we need to include all instruments and exogenous variables on the right hand side
$$x_1=\alpha_0+\alpha_1 z_1+\alpha_2 z_2+\alpha_3 x_3+v$$$$x_2=\gamma_0+\gamma_1 z_1+\gamma_2 z_2+\gamma_3 x_3+v$$
IV的数量应该大于等于内生变量的数量
Issues with IV
Sample size
- 需要一个大样本,因为在2SLS的第一步中,$x=\alpha_0+\alpha_1z+e$
- 其中的$\alpha_0+α_1z$ 是与u无关的,e是与u相关的
- 在2SLS第二步中,我们希望用$\alpha_0+\alpha_1 z$ 来表示x,但实际上是用 $\hat{\alpha}_0+\hat{\alpha}_1 z$. 后项可能包含关于u的信息。
- 因此需要大样本。
Weak instruments
- Weak instruments: low correlation between $x$ and $z$
- Suppose there is some small correlated between $u$ and $z$$$\begin{aligned}\operatorname{plim}(\hat{\beta}_1^{I V}) & =\beta_1+\frac{\operatorname{Cov}(z, u)}{\operatorname{Cov}(z, x)} \\ & =\beta_1+\frac{\operatorname{Corr}(z, u)}{\operatorname{Corr}(z, x)} \cdot \frac{\sigma_u}{\sigma_x},\end{aligned}$$where $\sigma_u$ and $\sigma_x$ are the standard deviations of $u$ and $x$ in the population respectively.
- We can show that$$\operatorname{plim}(\hat{\beta}_1^{O L S})=\beta_1+\operatorname{Corr}(x, u) \cdot \frac{\sigma_u}{\sigma_x}$$
- If $\operatorname{Corr}(z, x)$ is small enough, then even if $\operatorname{Corr}(z, u)$ is small, the IV estimator could result in larger asymptotic bias than the OLS estimator.
- 对于无偏性在小样本下也有影响。
检验弱相关
- $$y=\beta_0+\beta_1 x_1+\beta_2 x_2+u$$
- Assume $x_1$ is endogenous with two instrumental variables $z_1$ and $z_2$, and $x_2$ is exogenous.
- Estimate$$x_1=\alpha_0+\alpha_1 z_1+\alpha_2 z_2+\alpha_3 x_2+e$$
- Test $H_0: \alpha_1=\alpha_2=0$
- 当F-stat大于10的时候可以说没有弱相关性
Testing for endogeneity
- 检验x与u是否相关
- Suppose $x_1$ is endogenous, and the IV is $z$$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+u$$
- First stage: $x_1=\alpha_0+\alpha_1 z+\alpha_2 x_2+v$. If $x_1$ is correlated with $u$, then it must be $v$ is correlated with $u$. Estimate the equation to get $\hat{v}$.
- Estimate $y=\delta_0+\delta_1 x_1+\delta_2 x_2+\delta_3 \hat{v}+e$. Test $H_0: \delta_3=0$.
Testing overidentifying restrictions
当z比x多的时候,可以比较好地推断 $Cov(z,u)=0$
Suppose $x_1$ is endogenous, and the IVs are $z_1$ and $z_2$.
Use either one of them, we calculate $\hat{\beta}_1^{I V 1}$ and $\hat{\beta}_1^{I V 2}$
If $\hat{\beta}_1^{I V 1}$ is very different from $\hat{\beta}_1^{I V 2}$, then at least one of them does not satisfy $\operatorname{Cov}(z, u)=0$.
If they are close to each other, then it could be both satisfies $\operatorname{Cov}(z, u)=0$, or neither.
当z很多的时候
- Testing overidentifying restrictions:
- 使用2SLS估计,并得到2SLS残项 $\hat{u}_1$.
- Regress $\hat{u}_1$ on all exogenous variables. Obtain the $R$-squared, say $R^2$.
- 若所有IV都与 $u_1$ 无关,则 $N \cdot R^2 \sim \chi_q^2$, where $q$ is the number of instrumental variables from outside the model minus the total number of endogenous explanatory variables.
- Reject $H_0$ if $N \cdot R^2$ exceeds the critical value.
- Testing overidentifying restrictions:
Ch17 Limited Dependent Variable Models
Linear Probability model
Limited Dependent Variable
- 因变量只能取特定值
- In the population, $y$ takes on two values: 0 and 1 . We are interested in how $x$ will affect $y$.
- Suppose $x$ and $y$ has this linear relation:$$y=\beta_0+\beta_1 x+u$$
- Suppose $E(u \mid x)=0$. Then$$E(y \mid x)=P(y=1 \mid x)=\beta_0+\beta_1 x$$$\beta_1$ represents when $x$ increases by one unit, the impact on the probability that $y=1$. In other words, $\beta_1.$ measures the marginal effect of $x$ on the probability that $y=1$
- y是否是二元变量都不影响对这个模型的解释
- Descriptive: $\beta_1$ is the expected difference in the probability that $y=1$ if $x$ changes by one unit.
- Causal: one unit increase in $x$ causes the probability of $y=1$ to change by $\beta_1$ on average.
- 这个模型违反了同方差性,因为方差是x的函数,可以用FGLS来估算。
Non-linear Model and Maximum Likelihood
- Consider the following non-linear model:$$E(y \mid x)=P(y=1 \mid x)=G(\beta_0+\beta_1 x)$$where $G$ is a function mapping values to the range of 0 and 1 , to make sure $E(y \mid x)$ belongs to 0 and 1 .
- $G$ can have different functional forms. We consider two common ones:
- logistic function (logit)
- $$G(z)=\frac{\exp (z)}{1+\exp (z)}$$
- standard normal CDF (probit)
- $$G(z)=\Phi(z)$$
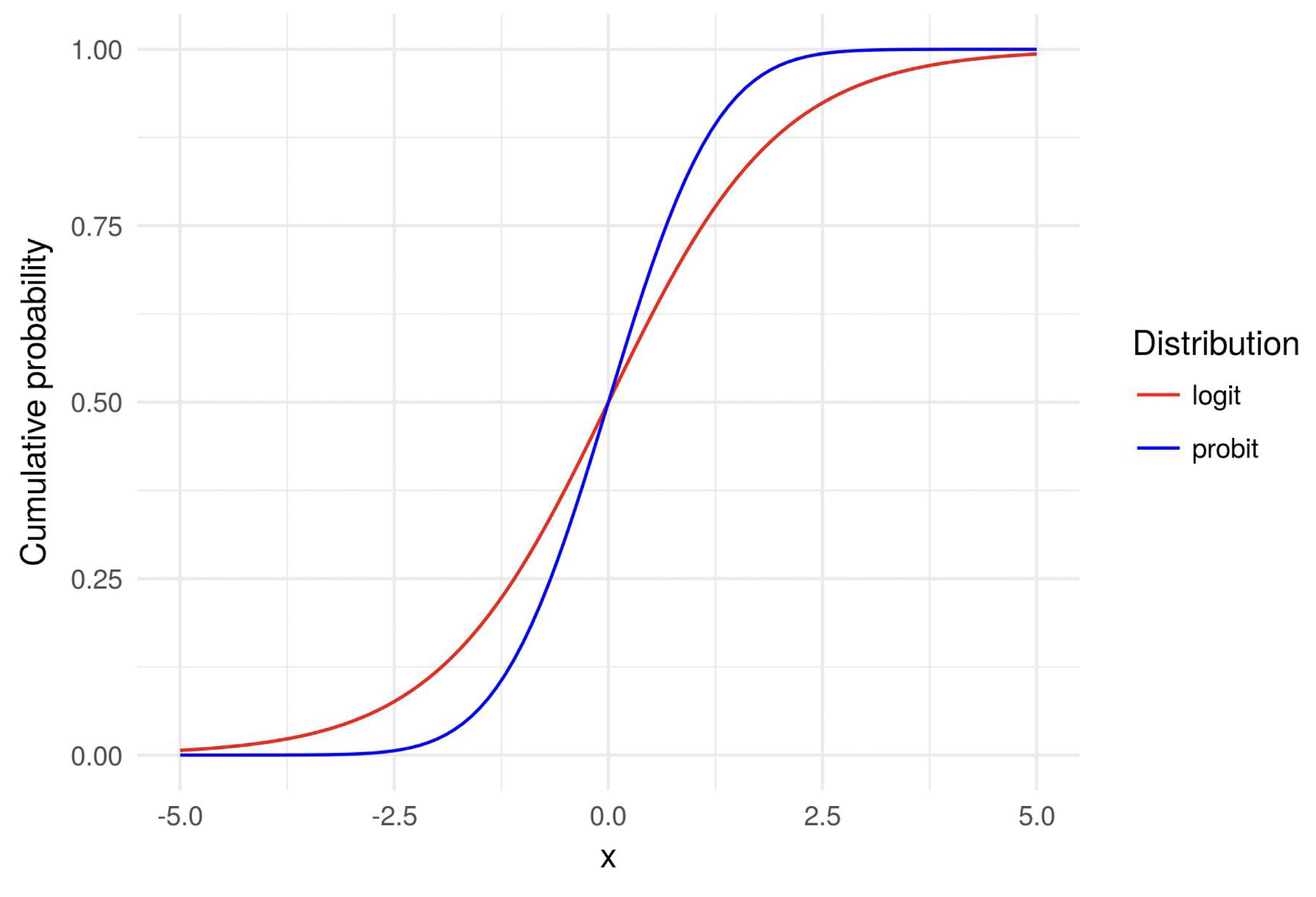
- logistic function (logit)
Properties of Logit and Probit
- y的这两种分布取决于残项e的分布
- Suppose random variable $e$ has a CDF:$$\operatorname{Pr}(e \leq z)=G(z)$$Here $G(z)$ can be either logit or probit.
- Let $y^*=\beta_0+\beta_1 x+e$, where $e$ is independent of $x$.
- $$\begin{aligned} P(y=1 \mid x) & =P(y^*>0 \mid x) =P(\beta_0+\beta_1 x+e>0 \mid x) \\ & =P(e>-\beta_0-\beta_1 x) =1-\operatorname{Pr}(e \leq-\beta_0-\beta_1 x) \\ & =1-G\left(-\beta_0-\beta_1 x\right)=G\left(\beta_0+\beta_1 x\right) .\end{aligned}$$
Partial effect of x on y
- the marginal effect of $x$ on the probability that $y=1$$$\frac{\partial p(x)}{\partial x_1}=g(\beta_0+\beta_1 x) \beta_1$$where $p(x)=P(y=1 \mid x), g(z) \equiv \frac{d G}{d z}(z)$.
- 即对上面的式子求导
- When we have more than one independent variables:$$\frac{\partial p(x)}{\partial x_j}=g(\beta_0+\boldsymbol{x} \boldsymbol{\beta}) \beta_j$$where $\boldsymbol{x} \boldsymbol{\beta}=\beta_1 x_1+\ldots+\beta_k x_k$.
- So the ratio of the partial effect of $x_j$ and $x_k$ is $\frac{\beta_j}{\beta_k}$.
- 这种方法和OLS比的弱点在于这个偏导数的前项g取决于x
- 解决办法:
- 找特殊点,例如均值点。
- Partial effect at the average:$$g(\hat{\beta_0}+\overline{\boldsymbol{x}}\hat{\beta_{\mathbf{1}}})=g(\hat{\beta_0}+\hat{\beta_1} \bar{x_1}+\hat{\beta_2} \bar{x_2}+\cdot+\hat{\beta_k} \bar{x_k})$$
- 求偏导的均值
- Average marginal effect:$$[N^{-1} \sum_{i=1}^N g(\hat{\beta_0}+x_{i} \hat{\beta_1})] \hat{\beta_j}$$
- 找特殊点,例如均值点。
Maximum Likelihood Estimation
估计:在样本中观察到某些值时y=1,另外一些值时y=0
使用最大似然估计找到 $\beta$ 使得这种成立的概率最大。
下面就是一个普通的求最大似然估计的过程,当作概统复习:
Suppose we have a random sample of size $N$. Fix every $x$ and $\beta$, the probability that $y=1$ is:$$E(y \mid x)=P(y=1 \mid x)=G(\beta_0+\beta_1 x) \equiv G(\beta x) $$
Then for any observation $y=0$ or $y=1$, its probability density function is:$$f(y \mid \beta x)=G(\beta x)^y[1-G(\beta x)]^{(1-y)}$$
For a random sample, all observations are independent of each other. Then the probability that we observe the sample is: ( $i$ is the index for each observation)$$f({y_1, \ldots, y_N} \mid \beta x_i)=\prod_{i=1}^N[G(\beta x_i)]^{y_i}[1-G(\beta x_i)]^{(1-y_i)}$$
- Maximum likelihood estimation (MLE): maximize the probability that we observe the data:$$\max_{\boldsymbol{\beta}} f({y_1, \ldots, y_N} \mid \beta x_i)=\max_{\boldsymbol{\beta}} \prod_{i=1}^N[G(\beta x_i)]^{y_i}[1-G(\beta \boldsymbol{x}_{\boldsymbol{i}})]^{(1-y_i)}$$
- Take the natural logarithm and define:$$\ell_i(\beta)=\log ([G(\beta x_i)]^{y_i}[1-G(\beta x_i)]^{(1-y_i)})=y_i \log [G( x_i)]+(1-y_i) \log [1-G(\beta x_i)]$$
- Then we can equivalently write:$$\max_\beta \sum_{i=1}^N \ell_i(\beta)=\max_{\boldsymbol{\beta}} \sum_{y_i=1} \log [G(\beta x_{\boldsymbol{i}})]+\sum_{y_i=0} \log [1-G(\beta x_{\boldsymbol{i}})]$$
- MLE is consistent and asymptotically efficient.
MLE and OLS
- OLS用来估算线性模型
- MLE用来估计线性和非线性模型
- 当u服从正态分布时,MLE与OLS结果相同
Appendix
$\color{red}{\text{Law of Iterated Expectation:}}$
- $$\color{red}{E(y)=E[E(y|x)]}$$
Summation operation
- $$\sum_{i=1}^N(x_i-\bar{x})(y_i-\bar{y})=\sum_{i=1}^N(x_i-\bar{x})y_i=\sum_{i=1}^N(x_iy_i-\bar{x}\bar{y})$$
Variance
- $$\begin{aligned}
\operatorname{Var}(X+a) & =\operatorname{Var}(X) \\
\operatorname{Var}(a X) & =a^2 \operatorname{Var}(X) \\
\operatorname{Var}(X) & =\operatorname{Cov}(X, X) \\
\operatorname{Var}(a X+b Y) & =a^2 \operatorname{Var}(X)+b^2 \operatorname{Var}(Y)+2 a b \operatorname{Cov}(X, Y) \\
\operatorname{Var}\left(\sum_{i=1}^N a_i X_i\right) & =\sum_{i, j=1}^N a_i a_j \operatorname{Cov}(X_i, X_j) \\
& =\sum_{i=1}^N a_i^2 \operatorname{Var}(X_i)+\sum_{i \neq j} a_i a_j \operatorname{Cov}(X_i, X_j) \\
& =\sum_{i=1}^N a_i^2 \operatorname{Var}(X_i)+2 \sum_{i=1}^N \sum_{j=i+1}^N a_i a_j \operatorname{Cov}(X_i, X_j) .
\end{aligned}$$
- $$\begin{aligned}



