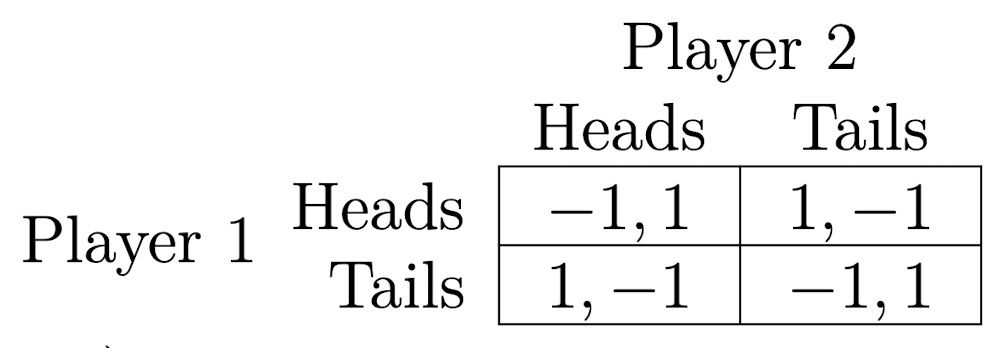
L2: Static Games of Complete Information
Normal-form games
- Static: one shot, simultaneous move
- complete information: each player’s payoff function is common knowledge among all players.
Normal-form representation
the players (参与者) in the game;
the strategies (策略) available to each player;
the payoff(收益/效用) received by each player for each combination of strategies that could be chosen by the players.
$\color{red}{\textbf{complete: 是不是common knowledge}}$
$\color{red}{\textbf{perfect: 每次decision对方是否知道}}$
Normal-form Defination
The normal-form (标准式) (also called strategic-form) representation of an n-player game speciies the players’ strategy sets/spaces $S_1$ , . . . , $S_n$ and their $\color{red}{\text{payoff functions}}$ u1, . . . , un. We denote this game by
- $$G=<S_1,S_2,…S_n,u_1,…u_n>$$
- Can also represent by bi-matrix form.
Concept of strategy
Some notations:
- $$s=(s_1,s_2,…,s_{i-1},s_i,s_{i+1},…,s_n)$$
- $$s_{-i}=(s_1,s_2,…,s_{i-1},s_{i+1},…,s_n)$$
- $$S=S_1\times S_2 \times …\times S_{i-1}\times S_{i}\times S_{i+1}\times…\times S_n$$
- $$S_{-i}=S_1\times S_2 \times …\times S_{i-1}\times S_{i+1}\times…\times S_n$$
- $$\color{red}{s=(s_i,s_{-i})}$$
策略
- Best response:
- 在其他人选定的情况下对我最有利的情况
- $$\max_{s_i\in S_i} u_i(s_i,s_{-i})$$
- denoted by $$R_i(s_{-i})$$
- Strictly dominated stratey
- 在所有情况下都不如另一个策略,另一个策略不一定是NE
- A rational player will never choose a strictly dominated strategy.
- Strictly dominant strategy
- 在所有情况下都严格比其他所有策略好
- If a strictly dominant strategy exists, then it must be unique.
- A rational player will always choose a strictly dominant strategy, if any.
- Weakly dominant strategy
- 在所有情况下都大于等于其他所有策略
关系
- A strictly dominated strategy can never be a best response
- A strictly dominant strategy is always a best response
IESDS and Nash Equilibrium
IESDS
不断消去strictly dominated strategy
main drawbacks
- A key assumption: rationality of all players is common knowledge.
- The prediction of IESDS may not be very precise, and sometimes it predicts nothing about the games.
NE
- Defination
- $$(s_1^*,…,s_n^*)\text{ is a NE if }s_i^*\in R_i(s_{-i}),i=1,2,…,n$$
- Equivalently, $$u_i(s_i^*,s_{-i}^*)=\max_{s_i\in S_i}u_i(s_i,s_{-i}^*)$$
- Each player’s strategy must be a best response, given other players’ equilibrium strategies.
- No single player wants to deviate unilaterally
- strategically stable or self-enforcing.
Issues on NE
- A Nash equilibrium needs not to be Pareto optimal (帕累托最优)
- More generally, Nash equilibrium does not rule out the possibility that a subset of players can deviate jointly in a way that makes every player in the subset better off.
- The Nash equilibrium implicitly assumes that players know that each player is to play the equilibrium strategy. Given this knowledge, no player wants to deviate.
Relationship between IESDS and NE
- NE can survive IESDS
- $${\text{Nash Equilibria}\subset\text{subset of IESDS}}$$
- Nash equilibrium is a stronger solution concept than IESDS.
- Nash equilibrium does not require that rationality is common knowledge.
- 在有限的情况,IESDS如果消到只剩下一个,那一定是NE
Applications
Cournot Duopoly
- 题目
- Suppose two firms (1 and 2) produce a homogeneous good, and compete in quantities.
- Let $q_i$ be the quantity produced by firm i, where i = 1 , 2.
- The aggregate quantity of the good is denoted by $Q = q_1 + q_2$. The inverse demand (反需求函数) of the good is $P(Q)=a-Q$
- The cost function of firm i is $C_i(q_i) = cq_i$
- 将题目化成 normal-form game
- 找best response 的交点
- 结论:
- $$(q_1^*,q_2^*)=(\frac{1}{3}(a-c),\frac{1}{3}(a-c))$$
Bertrand Model of Duopoly
- 计算过程类似 cournot
Mixed strategies
Definition
- In a normal-form game $G=\left\langle S_1, \ldots, S_n ; u_1, \ldots, u_n\right\rangle$, suppose $S_i={s_{i1}, …, s_{iK_i}}$
- Each strategy $s_{i k} \in S_i$ is a pure strategy (纯策略) for player
- A mixed strategy (混合策略) for player $i$ is a probability distribution $p_i=\left(p_{i 1}, \ldots, p_{i K_i}\right)$, for $k=1, \ldots, K_i$, where $p_{i 1}+\cdots+p_{i K_i}=1$ and $p_{i k} \geq 0$.
- Note that there are only $K_i$ pure strategies for player $i$, but infinitely many mixed strategies.
Expected payoff
- If player 1 thinks that player 2 will play a mixed strategy $p_2=\left(p_{21}, \ldots, p_{2 K}\right)$, then player 1’s expected payoff (期望效用) of playing a pure strategy $s_{1 j}$ is
- $$v_1\left(s_{1 j}, p_2\right)=\sum_{k=1}^K p_{2 k} u_1\left(s_{1 j}, s_{2 k}\right) .$$
- Player 1’s expected payoff (期望效用) of playing a mixed strategy $p_1=\left(p_{11}, \ldots, p_{1 J}\right)$ is
- $$\begin{aligned}
v_1\left(p_1, p_2\right) & =\sum_{j=1}^J p_{1 j} \sum_{k=1}^K p_{2 k} u_1\left(s_{1 j}, s_{2 k}\right) \
& =\sum_{j=1}^J \sum_{k=1}^K p_{1 j} p_{2 k} u_1\left(s_{1 j}, s_{2 k}\right)
\end{aligned}$$
- A mixed strategy $p_1 = (p_{11} , . . . , p_{1j})$ is a best response (最优应对) to $p_2$ if
- $$v_1(p_1,p_2)\geq v_1(p_1^\prime,p_2)$$
Mixed strategy NE
Definition
In a normal-form game $G=\left\langle S_1, \ldots, S_n ; u_1, \ldots, u_n\right\rangle$, the mixed strategy profile $\left(p_1^*, \ldots, p_n^*\right)$ is a mixed-strategy Nash equilibrium if each player’s mixed strategy is a best response to the other players’ mixed strategies in terms of expected payoff, i.e.,
$$v_(p_i^*, p_{-i}^*)\geq v_i(p_i, p_{-i}^*)$$
for every $p_i$ over $S_i$, and for all $i=1, \ldots, n$.
求解:
- mixed strategy 必须每个分量都是indifferent,每个选项的预期收益是相同的
Applications
proposition
- The pure strategies played with a positive probability in a mixed strategy Nash equilibrium survive IESDS.
- A pure strategy is a strictly dominated strategy (dominated by a mixed strategy) if and only if it is never a best response (to mixed strategies).
- 考虑有mixed strategy情况下
- 充要条件
- 即如果有某些action的组合比该action的收益严格高,那么该action就不可能是best response。
存在性定理
- 定理:
- In the n-player normal-form game $G = ⟨S_1 , . . . , S_n; u_1, . . . , u_n⟩$, if n is finite and $S_i$ is finite for every i, then there exists at least one Nash equilibrium, possibly involving mixed strategies.
- The conditions are suicient but not necessary conditions for the existence of a Nash equilibrium.
- 充分不必要条件
- Recall that in both Cournot and Betrand competition models, Nash equilibrium exists but the strategy space is infinite.
L3: Dynamic Games of Complete Information
Intro
dynamic games: sequential choice or repeated play
Complete Information: each player’s payoff function is common knowledge among all players
center issue is credibility.
Use extensive-form (扩展式) representation for dynamic games.
Draw game trees.
Games of Perfect Information
Player 2 choose after he knows what player 1 choose.
If its imperfect Information, we draw a dotted line between 2 and 2 in the tree above.
Note that
- $A_2$ may depend on the action a1, i.e., $A_2(a_1)$.
- Some action $a_1$ may even end the game, so that $A_2(a_1)$ is an empty set (i.e., no choice of player 2).
- The action $a_1$ is perfectly observed by player 2.
In the game of the farmer and the snake: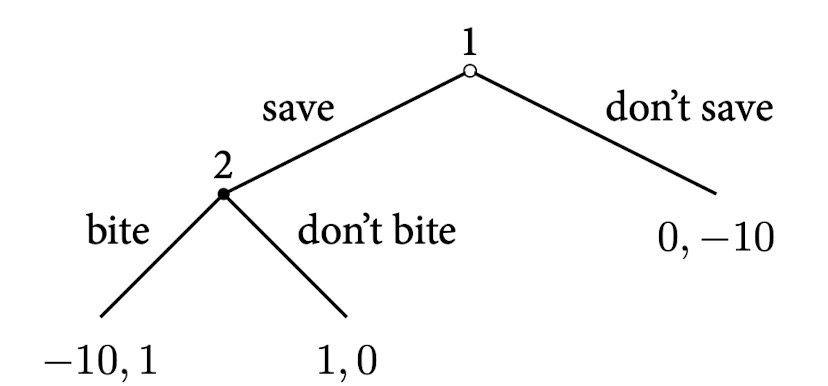
Some key features
- the moves occur in sequence;
- all previous moves are observed before the next move ischosen
- the players’ payoffs from each combination of moves are common knowledge.
Backwards Induction
- In the second stage, player 2 observes what player 1 choose and choose action to solving $$\max \limits_{a_2\in A_2}\quad u_2(a_1, a_2)$$
- Assume this optimization problem has a unique solution, denoted by $R_2(a_1)$.
- This is player 2’s best response to player 1’s action $a_1$
- In the first stage, knowing player 2’s best response, player 1’s problem become$$\max \limits_{a_1\in A_1}\quad u_1(a_1, R_2(a_1))$$
- Assume it also has a unique solution, denoted by $a_1^*$.
- We call $(a_1, R_2(a_1^*))$ the backwards-induction outcome (逆向归纳的结果) of the game
- In the backwards-induction outcome, $a_1^*$ is determined by maximizing $u_1 (a_1 , R_2(a_1))$, and $a_2^* = R_2(a_1^*)$.
- However, $a_1^*$ may not maximize $u_1(a_1, a_2^*)$.
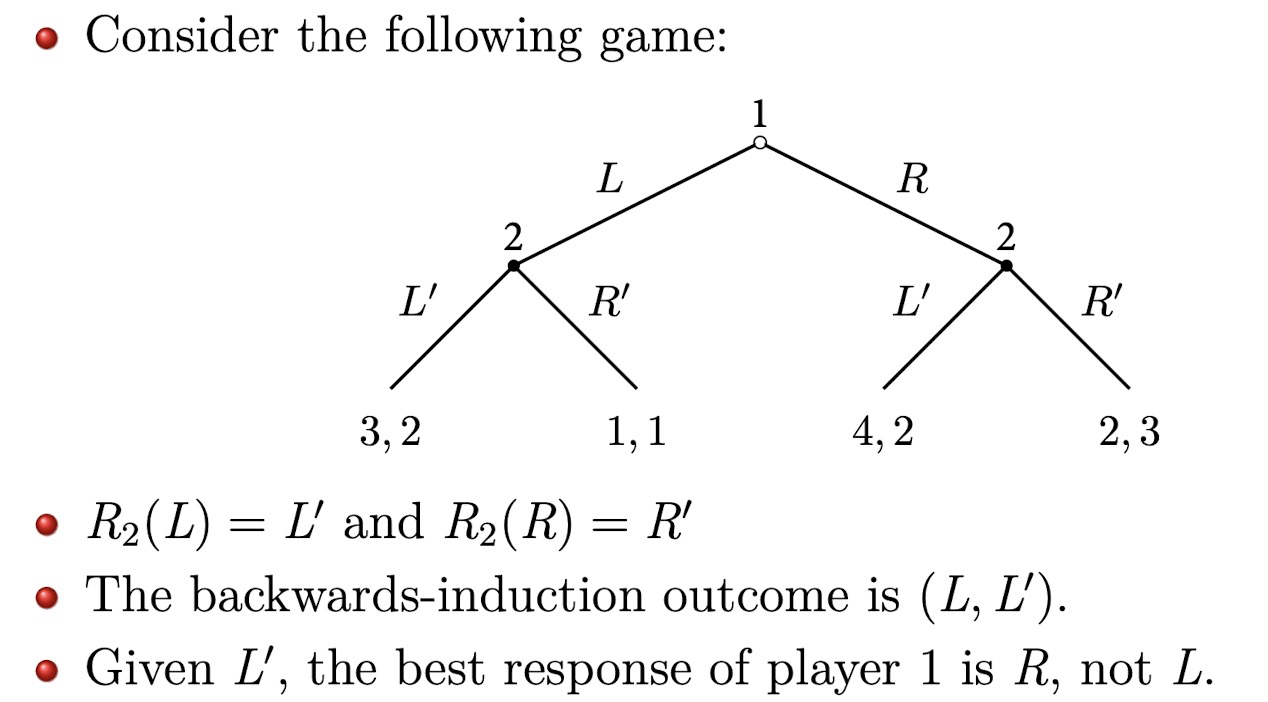
Stackelberg Model of Duopoly
Consider a dominant firm moving first and a follower moving second.
- The game is as follows:
- Firm 1 choose quantity $q_1 \ge 0$
- Firm 2 observes $q_1$ and then chooses a quantity $q_2 \ge 0$.
- The payoff of firm i is the profit $$\pi_i\left(q_1, q_2\right)=q_i[P(Q)-c]$$
- where $Q=q_1+q_2$ and
$$
P(Q)= \begin{cases}a-Q, & \text { if } Q<a \\ 0, & \text { if } Q \geq a\end{cases}
$$
- Firm 1 choose quantity $q_1 \ge 0$
Now solve this game.
- First, find the best response function $R_2 (q_1)$ for firm 2, i.e.for any given $q_1$, find $q_2$ that solves $$\max _{q_2 \geq 0} \pi_2\left(q_1, q_2\right)$$where
$$\pi_2\left(q_1, q_2\right)= \begin{cases}q_2\left(a-q_1-q_2-c\right), & \text { if } q_1+q_2<a ; \\ -c q_2, & \text { if } q_1+q_2 \geq a .\end{cases}$$ - Then we have
$$
R_2\left(q_1\right)= \begin{cases}\frac{a-c-q_1}{2}, & \text { if } q_1<a-c \\ 0, & \text { if } q_1 \geq a-c .\end{cases}
$$ - $R_2(q_1)$ is the same as that in the Cournot model.
- Second, firm 1 knows $R_2 (q_1)$ and solves$$\max \limits_{q_1 \ge 0} \quad \pi_1(q_1, R_2(q_1))$$ where$$\pi_1\left(q_1, R_2\left(q_1\right)\right)= \begin{cases}q_1\left[a-q_1-\frac{a-q_1-c}{2}-c\right], & \text { if } q_1<a-c \\ q_1\left[a-q_1-c\right], & \text { if } a-c \leq q_1<a \\ -c q_1, & \text { if } q_1 \geq a\end{cases}$$
- Clearly, for $q_1>a-c$, firm 1’s profit is always negative.
- Thus we only need to solve
$$
\max _{a-c \geq q_1 \geq 0} q_1\left[a-q_1-\frac{a-q_1-c}{2}-c\right],
$$
which leads to the following first-order condition
$$
a-c-2 q_1=0 .
$$ - The optimal choice of firm 1 is
$$
q_1^*=\frac{a-c}{2}
$$ - The quantity chosen by firm 2 is
$$
q_2^*=R_2\left(q_1^*\right)=\frac{a-c}{4} .
$$ - The market price is
$$
P^*=a-q_1^*-q_2^*=c+\frac{a-c}{4} .
$$ - Firms’ profits and the total profit are
$$
\pi_1^*=\frac{(a-c)^2}{8}, \pi_2^*=\frac{(a-c)^2}{16}, \text { and } \Pi^*=\frac{3(a-c)^2}{16}
$$
Compare with Cournot Model
$$
\begin{aligned}
&\begin{array}{ccc}
\text {Variable} & \text{Cournot Model} & \text{Stackelberg Model}\\
\hline q_1^* & \frac{a-c}{3} & \frac{a-c}{2} \\
q_2^* & \frac{a-c}{3} & \frac{a-c}{4} \\
\pi_1^* & \frac{(a-c)^2}{9} & \frac{(a-c)^2}{8} \\
\pi_2^* & \frac{(a-c)^2}{9} & \frac{(a-c)^2}{16} \\
\Pi^* & \frac{2(a-c)^2}{9} & \frac{3(a-c)^2}{16} \\
P^* & c+\frac{a-c}{3} & c+\frac{a-c}{4} \\
\hline
\end{array}
\end{aligned}
$$
- Note: First-move advantage:
- 先手有优势,比起同时的情况。
Games of Imperfect Information
- Consider the following game
- Players 1 and 2 simultaneously choose actions $a_1$ and $a_2$ from the feasible sets $A_1$ and $A_2$, respectively.
- Players 3 and 4 observe the outcome of the first stage $(a_1 , a_2)$ and then simultaneously choose actions $a_3$ and $a_4$ from the feasible sets $A_3$ and $A_4$, respectively.
- Payoffs are $u_i(a_1, a_2, a_3, a_4)$ for i = 1, 2, 3, 4.
- There are simultaneous moves within each stage.
Solve
- Still, backwards induction.
- For each given $\left(a_1, a_2\right)$, players 3 and 4 try to find the Nash equilibrium in stage 2.
- Assume the second-stage game has a unique Nash equilibrium$(a_3^*(a_1, a_2), a_4^*(a_1, a_2))$$
- Then, player 1 and player 2 play a simultaneous-move game with payoffs$$
u_i(a_1, a_2, a_3^*(a_1, a_2), a_4^*(a_1, a_2)), \text { for } i=1,2$$ - Suppose $(a_1^*, a_2^*)$ is the unique Nash equilibrium of this simultaneous-move game.
- Then$$(a_1^*, a_2^*, a_3^*(a_1^*, a_2^*), a_4^*(a_1^*, a_2^*))$$is the subgame-perfect outcome (子博恋精炼结果) of the two-stage game.
Example: Bank Run
- payoff in date 1:
Withdraw Don’t Withdraw 4,4 5,3 Don’t 3,5 next stage - payoff in date 2
Withdraw Don’t Withdraw 8,8 11,5 Don’t 5,11 8,8
Solve: backwards
- date2, both obtain 8 in nash equilibrium.
- Thus, in date1, they play the following game:
Withdraw Don’t Withdraw 4,4 5,3 Don’t 3,5 8,8
There are two NE.
Extensive-form Representation
Defination
The extensive-form (扩展式) representation of a game specifies:
- the players in the game;
- when each player has the move; *
- what each player can do at each of his or her opportunities to move; *
- what each player knows at each of his or her opportunities to move; *
- the payoffs received by each player for each combination of moves that could be chosen by the players
the three * part describes strategies of each player in detail.
use trees for extensive-form representations.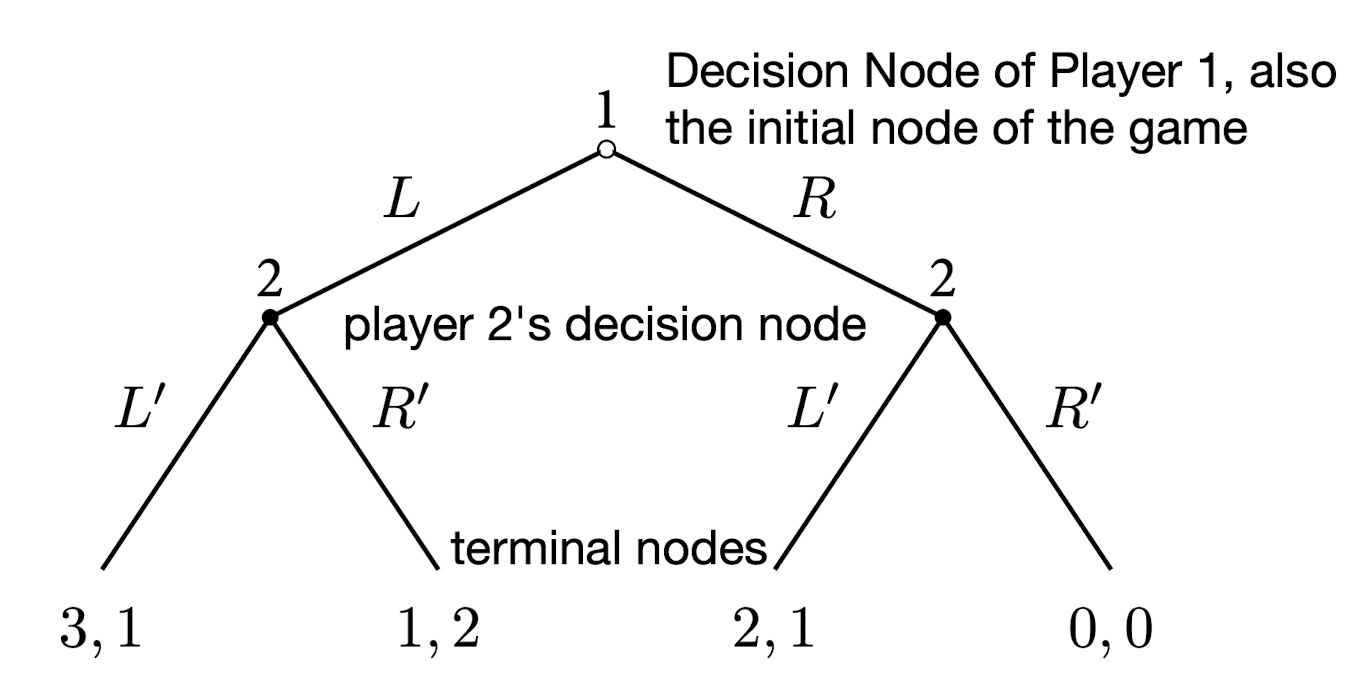
Information Set
- Complete and perfect information
- A dynamic game of complete and perfect information is a game in which the players move in sequence, all previous moves are observed before the next move is chosen, and payoffs are common knowledge.
- Such games can be easily represented by a game tree.
- Imperfect information
- some previous moves are not observed by the player with the current move.
- To present this kind of ignorance of previous moves and to describe what each player knows at each of his/her move, we introduce the notion of a player’s information set (信息集)
Definition of Information Set
An information set (信息集) for a player is a collection of decision nodes satisfying:
- The player needs to move at every node in the information set.
- When the play of the game reaches a node in the information set, the player with the move does not know which node in the set has (or has not) been reached.
- implies that the player must have the same set of feasible actions at each decision node in an information set; Otherwise the player could infer from the set of actions available that some nodes had or had not been reached.
- Any two nodes from different information sets of a player can be distinguished from each other.
Application of Information Set
- A game is:
- of perfect information (完美信息) if every information set is a singleton;
- of imperfect information (不完美信息) if there is at least one non-singleton information set.
- meaning there is at least a dotted line in the tree form.
Prisoners Dilemma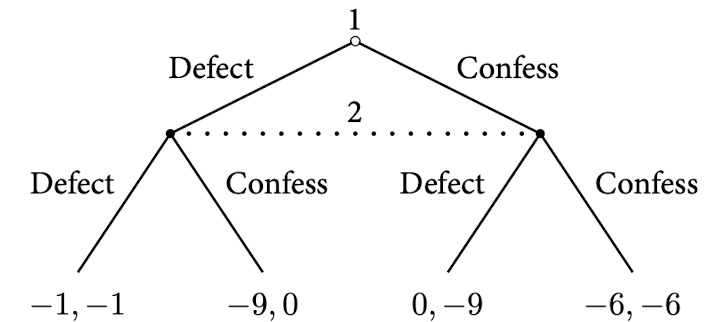
Strategy
Definition
A strategy (策略) for a player is a complete plan of actions. It specifies a feasible action for the player in every contingency in which the player might be called on to act.
- For dynamic games with complete information:
- A player’s strategy is a function which assigns an action to each information set (not each decision node) belonging to the player.
- 对每个选择节点,指定一个策略
- An action and a strategy do not make a big diference in static games, while they do in dynamic games.
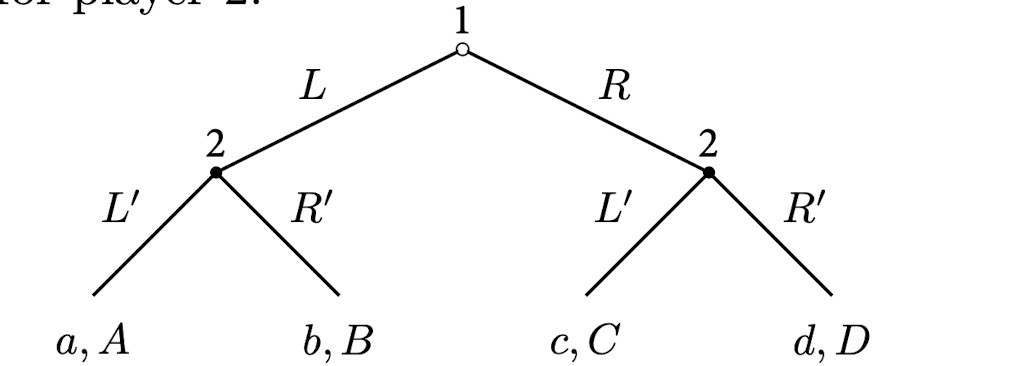
Example
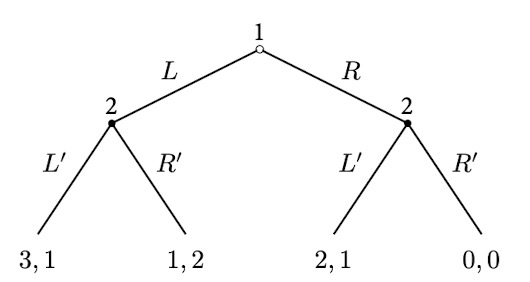
- Player 1 has 2 actions (and also 2 strategies): L and R. Player 2 has 2 actions: L′ and R′, but 4 strategies:$$(L^\prime, L^\prime); (L^\prime, R^\prime); (R^\prime, L^\prime); (R^\prime, R^\prime)$$
- For example, the strategy $(L^\prime, R^\prime)$ means:
- if player 1 plays L, then player 2 plays $L^\prime$;
- if player 1 plays R, then player 2 plays $R^\prime$.
Subgame-perfect Nash Equilibrium
Question: how to represent this game in normal form?

$L^\prime L^\prime$ $L^\prime R^\prime$ $L^\prime L^\prime$ $L^\prime L^\prime$ L 3,1 3,1 1,2 1,2 R 2,1 0,0 2,1 0,0 - there are two NE: $(L, R^\prime R^\prime)$, $(R, R^\prime L^\prime)$
Interpret
- NE $(R, R^\prime L^\prime)$ seems okay. It respects the spirit of backwards induction.
- NE $(L, R^\prime R^\prime)$ has a problem: No matter which action is chosen by Player 1, player 2 must choose L′ at the right node.
- Interpretation: Player 2 tells player 1: if you choose R, I will choose R′ (threat), then each of us will get 0.
- This threat is non-creditable: Player 1 should not believe that player 2 will choose R′ after observing R.
- Key: Ignorance of dynamic feature.
Subgame
Defination
A subgame (子博弈) in an extensive-form game
- begins at a decision node n that is a singleton information set (but is not the game’s initial node);
- includes all the decision and terminal nodes following node n in the game tree (but no nodes that do not follow n);
- does not cut any information sets (i.e., if a decision node n′ follows n in the game tree, then all other nodes in the information set containing n′ must also follow n, and so must be included in the subgame).
- 只能从一个singleton的decision node节点切出来,并且不能把任何information set切断
When focus on a subgame, we shall only consider the relevant part of the strategy profile s.
Relevant part of s specifies the “complete” plans (or strategy profile) for the players in that subgame.
Example
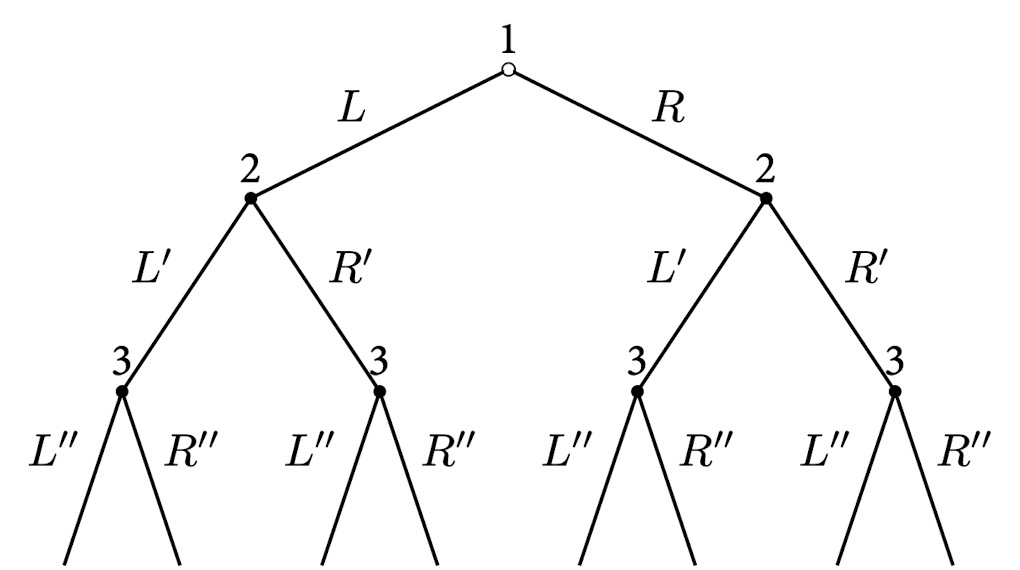
- We have a strategy profile $\left(L,\left(L^{\prime}, R^{\prime}\right),\left(L^{\prime \prime}, R^{\prime \prime}, R^{\prime \prime}, L^{\prime \prime}\right)\right)$.
- We turn to the subgame beginning at player 2’s right decision node.
- The relevant part is $\left(R^{\prime},\left(R^{\prime \prime}, L^{\prime \prime}\right)\right)$ or $\left(-, R^{\prime},\left(R^{\prime \prime}, L^{\prime \prime}\right)\right)$. It is a strategy profile for this subgame.
- We can discuss whether it is “reasonable”, within this subgame.
- One can repeat this procedure for every subgame.
Subgame-Perfect Nash Equilibrium
Definition
A Nash equilibrium is subgame-perfect (子博弈精炼), or is said to be a subgame-perfect Nash equilibrium (子博弈精炼均衡) if the players’ strategies constitute a Nash equilibrium in every subgame.
Application
- It can be shown that any finite dynamic game of complete information has a subgame-perfect Nash equilibrium, perhaps in mixed-strategies.
- To find subgame-perfect Nash equilibria,
- we first need to find Nash equilibria in each subgame,
- then use backwards-induction to solve for the whole game
- Subgame-perfect Nash equilibrium is closely related to two previous concepts:
- 1 backwards-induction outcome;
- 2 subgame-perfect outcome.
- 两者仅存在术语的差别,没有什么本质区别;混用没有问题。
- What’s the diference between an equilibrium and an outcome?
- An equilibrium is a collection of players’ strategies (strategy profile), while an outcome is a collection of players’ actions.
Equilibrium vs. Outcome
- Example:
- The backwards-induction outcome is $\left(a_1^*, R_2\left(a_1^*\right)\right)$.
- The subgame-perfect Nash equilibrium is $\left(a_1^*, R_2(\cdot)\right)$.
- Note that $R_2\left(a_1^*\right)$ is an action, while $R_2(\cdot)$ is a strategy for player 2.
- In Example 1:
- $\left(R, L^{\prime}\right)$ is the backwards-induction outcome,
- while $\left(R,\left(R^{\prime}, L^{\prime}\right)\right)$ is the subgame-perfect Nash equilibrium.
- In the Stackelberg model:
- The backwards-induction outcome is $(q_1^*, q_2^*)$ , where $q_1^*=\frac{a-c}{2}$ and $q_2^*=\frac{a-c}{4}$,
- while the subgame-perfect Nash equilibrium is $\left(q_1^*, R_2\left(q_1\right)\right)$, where $R_2\left(q_1\right)=\frac{a-c-q_1}{2}$.
- For the two-stage game of complete but imperfect information
- Then the subgame-perfect outcome is
$$(a_1^*, a_2^*, a_3^*(a_1^*, a_2^*), a_4^*(a_1^*, a_2^*)) .
$$
- The subgame-perfect Nash equilibrium is$$(a_1^*, a_2^*, a_3^*(a_1, a_2), a_4^*(a_1, a_2)) .$$
- Then the subgame-perfect outcome is
Nash Equilibrium vs. Subgame-Perfect Nash Equilibrium
A Nash equilibrium may not be subgame-perfect.
- Following the example above.
- The Nash equilibrium $\left(R,\left(R^{\prime}, L^{\prime}\right)\right)$ is subgame-perfect, because $R^{\prime}$ and $L^{\prime}$ are the optimal strategies in the left and right subgames, respectively, where player 2 is the only player.
- On the other hand, the Nash equilibrium $\left(L,\left(R^{\prime}, R^{\prime}\right)\right)$ is not subgame-perfect, because when player 1 chooses $R, R^{\prime}$ is not optimal to player 2 in the right subgame, i.e., $R^{\prime}$ is not a Nash equilibrium in that subgame.
- One can think the strategy $\left(R^{\prime}, R^{\prime}\right)$ by player 2 as a threat to player 1.
- Nash equilibria that rely on non-credible threats or promises can be eliminated by the requirement of subgame perfection.
- Subgame-perfect Nash equilibrium is a refinement of Nash equilibrium, i.e.,
${ \text{Subgame-perfect Nash equilibria} } \subseteq{ \text{Nash equilibria} }$
Summary
- We have considered dynamic games of complete information.
- Two basic questions:
- How to describe a dynamic situation $\rightarrow$ extensive-form representation.
- How to solve a dynamic game? Why to introduce SPNE?
- Backwards induction vs. SPNE.
- 静态场景 $\rightarrow$ 静态模型 $\rightarrow$ 标准式
- 静态场景 $\rightarrow$ 动态模型 (带有不完美信息) $\rightarrow$ 扩展式 (没有失去场景的特点)
- 动态场景 $\rightarrow$ 动态模型 $\rightarrow$ 扩展式
- 动态场景 $\rightarrow$ 静态模型 $\rightarrow$ 标准式 (失去场景的动态特点)
L4:Repeated games
- In a long-term relationship, one must consider how his/her current behavior will influence others’ behavior in the future, or how threats or promises about future behavior can afect current behavior.
- In these dynamic situations, one might care about “reputation”, which is often used to describe how a person’s past actions affect future beliefs and behavior.
Finitely repeated games
- The payoff of each player in the whole game is simply the sum of two payoffs in both stages (i.e., no discounting).
Definition
- Let $G = ⟨A1 , . . . , An; u1, . . . , un⟩$ denote a static game of complete information in which players 1 through n simultaneously choose actions $a_1$ through an from the action spaces $A_1$ through $A_n$, and the payoffs are $u_1(a_1, . . . , a_n)$ through $u_n(a_1, . . . , a_n)$.
- The game G is called the stage game (阶段博弈) of the repeated game.
- Given a stage game G, let $G(T)$ denote the finitely repeated game in which G is played T times, with the outcomes of all preceding plays observed before the next play begins. The payoffs for $G(T)$ are simply the sum of the payoffs from the T stage games.
Proposition
- If the stage game G has a unique Nash equilibrium, then for any finite T, the repeated game $G(T)$ has a unique subgame-perfect outcome: the Nash equilibrium of G is played in every stage.
- if the stage game G has multiple Nash equilibria:
- there may be subgame-perfect outcomes of the repeated game $G(T)$ in which, for any t < T, the outcome of stage t is not a Nash equilibrium of G.
- 可以达到整体的更优化,因为可以用差的NE作为威胁。
Infinitely repeated games
Definition
- Given a stage game G, let $G(∞, δ)$ denote the ininitely repeated game in which G is played forever and players share the discount factor $δ$.
- For each t, the outcomes of the t − 1 preceding plays are observed before the t-th stage begins.
- Each player’s payoff in $G(∞, δ)$ is the present value of the player’s payoffs from the infinite sequence of stage games.
Strategies
- noncooperative strategy:
- play one choice in every stage.
- (grim) trigger strategy (触发策略):
- play A in the first stage; in stage t, if the outcome of all t − 1 preceding stages has been the binding choice, then play A; otherwise, play B.
- tit-for-tat (or tit for two tats) strategy (以牙还牙策略)
- carrot-and-stick strategy (or two-phase strategy) (胡萝卜加大棒策略)
Nash Equilibria
- 需要证明所有偏离的策略收益都不如现在的选择。
Subgame-perfect Nash Equilibria
In an infinitely repeated game, a subgame is characterized by its previous history. The subgames can be grouped as follows:
- Subgames whose previous histories are always a finite sequence of binding choice.
- 此时,判断是否要deviate。
- Subgames whose previous histories contain other outcomes different from the binding choice.
- 此时,选择NE是均衡
- Subgames whose previous histories are always a finite sequence of binding choice.
需要证明在每一个情况都是NE
$\color{red}{\text{One-deviation principle (单阶段偏离原则)}}$
- A strategy profile is a subgame-perfect Nash equilibrium if and only if, for each player i and for each subgame, no single deviation would raise player i’s payoff in the subgame.
Two-phase strategy SPNE
- 胡萝卜加大棒策略
- in the first period, produce half of the monopoly quantity $q_m/2$. In period t, produce $q_m/2$ if both firms produce $q_m/2$ or both firms produce x in period t − 1; otherwise, produce x.
- This strategy involve a (one-period) punishment phase in which the firm produces x and a (potentially infinite) collusive phase in which the firm produces $q_m/2$
- Such a strategy punishes
- a firm for deviating from the collusive phase;
- a firm for deviating from the punishment phase.
Folk theorem
Definition
- Cooperative equilibria which do not exist in static games can be achieved in repeated games.
Friedman Theorem
Feasible Payoff
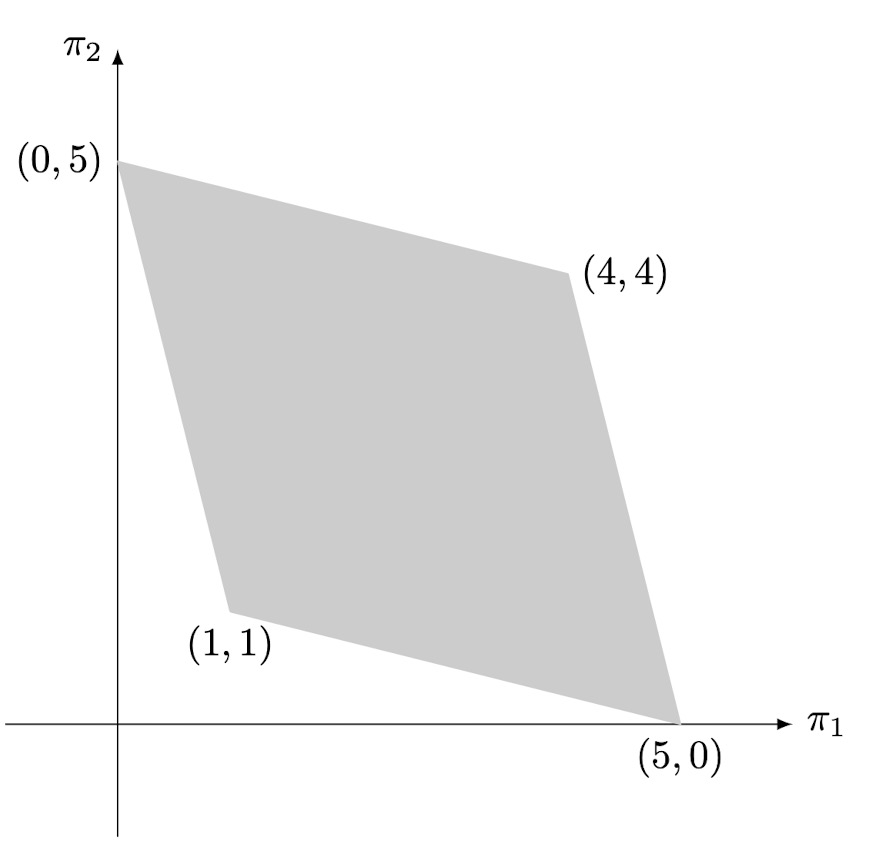
- The payoffs $(x_1 , . . . , x_n)$ are feasible in the stage game G if they are a convex combination (i.e., a weighted average, where the weights are all nonnegative and sum to one) of the pure-strategy payoffs of G.
Average Payoff
- Given the discount factor $\delta$, the average payoff of the infinite sequence of payoffs $\pi_1, \pi_2, . . .$ is
- $$(1-\delta )\sum_{i=1}^\infty \delta^{(t-1)}\pi_t$$
- Both present value and average payoff can present a player’s payoff in an infinitely repeated game.
- Average payoff is directly comparable to the payoffs from the stage game.
Friedman Theorem
- Let G be a finite, static game of complete information. Let $(e_1,…,e_n)$ denote the payoffs from a Nash equilibrium of G, and let $(x_1,…, x_n)$ denote any feasible payoffs from G, where $x_i > e_i$ for each player i. If the discount factor $\delta$ is suiciently close to one, then there exists a subgame-perfect Nash equilibrium in the infinitely repeated game G( ∞, δ) that achieves $(x_1,…, x_n)$ as the average payoff.
L5:Static games with incomplete information
Intro
- games of complete information, i.e., each player’s payoff function is common knowledge among all players.
- In the auction example, each player’s payoff function is no longer common knowledge:
- Buyer i’s payof function contains private information, which is not known by other buyers.
- This is an example of incomplete information games (不完全信息博弈), in which at least one player is uncertain about another player’s payoff function.
- Games of incomplete information are also called Bayesian games (贝叶斯博弈)
- Two types of Bayesian games: static vs. dynamic.
Cournot Competition under Asymmetric Information
- 类似与原本的古诺模型,但是现在firm2的成本 $c_2$ 有 $\theta$ 的可能性是 $c_H$ , 有 $1-\theta$ 的可能性是 $c_L$
- 因此,信息不对称:
- Firm 1’s cost function is known by both firms.
- $c_1$ is common knowledge.
- Firm 2’s cost function is completely known by itself, but not known by firm 1.
- $c_2$ is not common knowledge.
- Firm 1 only knows the distribution of firm 2’s marginal cost
- Firm 1’s cost function is known by both firms.
- 自然,firm 2会对于不同的成本选择不同的生产量
- firm 1 应该合理预期这种差异
- Let $q_2^*(c_H)$ and $q_2^*(c_L)$ denote firm 2’s quantity choices when its marginal cost is $c_H$ and $c_L$ respectively, and let $q^∗_1$ denote firm 1’s single choice of quantity.
- If firm 2’s cost is $c_j (j = L, H)$, it will choose $q^∗_2(c_j)$ to solve
- $$\max_{q_2}(a-q1^*-q_2-c_j)q_2$$
- firm 1 chooses $q^∗_1$ to solve
- $$\max_{q_1}\theta(a-q_2^*(c_H)-q_1-c)q_1+(1-\theta)(a-q_2^*(c_L)-q_1-c)q_1$$
- 一阶导数:
- $$q_2^*(c_H) =\frac{a-q_1^*-c_H}{2}$$
- $$q_2^*(c_L)=\frac{a-q_1^*-c_L}{2}$$
- $$q_1^* =\frac{a-\theta q_2^*(c_H)-(1-\theta) q_2^*(c_L)-c}{2}$$
- The equilibrium of this game is $(q_1^*,(q_2^*(c_H), q_2^*(c_L)))$, where
- $$q_1^* =\frac{a-2 c+\theta c_H+(1-\theta) c_L}{3}$$
- $$q_2^*(c_H) =\frac{a-2 c_H+c}{3}+\frac{1-\theta}{6}\left(c_H-c_L\right)$$
- $$q_2^*(c_L)=\frac{a-2 c_L+c}{3}-\frac{\theta}{6}(c_H-c_L)$$
- We know $q_2^*(c_H)<q_2^*(c_L) \Rightarrow$ firm 2 produces less when its marginal cost increases.
- Firm 2 knows firm 1’s payoff function, while firm 1 does not know firm 2’s payoff functions but only knows the probability distribution.
- This is Bayesian game.
Static Bayesian games
- Consider a general static Bayesian game.
- Let player $i$ ‘s possible payoff function be $u_i\left(a_1, \ldots, a_n ; t_i\right)$, where $a_i$ is player $i$ ‘s action and $t_i$ is called player $i$ ‘s type (类型), which belongs to a set of possible types $T_i$ (or type spaces).
- Player $i$ ‘s type $t_i$ is his private information, and each type $t_i$ corresponds to a different payoff function of player $i$.
- Let $t_{-i}=\left(t_1, \ldots, t_{i-1}, t_{i+1}, \ldots, t_n\right)$ be the types of other players and $T_{-i}$ be the set of all $t_{-i}$.
- Player $i$ is uncertain about other players’ types, but only knows the probability distribution $p_i\left(t_{-i} \mid t_i\right)$ on $T_{-i}$, which is i’s belief (猜测/估计/信念) about other players’ types, given i’s knowledge of his own $t_i$.
Definition
- The normal-form (标准式) representation of an $n$-player static Bayesian game specifies players’
(1) action spaces $A_1, \ldots, A_n$,
(2) type spaces $T_1, \ldots, T_n$,
(4) payoff functions $u_1, \ldots, u_n$. - We denote this game by
$$
G=\left\langle A_1, \ldots, A_n ; T_1, \ldots, T_n ; p_1, \ldots, p_n ; u_1, \ldots, u_n\right\rangle
$$
Example
- In the Cournot game with asymmetric information,
- $A_{\ell}=A_2=[0, \infty)$
- $T_1={c}$, and $T_2={c_H, c_L}$
- 至少是singleton
- $p_1\left(c_H \mid c\right)=\theta, p_1\left(c_L \mid c\right)=1-\theta$, and $p_2\left(c \mid c_H\right)=p_2\left(c \mid c_L\right)=1$
- Payoff functions are
$$
\begin{aligned}
\pi_1\left(q_1, q_2 ; c\right) & =\left(a-q_1-q_2-c\right) q_1 \\
\pi_2\left(q_1, q_2 ; c_L\right) & =\left(a-q_1-q_2-c_L\right) q_2 \\
\pi_2\left(q_1, q_2 ; c_H\right) & =\left(a-q_1-q_2-c_H\right) q_2
\end{aligned}
$$
timing
- The timing of a static Bayesian game:
- Nature draws a type vector $t = (t_1 ,…, t_n)$, where $t_i ∈ T_i$ ;
- Nature reveals $t_i$ to player i, but not to any other players;
- The players simultaneously choose actions, player i choosing $a_i ∈ A_i$;
- Payoffs $u_i (a_1 ,…, a_n;t_i)$ are received.
- By introducing the frictional moves by nature in 1 and 2, we have described a game of incomplete information as a game of imperfect information.
Bayes’ rule
- We often assume that the nature draws $t=\left(t_1, \ldots, t_n\right)$ according to the prior probability distribution $p(t)$ (先验概率分布/事前概率分布), which is common knowledge.
- Then the posterior belief $p_i\left(t_{-i} \mid t_i\right)$ can be computed by Bayes’ rule 贝叶斯公式
$$
p_i\left(t_{-i} \mid t_i\right)=\frac{p\left(t_{-i}, t_i\right)}{\sum_{t_{-i}^{\prime} \in T_{-i}} p\left(t_{-i}^{\prime}, t_i\right)} .
$$
Remarks
- First, there are games in which player i has private information not only about his or her own payoff function but also about another player’s payoff function. We write player i’s payoff function as $u_i (a_1 , . . . , a_n; t_1, . . . , t_n)$. (interdependent (相互决定))
- Second, we typically assume that players’ types are independent (otherwise, correlated), i.e., $p_i(t_{−i} |t_i)$ does not depend on $t_i$, which can be denoted by $p_i(t_{−i})$. But $p_i(t_{−i})$ is still derived from the prior distribution $p(t)$.
Strategy and Bayesian Nash equilibrium
- In the static Bayesian game $G = ⟨A_1 , . . . , A_n; T_1, . . . , T_n; p_1, . . . , p_n; u_1, . . . , u_n⟩$, a strategy for player i is a function $s_i(t_i)$, i.e., $s_i: T_i → A_i$. For given type $t_i$, $s_i(t_i)$ gives an action of player i. Player i’s strategy space $S_i$ is the set of all functions from $T_i$ into $A_i$.
- 在上例中,$(q^*_2(c_H),q^*_2(c_L))$ 是player 2 的一个策略,$q^*_1$ 是player 1 的一个策略
Definition
- In the static Bayesian game
- $G=\langle A_1, \ldots, A_n ; T_1, \ldots, T_n ; p_1, \ldots, p_n ; u_1, \ldots, u_n\rangle$, the strategy profile $s^*=(s_1^*, \ldots, s_n^*)$ are a (pure-strategy) Bayesian Nash equilibrium (贝叶斯-纳什均衡) if for each player $i$ and for each of $i$ ‘s types $t_i \in T_i, s_i^*\left(t_i\right)$ solves
- $$\max_{a_i \in A_i} \sum_{t_{-i} \in T_{-i}} u_i(s_{-i}^*(t_{-i}), a_i ; t_i) \cdot p_i(t_{-i} \mid t_i)$$
- 先验分布下不同情况的收益加权。
- In a general finite static Bayesian game (finite players, finite actions, and finite types), a Bayesian Nash equilibrium exists, perhaps in mixed strategies.
- In a Bayesian Nash equilibrium, each player’s strategy is a best response to other players’ strategies.
- In other words, no player wants to change his or her strategy unilaterally given other players’ equilibrium strategies, even if the change involves only one action by one type.
- A Bayesian Nash equilibrium is simply a Nash equilibrium in a Bayesian game.
Application
A trading game
- 可以把带有概率的game转化成多个人,每个人代表一种possibility
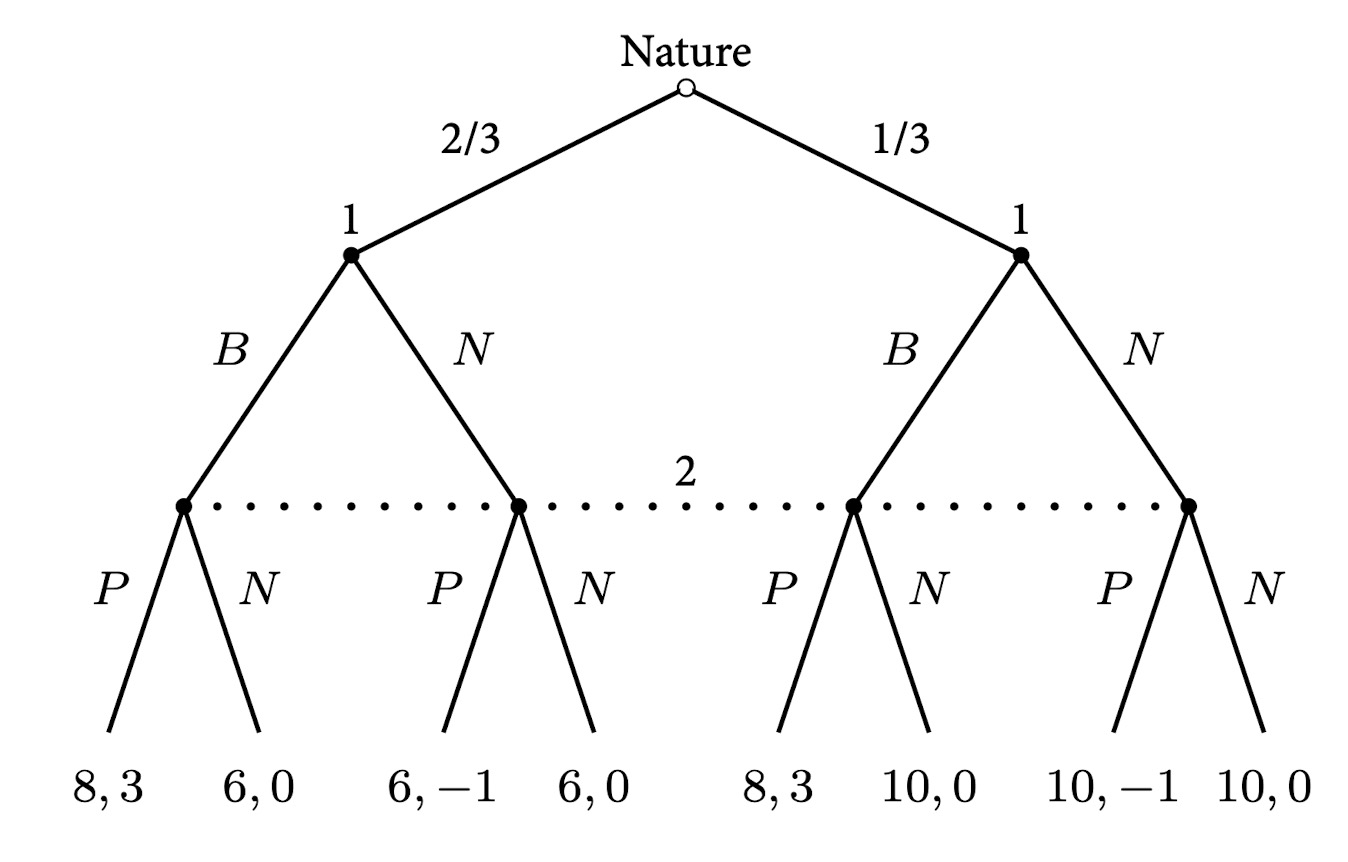
- Normal-form representation of the game:
- Action spaces: A1 = {B, N} and A2 = {P, N};
- Type spaces: T1 = {10, 14} and T2 = {1};
- Beliefs:the buyer’s belief on the seller’s type is 1 on type 1, the seller’s belief on the buyer’s types is 2/3 on 10 and 1/3 on 14;
- Payoffs are given as above.
- Strategy spaces: S1 = {BB, BN, NB, NN} and S2 = {P, N}
- The meaning of BN: the buyer with outside option 10 chooses “to buy” and with outside option 14 chooses “not to buy”.
- 可以用bi-matrix来表示这个状态,找到best response
Mixed strategies revisited
考虑 battle of sexes
Suppose the couple are uncertain about the payoffs for each other
Opera Football Opera 1,2+$t_w$ 0,0 Football 0,0 2+$t_h$, 1 Here $t_w$ is privately known by the wife, while $t_h$ is privately known by the husband.
Assume that $t_w$ and $t_h$ are independently drawn from a uniform distribution on $[0, x]$, where x > 0.
The normal-form representation of this static Bayesian game is $G=\left\langle A_h, A_w ; T_h, T_p ; p_h, p_w ; u_h, u_w\right\rangle$ :
- $A_h=A_w={ \text{Opera, Football} }$;
- $T_h=T_w=[0, x]$
- The husband believes that $t_w$ (the wife believes that $t_h$ ) is uniformly distributed on $[0, x]$;
- $u_h$ and $u_w$ are given before.
- 构造两个 critical value, $\bar{t_w}$ 和 $\bar{t_h}$
- In the Bayesian Nash equilibrium, the husband will choose Football if $t_h$ exceeds the critical value $\bar{t_h}$, and choose Opera otherwise.
- 老婆同理
解
- Given the wife’s strategy, the husband’s expected payoffs of choosing Opera and Football are
$$
\begin{aligned}
u_h\left(\text { Opera, } s_w^* \mid t_h\right) & =\operatorname{Pr}\left(s_w^*=\text { Opera }\right) \cdot 1+\operatorname{Pr}\left(s_w^*=\text { Football }\right) \cdot 0 \\
& =\left(1-\frac{\bar{t}_w}{x}\right) \cdot 1+\frac{\bar{t}_w}{x} \cdot 0=1-\frac{\bar{t}_w}{x},
\end{aligned}
$$
and
$$
u_h\left(\text { Football, } s_w^* \mid t_h\right)=\left(1-\frac{\bar{t}_w}{x}\right) \cdot 0+\frac{\bar{t}_w}{x} \cdot\left(2+t_h\right)=\frac{\bar{t}_w}{x}\left(2+t_h\right) .
$$ - Thus, choosing Opera is optimal iff
$$
1-\frac{\bar{t}_w}{x} \geq \frac{\bar{t}_w}{x}\left(2+t_h\right) \Longleftrightarrow t_h \leq \frac{x}{\bar{t}_w}-3=\bar{t}_h .
$$
- wife 同理
- $$1-\frac{\bar{t}_h}{x} \geq \frac{\overline{\bar{t}}_h}{x}\left(2+t_w\right) \Longleftrightarrow t_w \leq \frac{x}{\bar{t}_h}-3=\bar{t}_w .$$
- Solving simultaneously, we obtain $\bar{t}_h$ and $\bar{t}_w$ satisfy
$$
t^2+3 t-x=0 .
$$
- Thus, $\bar{t}_h=\bar{t}_w=\frac{\sqrt{9+4 x}-3}{2}$.
- In equilibrium, the husband plays Opera with probability $p^*$ and Football with probability $1-p^*$, while the wife plays Football with probability $p^*$ and Opera with probability $1-p^*$, where
$$
p^*=\frac{\bar{t}_h}{x}=\frac{\bar{t}_w}{x}=\frac{2}{\sqrt{9+4 x+3}} .
$$ - When $x \rightarrow 0$, we get that $p^* \rightarrow \frac{1}{3}$.
- As the incomplete information disappears, the players’ behavior in this pure-strategy Bayesian Nash equilibrium approaches their behavior in the mixed-strategy Nash equilibrium in the original game of complete information.
L6: Auction
Intro
- An auction is a mechanism of allocating goods.
- Analyze bidders’ behaviors.
- Analyze auctioneer’s “optimal” choice.
- Advantages of auctions:
- a simple way of determining the market-based prices;
- more flexible than setting a fixed price;
- can usually achieve eiciency by allocating the resources to those who value them most highly.
Types of auctions
- Number of objects
- A single object or many?
- Open vs. sealed-bid
- Do you know the bids of other participants?
- One-sided vs. two-sided
- Do buyers and sellers both submit bids, or just buyers?
- Private value vs. common value
- Do the bidders have the same valuation for the object?
Second-price auction
- 每个人的心理预期是从一个分布中随机的,$F_i(·)$
- 每个人都只知道自己的心理预期但不知道别人的
- 所有人同时竞价
- 出价最高者赢得物品,并支付第二高价格
- 如果同时好几个人出价最高,则随机给到一个人
结论
- For each player i, the strategy of bidding his valuation (i.e., $s^∗_i(v_i) = v_i$ )weakly dominates all other strategies.
- 分别考虑报价更低与更高,都是 weakly dominates
First-price auction
两个bidder,valuation在(0,1)上服从uniform distribution
只知道自己的valuation
同时bid
出价高者得,出价低者不用出钱
出价相同,随机获得
Normal-form representation of this static Bayesian game $G=\left\langle A_1, A_2 ; T_1, T_2 ; p_1, p_2 ; u_1, u_2\right\rangle$
- $A_1=A_2=[0, \infty)$, and each bid is $b_i \in A_i$;
- $T_1=T_2=[0,1]$, and each valuation is $v_i \in T_i$;
- Player $i$ believes that $v_j$ is uniformly distributed on $[0,1]$;
- The payoff $u_i\left(b_i, b_j ; v_i\right)$ is
- $$u_i(b_i, b_j ; v_i)= \begin{cases}v_i-b_i, & \text { if } b_i>b_j \\ \frac{1}{2}(v_i-b_i), & \text { if } b_i=b_j \\ 0, & \text { if } b_i<b_j\end{cases}$$
- Bidder $i$ ‘s strategy is a function $b_i(v_i)$ from $[0,1]$ to $[0, \infty)$.
- $(b_1^*(v_1), b_2^*(v_2))$ is a Bayesian Nash equilibrium if and only if for each player $i$ and each type $v_i \in[0,1], b_i^*\left(v_i\right)$ solves
- $$\begin{aligned}
& \max {b_i \geq 0} \mathbf{E}{v_j} u_i(b_i, b_j^*(v_j) ; v_i) \\
= & \max _{b_i \geq 0}{(v_i-b_i) Prob[b_i>b_j^*(v_j)]+\frac{v_i-b_i}{2} Prob[b_i=b_j^*(v_j)]} \end{aligned}$$
Linear Bayesian NE
- 可能会有许多纳什均衡,现在只考虑线性情况
- $b^*_1(v_1)=a_1+c_1v_1$ , $b^*_2(v_2)=a_2+c_2v_2$
- 需要找到对应的a和c
- 理性:
- a小于1,不然收益永远为负
- c大于等于0,随着valuation上升,出价也上升
- a大于等于0,出价不能为负
- 当 $b_j$ 是线性的时候,$Prob(b_i=a_j+c_jv_j)=Prob(v_j=\frac{b_i-a_j}{c_j})=0$
- 对于任意的v,需要
- $$\max_{b_i\geq 0}(v_i-b_i)Prob(v_j<\frac{b_i-a_j}{c_j})$$
- Since $b_j^*\left(v_j\right)=a_j+c_j v_j \in\left[a_j, a_j+c_j\right]$, we can restrict our attention to $b_i \in\left[a_j, a_j+c_j\right]$
- i.e., $b_i<a_j$ is pointless, while $b_i>a_j+c_j$ is not rational
- Under the above restriction, we know
$$
0 \leq \frac{b_i-a_j}{c_j} \leq 1
$$ - Player $i$ s best response solves
$$
\max _{a_j \leq b_i \leq a_j+c_j}\left(v_i-b_i\right) \frac{b_i-a_j}{c_j}
$$
- FOC implies the potentially optimal choice is $b_i^o=\frac{v_i+a_j}{2}$.
- 即求导
- It is the optimal choice iff $b_i^o=\frac{v_i+a_j}{2} \in\left[a_j, a_j+c_j\right]$
- 即 $a_j \leq v_i \leq a_j+2 c_j$.
- The best response function of bidder $i$ is
$$
b_i\left(v_i\right)= \begin{cases}a_j, & \text { if } v_i \leq a_j \\ \frac{1}{2}\left(v_i+a_j\right), & \text { if } a_j<v_i \leq a_j+2 c_j \\ a_j+c_j, & \text { if } v_i>a_j+2 c_j .\end{cases}
$$
- We want the equilibrium bid $b_i\left(v_i\right)$ to be a linear function on $[0,1]$.
- There are three cases:
- $$[0,1] \subseteq\begin{cases}(-\infty, a_j] \\
{[a_j, a_j+2 c_j]} \\
{[a_j+2 c_j, \infty)}
\end{cases}$$- 第一种情况不满足a小于1
- 第三种情况不满足c大于0
- 因此只能是第二种情况,$b_i=\frac{v_i+a_j}{2}$
- In a Bayesian Nash equilibrium,$$b_i^*\left(v_i\right)=a_i+c_i v_i=\frac{1}{2}\left(v_i+a_j\right)$$for all $v_i \in[0,1]$.
- Then we have$$a_i=\frac{1}{2} a_j, \text { and } c_i=\frac{1}{2}$$for $i, j=1,2$ and $i \neq j$.
- Therefore,
$$
a_1=a_2=0, \text { and } c_1=c_2=\frac{1}{2} .
$$ - The unique linear Bayesian Nash equilibrium is$$b_1^*(v_1)=\frac{1}{2} v_1, \text { and } b_2^*(v_2)=\frac{1}{2} v_2$$
- 如果能直接猜出这个解,就可以直接验证。